Е. Расчет шпунтовых ограждений

- Шпунтовые стенки рассчитывают по первой группе предельных состояний;

- Подавляющее большинство методов основано на классической теории предельного равновесия грунтов (E_a, E_п, E_о)

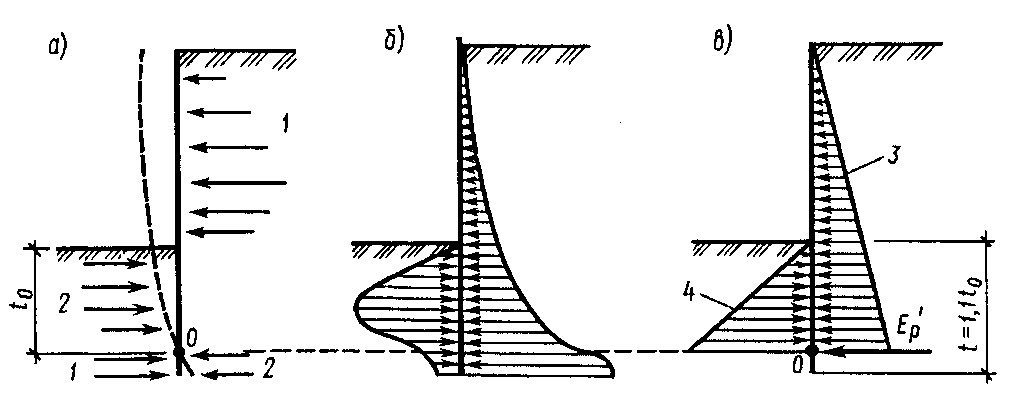
Рис. 14.6. Работа безанкерной шпунтовой стенки:

а – действующие силы; б – фактическая эпюра давления грунта; в – эпюра давления грунта, принятая в расчете; 1 – активное давление; 2 – пассивное давление; 3 – предельное активное давление; 4 – предельное пассивное давление.

→ Безанкерные шпунтовые стенки (рис. 14.6)

Задача состоит в определении глубины ее забивки, усилий, действующих в стенках, и размеров поперечного сечения шпунта.

- Принимается, что под действием E_a, стенка стремится повернуться вокруг т.О, расположенной на некоторой глубине t_o ниже дна котлована

- Устойчивость стенки обеспечивается вследствие уравновешенного активного и пассивного давления грунта с разных ее сторон.

- За счет перемещений и гибкости стенки получается довольно сложным криволинейная эпюра давлений грунта на стенку (рис. 14.6. б)

- С целью упрощения расчета эта эпюра заменяется на более простую (рис. 14.6. в). После этого задача становится статически определимой с двумя неизвестными t_o и E_р’, которые находятся из уравнений равновесия.

равновесие момента относительно т. О

∑М_т.о.=0 следовательно приводит к уравнению 3^й степени относительно t_o; t_o

будучи определена, позволяет найти E_р’ из ∑X=0 – уравнение равновесия горизонтальных сил.

- Поскольку полученная t_o определена из условия предельного состояния, для обеспечения запаса, ее увеличивают на величину ∆t

полная глубина заделки шпунтовой стенки ;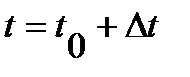

∆t определяется из условия реализации обратного отпора грунта E_р’

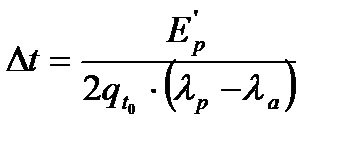
где q_to – вертикальное давление грунта на глубине приложенной силы E_р’

λ_р, λ_а – коэффициент активного и пассивного давления грунта

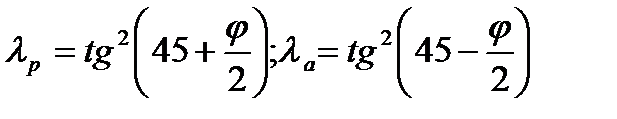
- На практике чаще всего составляется только одно уравнение моментов, не содержащее E_р’, и определяется t_o, а полная заделка шпунтовой стенки в грунт принимается равной

→ Анкерные шпунтовые стенки

- В зависимости от жесткости стенки различают 3 расчетные схемы:

· свободно опертая стенка (схема Ю.К.Якоби)

· заделанная стенка (схема Блюма-Ломейера)

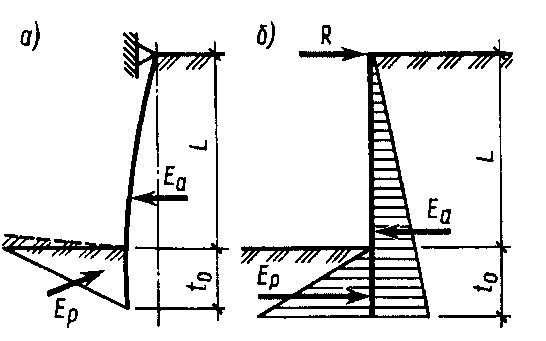
Рис. 14.7. Расчет заанкеренной стенки схеме Э.К.Якоби:

а – схема работы стенки; б – расчетная схема

Критерий жесткости шпунтовой стенки определяется отношением:

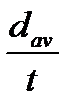
d_av – приведенная высота стенки

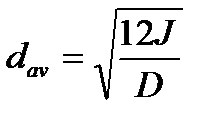
J – момент инерции приведенного сечения стенки «М»

D – ширина шпунтины, м;

t – глубина заложения стенки, м.

- При 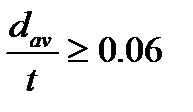- стенка повышенной жесткости (ж/б стена или стенка из буронабивных свай) ее следует рассчитывать по схеме «свободного опирания».

→ Свободно опертая стенка (схема Э. К. Якоби)

- Расчет исходит из предположений, что в момент потери устойчивости стенка под действием сил активного давления грунта E_a, будет поворачиваться вокруг точки крепления анкера (рис. 14.7 а). При этом на дне котлована возникает выпор грунта и реакция массивного давления

Упрощенная расчетная схема – рис.14.7. б

- Необходимо найти:

- t_o,- длина заделки стенки;

- R - усилия в стенке и в анкере;

- подобрать сечение стенки и анкера.

· Приняв т.О (точка крепления анкера) – неподвижной t_o и R определяют из уравнений равновесия:

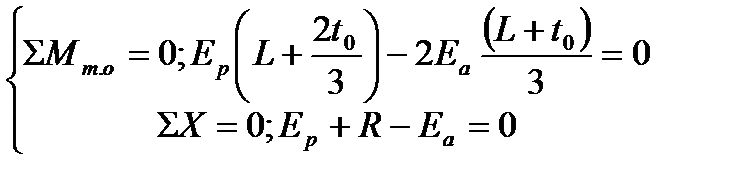
За расчетное значение заделки принимают

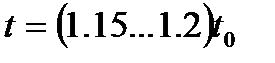
→ Заделанная стенка (схема Биома-Ломейера) или (метод упругой линии)

· Расчет ведется в предположении, что нижний участок забитой части стенки полностью защемлен в грунте.

· Упрощенная диаграмма строится по аналогии т.О расположена на расстоянии 0,2t_o от нижнего конца стенки (рис. 14.8)

· Задача статически неопределенна, т.к. содержит три неизвестные:

t ; R; Усилие в анкере; и E_р

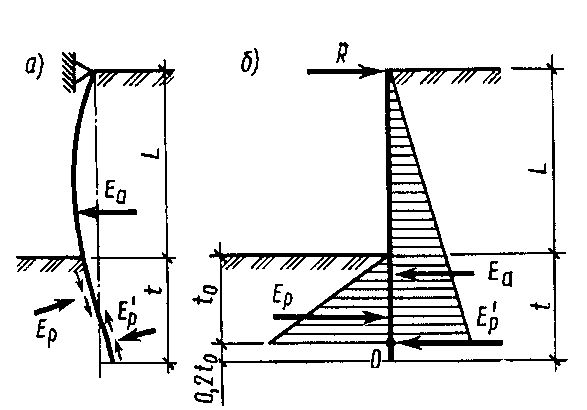
Рис. 14.8. Расчет заанкерной стенки по схеме Блюма-Ломейера:

а – схема работы стенки; б – расчетная схема.

Необходимо помимо уравнений равновесия добавочное условии – это равенство …угла поворота защемленного участка в месте заделки стенки, т.е. в т. О

- Решение ведется методом последовательных приближений.

1. Задаемся t_o - глубиной заделки, определяем t

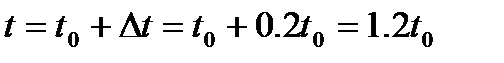
2. Из уравнение равновесия находим R и E_р’

3. Строим эпюру изгибающих моментов выше т.О

4. Путем двойного интегрирования составленного уравнения моментов получаем уравнение упругой линии стенки.

(Две постоянные интегрирования определяются из условия, что точка анкеровки и т.О являются неподвижными)

5. Из уравнения упругой линии стенки определяют угол ее поворота в т.О

Если угол θ≠0, то изменяем глубину t_o и производим действия п.п 1-5 заново.

6. Дальнейший расчет заключается в построении эпюры изгибающих моментов и определении М_мах, по которому проверяют сечение шпунта.

- Объем вычислений можно существенно сократить если использовать графоаналитический метод расчета, изложенный в справочнике проектировщика.