Расчет проводов и тросов на механическую прочность.
3.1 Расчет ветровых и гололедных нагрузок
Для обеспечения надежной работы ВЛ в естественных условиях необходимо учитывать скорость ветра, гололедно-изморозевые отложения и температуры воздуха в районе, где проходит трасса ВЛ. Для определения нагрузок на элементы ВЛ, согласно ПУЭ, принимаются наиболее неблагоприятные сочетания климатических условий, наблюдаемых не реже одного раза в пять лет для линий напряжением до 3 кВ, одного раза в 10 лет для линий напряжением 6-330 кВ и одного раза в 15 лет для линий напряжением 500 кВ и выше. Увеличение периодов повторяемости с ростом напряжения ВЛ объясняется большей ответственностью линий более высокого напряжения.
Расстояние от проводов (или троса) до земли меняется по длине пролета. Поэтому в расчетах используется понятие высоты приведенного центра тяжести проводов (или троса) - 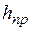 . Величина
. Величина 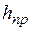 , м, определяется по формуле:
, м, определяется по формуле:
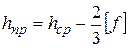 , (3.1)
, (3.1)
где 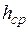 – средняя высота подвеса проводов (или троса) на опоре, м;
– средняя высота подвеса проводов (или троса) на опоре, м;
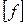 - допустимая стрела провеса провода (или троса), м.
- допустимая стрела провеса провода (или троса), м.
Значение 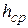 , м, для проводов определяется по формуле:
, м, для проводов определяется по формуле:
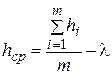 ,
,
где  - расстояние от земли до i-й траверсы опоры, м;
- расстояние от земли до i-й траверсы опоры, м;
m – количество проводов на опоре;
 - длина гирлянды изоляторов, м.
- длина гирлянды изоляторов, м.
Для предварительных расчетов длины гирлянд изоляторов могут быть приняты следующими: для ВЛ 35 кВ – 0,6 м; для ВЛ 110 кВ – 1,3 м; для ВЛ 220 кВ – 2,4 м.
Значение 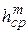 для троса определяется высотой подвеса троса:
для троса определяется высотой подвеса троса:
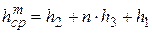 ,
,
где h2, h3, h1 - расстояния по рисунку В1 приложения, м;
n – число цепей.
Допустимая стрела провеса провода, м, определяется по формуле:
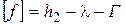 , (3.2)
, (3.2)
где h2 – расстояние от земли до нижней траверсы, м;
 - длина гирлянды изоляторов, м;
- длина гирлянды изоляторов, м;
Г – габаритный размер, м, значения габаритного размера приведены в табл. 2.1.
Допустимая стрела провеса троса, м, определяется по формуле:
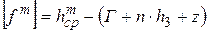 , (3.3)
, (3.3)
где z – наименьшее допустимое расстояние по вертикали между проводом и тросом в середине пролета, м.
Расстояние z определяется ПУЭ в зависимости от расчетной длины пролета (табл. 3.1). Промежуточные значения определяются путем линейной интерполяции.
Таблица 3.1
Длина пролета 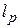 , м , м
| |||||||
| Расстояние z, м | 2,0 | 3,2 | 4,0 | 5,5 | 7,0 | 8,5 | 10,0 |
При определении ветровых нагрузок на провода и тросы ВЛ принято использовать не скорость ветра V , а скоростной напор ветра 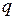 , который определяется по формуле:
, который определяется по формуле:
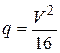 .
.
Скоростной напор ветра представляет собой давление воздуха, движущегося со скоростью V, на один квадратный метр. По величине скоростного напора ветра вся территория бывшего СССР разделена на семь ветровых районов. Для каждого из них в ПУЭ указаны нормативные значения скоростного напора на высоте 15 м от поверхности земли (табл. 3.2).
Таблица 3.2
| Район по ветру | Нормативное значение q, даН/м2, при повторяемости | Поскольку скорость ветра увеличивается с увеличением высоты, то для 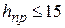 м значения м значения 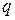 берутся непосредственно из табл. 3.2. При берутся непосредственно из табл. 3.2. При 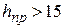 м вводится поправочный коэффициент м вводится поправочный коэффициент 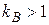 . Значения этого коэффициента приведены в ПУЭ и табл. 3.3. . Значения этого коэффициента приведены в ПУЭ и табл. 3.3.
|
| 1 раз в 5 лет | 1 раз в 10 лет | |
Таблица 3.3
Высота 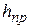 , м , м
| до 15 | 350 и выше | |||||
Коэффициент 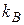
| 1,0 | 1,25 | 1,55 | 1,75 | 2,1 | 2,6 | 3,1 |
Таким образом, максимальное значение скоростного напора ветра определяется так:
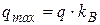 , (3.4)
, (3.4)
где 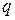 – нормативный скоростной напор ветра из табл. 3.2.
– нормативный скоростной напор ветра из табл. 3.2.
Отложения гололеда, изморози и мокрого снега на проводах и тросах ВЛ имеют различную форму (рис. 3.1а). Эти отложения регистрируются на метеостанциях, взвешиваются и приводятся к эквивалентной массе гололеда круглой цилиндрической формы с плотностью 900 кг/м3 (рис. 3.1б). Толщина стенки С этого цилиндра является исходной величиной для определения интенсивности гололедообразования в данном районе.
 По толщине стенки гололеда вся территория бывшего СССР разделена на четыре района и особый район. В ПУЭ и табл. 3.4 приведены значения нормативной толщины стенки гололеда С для различных районов.
По толщине стенки гололеда вся территория бывшего СССР разделена на четыре района и особый район. В ПУЭ и табл. 3.4 приведены значения нормативной толщины стенки гололеда С для различных районов.
Таблица 3.4
| Район по гололеду | Нормативное значение С, мм, при повторяемости | Для  м значения С берутся непосредственно из табл. 3.4. При м значения С берутся непосредственно из табл. 3.4. При 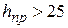 м вводятся поправочные коэффициенты на высоту м вводятся поправочные коэффициенты на высоту 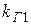 (табл. 3.5) и диаметр провода (или троса) (табл. 3.5) и диаметр провода (или троса) 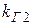 (табл. 3.6). (табл. 3.6).
|
| 1 раз в 5 лет | 1 раз в 10 лет | |
| особый | 20 и более | более 22 |
Таблица 3.5
| Высота hПР, м | до 25 | |||||
| Коэффициент kГ1 | 1,0 | 1,4 | 1,6 | 1,8 | 2,0 | 3,0 |
Таблица 3.6
| Диаметр провода (или троса) d, мм | ||||||
| Коэффициент kГ2 | 1,1 | 1,0 | 0,9 | 0,8 | 0,7 | 0,6 |
Таким образом, максимальное значение толщины стенки гололеда при 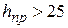 м определяется так:
м определяется так:
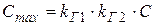 . (3.5)
. (3.5)
Для определения значений 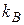 ,
,  из соответствующих таблиц используется метод линейной интерполяции.
из соответствующих таблиц используется метод линейной интерполяции.
Температура окружающей среды сказывается на работе ВЛ путем прямого влияния на степень натяжения и провисания проводов и тросов. При расчетах проводов и тросов на механическую прочность принимаются во внимание следующие температуры:
1) высшая температура – 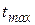 , при которой провод может иметь максимальное удлинение и, следовательно, максимальную стрелу провеса;
, при которой провод может иметь максимальное удлинение и, следовательно, максимальную стрелу провеса;
2) низшая температура – 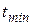 , при которой провод имеет наименьшую длину, а температурные напряжения могут достигать наибольших значений;
, при которой провод имеет наименьшую длину, а температурные напряжения могут достигать наибольших значений;
3) среднегодовая температура 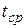 , при которой провод работает наиболее длительное время;
, при которой провод работает наиболее длительное время;
4) температура гололеда - 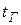 , при наибольшей скорости ветра и при гололеде, как правило, эта температура принимается равной –50С;
, при наибольшей скорости ветра и при гололеде, как правило, эта температура принимается равной –50С;
5) температура грозы - 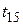 , при которой определяется надежность защиты всех элементов ВЛ тросом в условиях грозового режима, равная +150С.
, при которой определяется надежность защиты всех элементов ВЛ тросом в условиях грозового режима, равная +150С.
3.2 Расчет удельных нагрузок на провода и тросы
Провода и тросы ВЛ испытывают действие нагрузок – вертикальных (вес провода и гололеда) и горизонтальных (давление ветра). В результате этих нагрузок в металле проводов возникают растягивающие напряжения. При расчетах на механическую прочность пользуются удельными нагрузками на провода и тросы. Под удельной нагрузкой понимают равномерно распределенную вдоль провода механическую нагрузку, отнесенную к единице длины и поперечного сечения. Как правило, удельные нагрузки выражаются в даН, отнесенных к 1м длины провода и к 1 мм2 сечения: 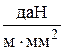 , где 1даН = 10 Н
, где 1даН = 10 Н 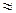 1 кг.
1 кг.
Рассмотрим, как определяются удельные нагрузки.
1. Удельная нагрузка от собственного веса провода (троса) - 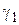 (рис. 3.2).
(рис. 3.2).

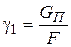 , (3.6)
, (3.6)
где 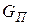 – вес одного метра провода или троса, даН;
– вес одного метра провода или троса, даН;
F – фактическое сечение провода или троса, мм2.
Рис. 3.2.
Значения  для проводов и тросов приводятся в приложениях А и Б.
для проводов и тросов приводятся в приложениях А и Б.
2. Удельная нагрузка от веса гололеда 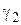 определяется исходя из условия, что гололедные отложения имеют цилиндрическую форму плотностью
определяется исходя из условия, что гололедные отложения имеют цилиндрическую форму плотностью  :
:
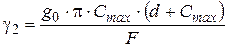 , (3.7)
, (3.7)
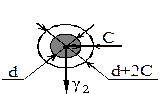 где
где  – толщина стенки гололеда, мм;
– толщина стенки гололеда, мм;
d – диаметр провода или троса, мм;
F – фактическое сечение провода или троса, мм2.
Рис. 3.3
 3. Удельная нагрузка от собственного веса провода (троса) и веса гололеда -
3. Удельная нагрузка от собственного веса провода (троса) и веса гололеда - 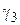 (рис. 3.4):
(рис. 3.4):
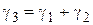 . (3.8)
. (3.8)
Рис. 3.4.
4. Удельная нагрузка от давления ветра, действующего перпендикулярно проводу, при отсутствии гололеда - 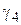 (рис. 3.5):
(рис. 3.5):

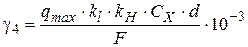 , (3.9)
, (3.9)
Рис. 3.5. где 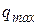 – скоростной напор ветра,
– скоростной напор ветра, 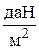 ;
;
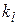 – коэффициент, учитывающий влияние длины пролета на ветровую нагрузку (табл. 3.7);
– коэффициент, учитывающий влияние длины пролета на ветровую нагрузку (табл. 3.7);
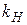 – коэффициент, учитывающий неравномерность скоростного напора ветра по пролету (табл. 3.8);
– коэффициент, учитывающий неравномерность скоростного напора ветра по пролету (табл. 3.8);
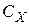 – коэффициент лобового сопротивления, равный 1,1 – для проводов диаметром 20 мм и более, свободных от гололеда; 1,2 – для всех проводов, покрытых гололедом, и для проводов диаметром меньше 20 мм, свободных от гололеда.
– коэффициент лобового сопротивления, равный 1,1 – для проводов диаметром 20 мм и более, свободных от гололеда; 1,2 – для всех проводов, покрытых гололедом, и для проводов диаметром меньше 20 мм, свободных от гололеда.
5. Удельная нагрузка от давления ветра, действующего перпендикулярно проводу, при наличии гололеда - 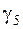 (рис. 3.6):
(рис. 3.6):

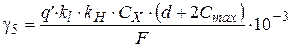 , (3.10)
, (3.10)
где  - для районов с толщиной стенки гололеда до Рис. 3.6 15 мм;
- для районов с толщиной стенки гололеда до Рис. 3.6 15 мм;
 , но не менее 14
, но не менее 14 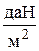 - для районов с толщиной стенки гололеда более 15 мм.
- для районов с толщиной стенки гололеда более 15 мм.
При определении  значение коэффициента
значение коэффициента 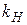 берется из табл. 3.8 для скоростного напора
берется из табл. 3.8 для скоростного напора 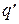 .
.
6. Удельная нагрузка от давления ветра и веса провода (или троса) без гололеда - 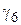 (рис. 3.7):
(рис. 3.7):

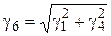 . (3.11)
. (3.11)
Рис. 3.7
7. Удельная нагрузка от давления ветра и веса провода (или троса), покрытого гололедом - 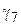 (рис. 3.8):
(рис. 3.8):

 . (3.12)
. (3.12)
Рис. 3.8
Таблица 3.7
| Длина пролета, м | до 50 | 250 и более | ||
Коэффициент 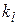
| 1,2 | 1,1 | 1,05 | 1,0 |
Таблица 3.8
| Скоростной напор ветра, даН/м2 | до 27 | 76 и выше | ||
Коэффициент 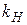
| 1,0 | 0,85 | 0,75 | 0,7 |
3.3 Расчетные климатические условия
При расчетах проводов и тросов ВЛ на механическую прочность необходимо определять напряжения в проводах (тросах) и стрелы провесов при всех возможных эксплуатационных сочетаниях климатических условий. Поскольку таких сочетаний может быть большое количество, то ПУЭ устанавливают следующие расчетные сочетания климатических условий (режимов):
1) высшая температура ( 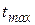 ), ветер и гололед отсутствуют, удельная нагрузка -
), ветер и гололед отсутствуют, удельная нагрузка -  (режим высшей температуры);
(режим высшей температуры);
2) температура минус 50С, ветер отсутствует, провода (тросы) покрыты гололедом, удельная нагрузка - 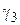 (режим гололеда без ветра);
(режим гололеда без ветра);
3) низшая температура ( 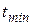 ), ветер и гололед отсутствуют, удельная нагрузка -
), ветер и гололед отсутствуют, удельная нагрузка -  (режим низшей температуры);
(режим низшей температуры);
4) среднегодовая температура ( 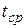 ), ветер и гололед отсутствуют, удельная нагрузка -
), ветер и гололед отсутствуют, удельная нагрузка -  (режим среднегодовой температуры);
(режим среднегодовой температуры);
5) температура минус 50С, максимальный напор ветра, гололед отсутствует, удельная нагрузка - 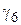 (режим наибольшей нагрузки);
(режим наибольшей нагрузки);
6) температура минус 50С, провода и тросы покрыты гололедом, напор ветра 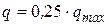 , удельная нагрузка -
, удельная нагрузка - 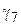 (режим наибольшей нагрузки);
(режим наибольшей нагрузки);
7) температура плюс 150С, ветер и гололед отсутствуют, удельная нагрузка -  (грозовой режим).
(грозовой режим).
В районах со среднегодовой температурой минус 50С и ниже температуры для режимов 5 и 6 следует принимать минус 100С. Режимы 1 и 2 определяют наибольшую вертикальную стрелу провеса, которая может быть при высшей температуре или при гололеде без ветра. В режимах 3,4,5 и 6 выполняется проверка проводов и тросов по допустимому напряжению в условиях низшей и среднегодовой температуры и в условиях наибольшей внешней нагрузки  . При
. При 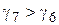 наибольшая внешняя нагрузка будет обусловлена гололедом (режим 6), при
наибольшая внешняя нагрузка будет обусловлена гололедом (режим 6), при 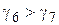 ветром (режим 5). Режим 7 необходим для проверки условий защиты элементов ВЛ тросом во время грозы.
ветром (режим 5). Режим 7 необходим для проверки условий защиты элементов ВЛ тросом во время грозы.
3.4 Уравнение состояния провода (троса)
Расчет проводов и тросов ВЛ на механическую прочность включает в себя определение напряжений при различных условиях работы. При изменении климатических условий меняются удельные нагрузки, температура провода и напряжение в его материале. Для определения напряжений в материале провода при разных климатических условиях используют уравнение состояния провода, которое имеет следующий вид:
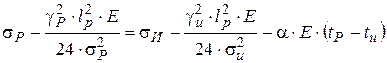 , (3.13)
, (3.13)
где 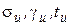 - напряжение в материале провода, удельная нагрузка и температура в исходном режиме;
- напряжение в материале провода, удельная нагрузка и температура в исходном режиме;
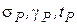 - напряжение в материале провода, удельная нагрузка и температура в рассчитываемом режиме;
- напряжение в материале провода, удельная нагрузка и температура в рассчитываемом режиме;
Е,  - модуль упругости и температурный коэффициент линейного удлинения материала провода;
- модуль упругости и температурный коэффициент линейного удлинения материала провода;
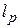 - расчетная длина пролета.
- расчетная длина пролета.
Уравнение состояния связывает указанные выше параметры двух разных режимов. С помощью этого уравнения можно по заданным исходным условиям 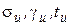 определить напряжение в материале провода
определить напряжение в материале провода 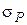 при новых изменившихся условиях
при новых изменившихся условиях 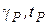 .
.
Относительно неизвестной величины 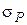 уравнение состояния является неполным кубическим уравнением вида:
уравнение состояния является неполным кубическим уравнением вида:
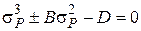 , (3.14)
, (3.14)
где В и D – числовые коэффициенты, полученные в результате подстановки в уравнение состояния всех известных параметров.
3.5 Решение уравнения состояния провода (троса)
Для решения кубического уравнения (3.14) могут быть использованы известные численные и аналитические методы.
Наиболее простым, но требующим больших затрат времени, является метод подбора. Для уменьшения времени расчета необходимо представлять себе приближенное значение искомого напряжения 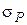 по отношению к исходному напряжению
по отношению к исходному напряжению 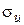 . Например, если в исходном режиме задано напряжение при гололеде
. Например, если в исходном режиме задано напряжение при гололеде 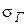 , а требуется найти напряжение при максимальной температуре
, а требуется найти напряжение при максимальной температуре 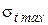 , то искомое напряжение должно быть значительно меньше исходного (в 2-2,5 раза).
, то искомое напряжение должно быть значительно меньше исходного (в 2-2,5 раза).
Примером использования численного метода для решения кубического уравнения может служить метод касательных, который, кроме того, является еще и итерационным. Алгоритм решения этим методом состоит в следующем:
1. Задаемся нулевым приближением - 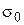 . Выбор нулевого приближения является очень важным моментом расчета, так как в значительной степени определяет число итераций и время расчета. При выборе нулевого приближения следует руководствоваться соображениями, приведенными для метода подбора. В качестве нулевого приближения можно также принять одно из допустимых значений напряжений:
. Выбор нулевого приближения является очень важным моментом расчета, так как в значительной степени определяет число итераций и время расчета. При выборе нулевого приближения следует руководствоваться соображениями, приведенными для метода подбора. В качестве нулевого приближения можно также принять одно из допустимых значений напряжений: 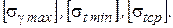 .
.
2. Определяем поправку - 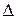 путем деления самой функции на ее первую производную:
путем деления самой функции на ее первую производную:
 ,
,
где i – номер итерации. На первой итерации 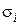 принимается равным
принимается равным 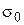 .
.
3. Находим новое значение напряжения 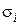 :
:
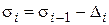 .
.
4. Выполняем проверку окончания итерационного процесса по условию:
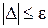 ,
,
где  -заранее заданная точность расчета, которую рекомендуется принимать равной (0,01- 0,03)
-заранее заданная точность расчета, которую рекомендуется принимать равной (0,01- 0,03) 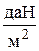 .
.
5. Если условие выполняется, то расчет прекращается, значение 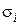 принимается за искомое:
принимается за искомое: 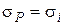 . Если условие не выполняется, то значение
. Если условие не выполняется, то значение 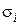 принимается в качестве нового приближения и повторяются расчеты по пунктам 2,3,4.
принимается в качестве нового приближения и повторяются расчеты по пунктам 2,3,4.
3.6 Определение исходного режима
Расчет проводов и тросов ВЛ на механическую прочность ведется методом допустимых напряжений. Суть этого метода заключается в том, что напряжения в проводе или тросе в любом из эксплуатационных режимов не должны превышать допустимых напряжений. При выполнении этого условия материал провода или троса работает в пределах упругих деформаций. Допустимые напряжения задаются ПУЭ [1] в процентах от предела прочности провода или троса для трех режимов:
1) наибольшей нагрузки - 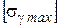 ;
;
2) низшей температуры - 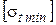 ;
;
3) среднегодовой температуры - 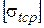 .
.
Значения допустимых напряжений приведены в табл. 3.9.
Таблица 3.9
Допустимые механические напряжения в проводах и тросах
| Провода и тросы | Допустимые напряжения от предела прочности при растяжении, % | Предел прочности, даН/мм2 | |
| при наибольшей нагрузке или низшей температуре | при средне- годовой температуре | ||
| Алюминиевые провода А, АКП | 35-45 | 15-16 | |
| Сталеалюминиевые провода АС, АСКС, АСКП, АСК | 35-45 | 24-33* | |
| Стальные провода ПС | |||
| Тросы ТК |
Как видно из таблицы, допустимые напряжения при наибольшей нагрузке и наименьшей температуре принимаются больше соответствующих напряжений при среднегодовой температуре. Это обусловлено относительной кратковременностью первых двух режимов.
Важным этапом расчета проводов и тросов на механическую прочность является определение исходного (начального) режима. В качестве такого режима можно принять любой режим, для которого известны удельная нагрузка, температура и напряжение. Однако при эксплуатации проводов и тросов напряжения в них не должны превышать соответствующих допустимых напряжений для режимов максимальной нагрузки, низшей и среднегодовой температур. Чтобы выполнить это условие, целесообразно при расчете в качестве исходного выбрать режим, в котором напряжение может достигать допустимого.
Для определения исходного режима используются так называемые критические пролеты. Суть понятия “критический пролет” заключается в следующем. На напряжение в проводе или тросе оказывают влияние нагрузка и температура окружающей среды. Их влияние проявляется в большей или меньшей степени в зависимости от длины пролета. При малых пролетах на напряжение в проводе значительное влияние оказывает температура, при больших пролетах – нагрузка. Граничный пролет, при котором влияние температуры и нагрузки на напряжения в проводе оказывается равноопасным, называется критическим.
Условия ограничения напряжения в проводе или тросе в трех указанных выше режимах определяют три критических пролета.
Первый критический пролет ( 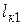 ) – это такой пролет, при котором напряжение в проводе в режиме среднегодовой температуры равно допустимому при среднегодовой температуре, а в режиме низшей температуры – допустимому напряжению при низшей температуре.
) – это такой пролет, при котором напряжение в проводе в режиме среднегодовой температуры равно допустимому при среднегодовой температуре, а в режиме низшей температуры – допустимому напряжению при низшей температуре.
Второй критический пролет ( 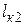 ) – это такой пролет, при котором напряжение в проводе при наибольшей нагрузке равно допустимому напряжению при наибольшей нагрузке, а в режиме низшей температуры – допустимому напряжению при низшей температуре.
) – это такой пролет, при котором напряжение в проводе при наибольшей нагрузке равно допустимому напряжению при наибольшей нагрузке, а в режиме низшей температуры – допустимому напряжению при низшей температуре.
Третий критический пролет ( 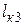 ) – это такой пролет, при котором напряжение в проводе в режиме среднегодовой температуры равно допустимому при среднегодовой температуре, а в режиме наибольшей нагрузки равно допустимому напряжению при наибольшей нагрузке.
) – это такой пролет, при котором напряжение в проводе в режиме среднегодовой температуры равно допустимому при среднегодовой температуре, а в режиме наибольшей нагрузки равно допустимому напряжению при наибольшей нагрузке.
Формулы для определения критических пролетов могут быть получены из уравнения состояния провода. Для вычисления первого критического пролета нужно в правую часть уравнения подставить значения 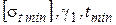 , а в левую -
, а в левую - 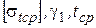 и выразить длину:
и выразить длину:
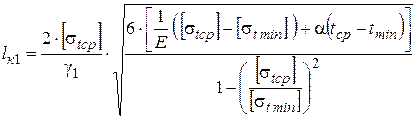 . (3.15)
. (3.15)
Для вычисления второго критического пролета в уравнение состояния провода нужно подставить значения 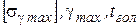 и
и 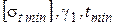 :
:
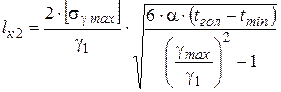 , (3.16)
, (3.16)
где 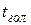 – температура гололеда, равная минус 50С (при
– температура гололеда, равная минус 50С (при 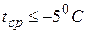
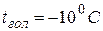 ).
).
Для вычисления третьего критического пролета в уравнение состояния провода нужно подставить 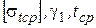 и
и 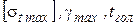 и выразить длину:
и выразить длину:
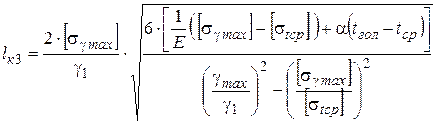 . (3.17)
. (3.17)
В практических расчетах могут иметь место два соотношения между критическими параметрами: 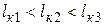 или
или 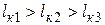 . Кроме того, могут быть случаи, когда
. Кроме того, могут быть случаи, когда 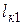 или
или 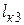 , или оба эти пролета будут мнимыми. Это будет тогда, когда подкоренные выражения в формулах (3.15), (3.17) будут отрицательными.
, или оба эти пролета будут мнимыми. Это будет тогда, когда подкоренные выражения в формулах (3.15), (3.17) будут отрицательными.
Для определения исходного режима по соотношению критических и расчетного пролетов можно воспользоваться табл. 3.10.
Таблица 3.10
Условия выбора исходного режима
Соотношение 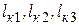
| Соотношение 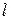 и и 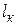
| Параметры исходного режима | ||||
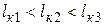
| 
| 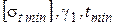
| ||||
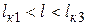
| 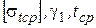
| |||||
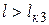
| 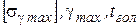
| |||||
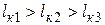
| 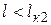
| 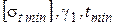
| ||||
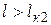
| 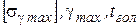
| |||||
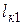 - мнимый - мнимый
| 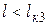
| 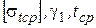
| ||||
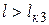
| 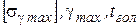
| |||||
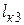 - мнимый - мнимый
| 
| 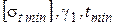
| ||||
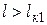
| 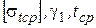
| |||||
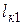 и и 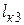 - мнимые - мнимые
| - | 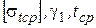
| ||||
3.7 Порядок расчета проводов на механическую прочность
В расчетно-пояснительной записке к курсовому или дипломному проекту рекомендуется выполнять расчет проводов ВЛ на механическую прочность в следующем порядке:
1. Определить удельные нагрузки 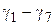 на провода и тросы по формулам 3.6 - 3.12.
на провода и тросы по формулам 3.6 - 3.12.
2. Рассчитать критические пролеты 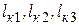 по выражениям (3.15), (3.16), (3.17). По соотношению критических пролетов и расчетного пролета с помощью табл. 3.10 определить исходный режим для расчета провода.
по выражениям (3.15), (3.16), (3.17). По соотношению критических пролетов и расчетного пролета с помощью табл. 3.10 определить исходный режим для расчета провода.
3. По уравнению состояния провода (3.13) рассчитать напряжения в проводе для режимов среднегодовой температуры - 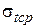 , режима низшей температуры -
, режима низшей температуры -  , наибольшей нагрузки -
, наибольшей нагрузки - 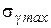 .
.
4. Проверить условия механической прочности проводов:
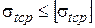 ;
; 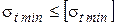 ;
; 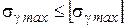 . (3.18)
. (3.18)
Если условия выполняются, то механическая прочность проводов будет достаточной.
5. По уравнению состояния провода (3.13) рассчитать напряжения в проводе для режимов гололеда без ветра - 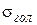 , высшей температуры -
, высшей температуры - 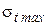 , грозового режима -
, грозового режима - 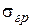 .
.
6. Определить стрелы провеса проводов в режимах, указанных в пункте 5 по формуле:
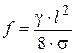 , (3.19)
, (3.19)
где 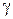 и
и 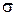 - удельная нагрузка и напряжение в проводе в соответствующем режиме.
- удельная нагрузка и напряжение в проводе в соответствующем режиме.
7. Проверить соблюдение требуемых расстояний от низшей точки провисания провода до земли по условию:
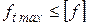 ;
; 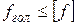 , (3.20)
, (3.20)
где 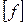 - допустимая стрела провеса провода, определяемая по формуле (3.2).
- допустимая стрела провеса провода, определяемая по формуле (3.2).
Если условия выполняются, то расстояние от нижнего провода до земли будет не менее габаритного размера.
8. Для усвоения методики расчета необходимо выполнить “вручную” вычисления напряжений и стрел провеса в режимах низшей температуры и грозовом режиме. Все остальные расчеты выполняются с помощью ПК по разработанной на кафедре «Электроэнергетические системы» ВятГТУ программе.
3.8 Порядок расчета грозозащитного троса на механическую прочность
Для расчета грозозащитного троса используются методы и приемы расчета проводов. Кроме того, расположение троса на опоре должно быть таким, чтобы гарантировать защиту проводов от ударов молнии. Во избежание перекрытия изоляции между тросом и проводом во время удара молнии должны соблюдаться соответствующие расстояния между тросом и проводами в середине пролета. Напряжения в тросе при наибольшей нагрузке, низшей и среднегодовой температурах не должны превышать соответствующих допустимых напряжений. Защитный угол троса учитывается при разработке конструкций опор (см. п. 2.4).
Наименьшие допустимые расстояния между тросом и проводом в середине пролета (z) без учета отклонения их ветром приведены в табл. 3.1. Допустимые расстояния должны соблюдаться для условий грозового режима, когда на провода и тросы воздействуют нагрузки от собственного веса, ветер отсутствует и температура воздуха равна плюс 150С. Поэтому указанный режим принимается в качестве исходного для механического расчета троса. С учетом этого обстоятельства рекомендуется выполнять расчет троса на механическую прочность в следующем порядке:
1. Определить стрелу провеса троса в грозовом режиме (рис. 3.9) по формуле, м:
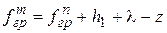 ,
,
где 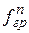 - стрела провеса провода в середине пролета в грозовом режиме, м;
- стрела провеса провода в середине пролета в грозовом режиме, м;
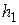 - расстояние по вертикали между верхней траверсой и точкой крепления троса, м;
- расстояние по вертикали между верхней траверсой и точкой крепления троса, м;
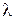 - длина гирлянды изоляторов, м;
- длина гирлянды изоляторов, м;
z – допустимое расстояние между тросом и проводом в середине пролета, м.
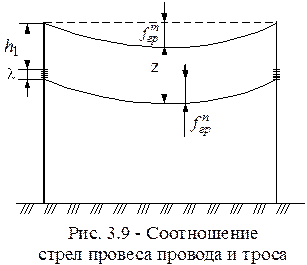 2. Определить напряжение в тросе в грозовом режиме по найденной в п. 1 стреле провеса:
2. Определить напряжение в тросе в грозовом режиме по найденной в п. 1 стреле провеса:
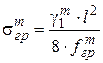 .
.
3. Принять в качестве исходного грозовой режим с известными параметрами: 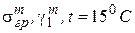 . По уравнению состояния провода (3.13) определить напряжение в тросе для режимов максимальной нагрузки, низшей и среднегодовой температуры (
. По уравнению состояния провода (3.13) определить напряжение в тросе для режимов максимальной нагрузки, низшей и среднегодовой температуры ( 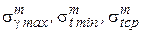 ).
).
4. Проверить условия механической прочности троса:
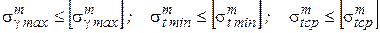 .
.
Если условия выполняются, то можно сделать вывод о пригодности выбранного троса для условий проектируемой линии в нормальных режимах работы. В противном случае необходимо изменить сечение троса, увеличить высоту его подвеса или предусмотреть другие мероприятия.
3.9 Пример расчета провода на механическую прочность
В качестве примера рассмотрим расчет на механическую прочность провода АС-120/19 воздушной ЛЭП напряжением 110 кВ, проходящей во II районе по гололеду (С = 10 мм) и в III районе по ветру (q = 50 даН/м2), в населенной местности с температурами: 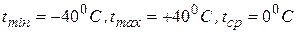 . Линия выполнена с использованием промежуточных опор ПБ110-1. Расчетная длина пролета
. Линия выполнена с использованием промежуточных опор ПБ110-1. Расчетная длина пролета 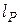 = 240 м.
= 240 м.
Из таблицы А1 приложения А выпишем физико-механические характеристики провода:
1) сечение, мм2: алюминиевой части – 118
стальной части – 18,8
суммарное – 136,8;
2) диаметр провода, мм - 15,2;
3) вес провода, даН/км – 471;
4) модуль упругости, даН/мм2 -  ;
;
5) температурный коэффициент линейного удлинения, 1/град - 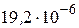 ;
;
6) допустимые напряжения, даН/мм2:
при средней температуре – 8,7
при низшей температуре – 13,0
при наибольшей нагрузке – 13,0.
1. Определим толщину стенки гололеда на проводе и величину скоростного напора ветра.
1.1. Средняя высота подвеса проводов на опоре, м:
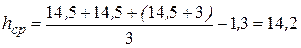 .
.
1.2. Допустимая стрела провеса провода (по формуле 3.2), м:
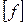 = 14,5 – 1,3 – 6,0 = 7,2.
= 14,5 – 1,3 – 6,0 = 7,2.
1.3. Высота приведенного центра тяжести провода (по формуле 3.1), м:
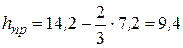 .
.
1.4. Определим толщину стенки гололеда на проводе по формуле (3.5), мм:
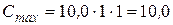 .
.
1.5. Определим скоростной напор ветра на провод по формуле (3.4), даН/м2:
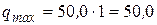 .
.
2. Определим удельные нагрузки на провод.
2.1. Удельную нагрузку от собственного веса провода можно определить по формуле (3.6), 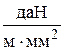 :
:
 .
.
2.2. Удельную нагрузку от веса гололеда определим по формуле (3.7), 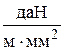 :
:
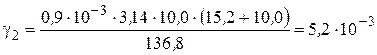 .
.
2.3. Удельную нагрузку от собственного веса провода и веса гололеда определим по формуле (3.8), 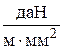 :
:
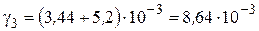 .
.
2.4. Удельную нагрузку от давления ветра при отсутствии гололеда определим по формуле (3.9), 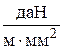 :
:
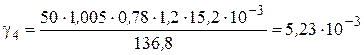 .
.
Коэффициент 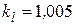 определен линейной интерполяцией по таблице 3.7. Коэффициент
определен линейной интерполяцией по таблице 3.7. Коэффициент 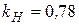 определен по таблице 3.8. Коэффициент
определен по таблице 3.8. Коэффициент 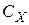 принят равным 1,2.
принят равным 1,2.
2.5. Определим удельную нагрузку от давления ветра на провод при наличии гололеда по формуле (3.10), 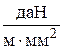 :
:
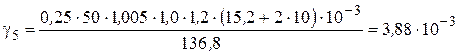 .
.
Коэффициент  определен по табл. 3.8 для
определен по табл. 3.8 для 
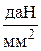 .
.
2.6. Определим удельную нагрузку от давления ветра и веса провода без гололеда по формуле (3.11), 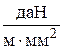 :
:
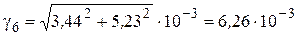 .
.
2.7. Определим удельную нагрузку на провод от давления ветра и веса провода, покрытого гололедом по формуле (3.12), 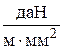 :
:
 .
.
3. Вычислим критические пролеты.
3.1. Первый критический пролет 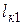 определим по формуле (3.15), м:
определим по формуле (3.15), м:
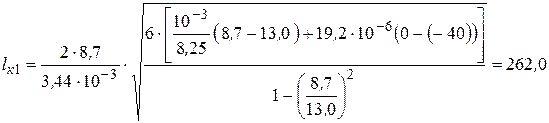 .
.
3.2. Второй критический пролет  определим по формуле (3.16), м:
определим по формуле (3.16), м:
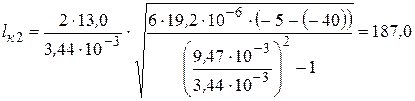 .
.
3.3. Третий критический пролет 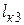 определим по формуле (3.17), м:
определим по формуле (3.17), м:
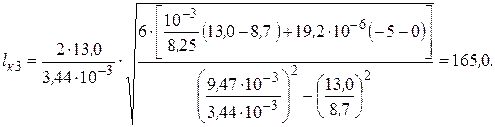
В результате получим следующее соотношение критических пролетов и расчетного пролета: 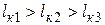 и
и 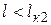 . На основании этих соотношений с помощью табл. 3.10 определим исходный режим. Это режим максимальной нагрузки с параметрами:
. На основании этих соотношений с помощью табл. 3.10 определим исходный режим. Это режим максимальной нагрузки с параметрами: 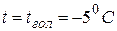 ;
; 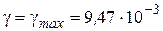
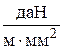 ;
; 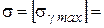
= 13,0 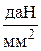 .
.
4. По уравнению состояния провода (3.13) рассчитаем напряжения в проводе для режимов среднегодовой температуры - 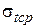 , режима низшей температуры -
, режима низшей температуры -  и наибольшей нагрузки -
и наибольшей нагрузки - 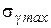 .
.
4.1. Расчет напряжения в проводе для режима низшей температуры выполним “вручную”. Для этого подставим все известные параметры в уравнение (3.13):
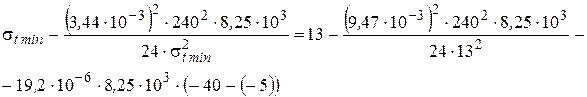 Приведем данное уравнение к виду, соответствующему выражению (3.14):
Приведем данное уравнение к виду, соответствующему выражению (3.14):
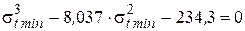 .
.
Решение полученного уравнения выполним итерационным методом касательных. В качестве нулевого приближения примем значение 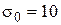
 .
.
4.1.1. Определим поправку на первой итерации:
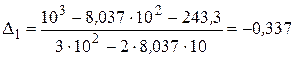 .
.
4.1.2. Найдем новое значение напряжения:
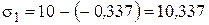
4.1.3. Выполним проверку окончания итерационного процесса. Для этого зададимся точностью расчета 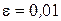
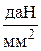 :
:
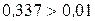 ,
,
следовательно, расчет нужно продолжить, приняв в качестве нового приближения  .
.
4.1.4. Определим поправку на второй итерации:
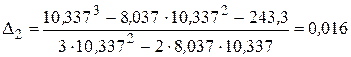 .
.
4.1.5. Найдем новое значение напряжения:
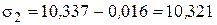 .
.
4.1.6. Выполним проверку:
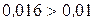 .
.
4.1.7. Определим поправку на третьей итерации:
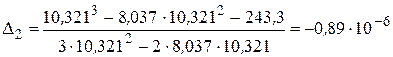 .
.
4.1.8. Выполним проверку:
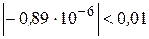 ,
,
следовательно, за искомое значение  принимаем
принимаем 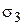 :
:
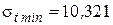
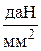 .
.
4.2. Расчеты напряжений в проводе для режимов среднегодовой температуры и наибольшей нагрузки выполним с помощью программы «MERA2». В результате получим:
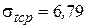
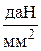 ;
; 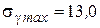
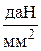 .
.
5. Выполним проверку условий механической прочности проводов по выражениям (3.18):
6,79 < 8,7 10,321 < 13,0 13,0 = 13,0
Условия выполняются – значит, механическая прочность проводов будет достаточной для условий проектируемой линии.
6. По уравнению состояния провода (3.13) выполним расчеты напряжения для режимов гололеда без ветра - 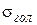 , высшей температуры -
, высшей температуры - 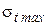 , грозового режима -
, грозового режима - 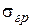 . Результаты расчетов следующие:
. Результаты расчетов следующие:
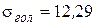
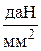 ;
; 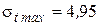
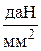 ;
; 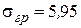
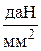 .
.
7. Определим стрелы провеса проводов в режимах гололеда без ветра, высшей температуры и грозового режима по формуле (3.19):
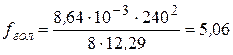 м;
м;
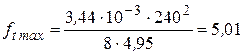 м;
м;
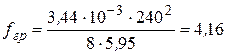 м.
м.
8. Выполним проверку соблюдения требуемых расстояний от низшей точки провисания провода до земли по соотношениям (3.20):
5,01 < 7,2 5,06 < 7.2
Условия выполняются – значит, расстояние от провода до земли будет не менее габаритного размера.
Дата добавления: 2015-02-25; просмотров: 7552;
