История создания СКМ
Первый этап – компьютер, оправдывая свое название (в переводе с англ. "вычислитель"), работал как мощный программируемый калькулятор, способный быстро и автоматически (по веденной программе) выполнять сложные и громоздкие арифметические и логические операции над числами.
Успехи вычислительной математики и постоянно совершенствующиеся численные методы позволяют решить таким способом любую математическую задачу применительно к любой отрасли знаний. Важно отметить, что результат вычислений при этом представляется одним конечным числом в арифметическом виде, то есть при помощи десятичных цифр. Иногда результат представляется множеством (массивом, матрицей) таких чисел, но существо представления от этого не меняется – результат в виде конечного десятичного арифметического числа.
Однако такой результат часто не удовлетворял профессиональных математиков, и вот почему. Подавляющее большинство результатов нетривиальных математических вычислений в классической математике традиционно записывается в символьной форме: с использованием специальных общеизвестных чисел: 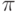 ,
,  ,
,  , а иррациональные значения – с помощью радикала. Считается, что в противном случае имеет место принципиальная потеря точности.
, а иррациональные значения – с помощью радикала. Считается, что в противном случае имеет место принципиальная потеря точности.
Другой классический пример, вызывающий замечание математика – выражение, знакомое любому школьнику:
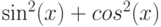
всегда равное единице; а в компьютере либо будет предпринята попытка вычислить это выражение (с неизбежными ошибками округления), либо будет выдано сообщение о неопределенности аргумента Х и всякие дальнейшие действия будут прекращены.
На этом первый этап завершился...
Естественно, вслед за стремительным совершенствованием компьютерных систем человеку в компьютерных расчетах захотелось большего: почему бы не заставить компьютер выполнять преобразования традиционными для математики способами (дробно-рациональные преобразования, подстановки, упрощения, решение уравнений, дифференцирование и т.п.).
Их принято называть преобразованиями в символьном виде или аналитическими преобразованиями, а результат получать не как раньше – в виде одного числа, а в виде формулы.
К этому моменту практически все области человеческой деятельности оказались охваченными каждая своим собственным математическим аппаратом и обзавелись собственными пакетами прикладного программного обеспечения (ППО). При этом всем понадобился универсальный математический инструмент, ориентированный на широкий круг пользователей, которые не являются ни профессионалами в математике, ни программистами, воспитанными на узкоспециальных, малопонятных большинству конечных пользователей компьютерных языках.
Это привело к созданию компьютерных систем символьной математики, рассчитанных на широкие круги пользователей – непрофессионалов в математике. Так началась с середины 60-х годов ХХ века эра систем компьютерной математики (СКМ), по-английски CAS – Сomputer algebra system.
В конце 60-х годов в России на отечественных ЭВМ серии "Мир", разработанных под руководством академика В. Глушкова, была реализована СКМ на языке программирования "Аналитик", обладающая всеми возможностями символьных вычислений, впрочем, с весьма скромными, по нынешним понятиям, характеристиками.
Конечно, даже самые простые неинтеллектуальные компьютерные математические справочники представляют большой практический интерес – ведь ни один самый способный человек не в состоянии вместить в своей голове все математические законы и правила, созданные за многовековую историю человечества.
Данные об особенностях существующих СКМ приведены в табл. 12.1.
| Таблица 12.1. Современные СКМ и их возможности | ||
| Система | Назначение и возможности | Недостатки |
| Mathcad 13, Mathcad 14 | Система универсального назначения в основном для непрофессиональных математиков и целей образования всех ступеней. Продуманный интерфейс представления данных в традиционной математической форме и изумительная графика на всех этапах работы, включая ввод. Ввод с помощью выбора из панелей инструментов или из меню практически без использования клавиатуры. Мощный и исчерпывающий набор операторов и функций. Множество примеров, электронных книг и библиотек, готовых решений практических задач. Ядро символьных вычислений импортировано из СКМ Maple. Предоставление серверных услуг профессионального пакета. Легкость переноса документа в другие приложения | Достаточно примитивные средства программирования. Дороговизна электронных книг и библиотек, отсутствие русифицированных версий самого пакета и дополнительных библиотек (книг). Затруднена символьная обработка дифференциальных уравнений. Не создается итоговый исполняемый *.exe-файл; для запуска документа необходимо наличие пакета СКМ Mathcad. Затруднения при выполнении тригонометрических преобразований |
| Maple V R4/R5/R6 | Университетское высшее образование и научные расчеты. Мощное ядро символьных вычислений – возможности аналогичны СКМ Mathcad, содержащее до 3000 функций. Мощнейшая графика. Удобная справочная система. Средства форматирования документов | Повышенные требования к аппаратным ресурсам. Отсутствие синтеза звуков. Ориентация на опытных пользователей и специалистов по математике. Все недостатки аналитических действий аналогичны СКМ Mathcad |
| Mathematica 5/7 | Высшее образование и научные расчеты. Наиболее развитая система символьной математики. Единственная СКМ, обеспечивающая символьное решение дифференциальных уравнений. Совместимость с разными компьютерными платформами. Уникальная трехмерная графика. Поддержка синтеза звука. Развитые средства форматирования документов. Программный синтез звуков. | Высокие требования к аппаратным ресурсам. Чрезмерная защита от копирования. Слабая защита от некорректных задач. Ориентация на опытных пользователей. Ввод задач на уникальном языке функционального программирования. Непривычная индикация функций запуска вычислений. |
| MATLAB 7.* | Образование (в том числе техническое), научные расчеты, численное моделирование, и расчеты, ориентированные на применение матричных методов, при этом скаляр рассматривается как матрица 1х1. Уникальные матричные средства, обилие численных методов, описательная (дескрипторная) графика, высокая скорость вычислений, легкость адаптации к задачам пользователя благодаря множеству пакетов расширения системы. Развитый язык программирования с возможностями объектно-ориентированного программирования (ООП), совместимость с алгоритмическим языком Java | Очень высокие требования к аппаратным ресурсам. Практически отсутствует возможность символьных вычислений. Относительно высокая стоимость. Ввод задач на уникальном языке программирования |
Рассмотрим внутреннюю архитектуру СКМ на примере наиболее мощной, по мнению ряда авторитетных специалистов [6], СКМ Mathematica, обладающей наиболее развитой системой символьной математики. На рис.12.1 представлена ее программная архитектура.
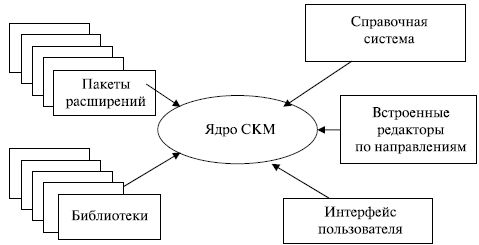
Рис. 12.1.Архитектура обобщенной СКМ
Центральная часть – ядро (Kernel) системы СКМ реализует алгоритм функционирования СКМ, обеспечивает совместное функционирование всех ее частей, организует прием и интеллектуальную обработку запроса пользователя, а затем – вызов нужной процедуры решения. В ядре помещается большое количество встроенных функций и операторов системы. Их количество в современных СКМ может достигать многих тысяч. Например, ядро системы Mathematica 4 содержит данные более чем 5000 одних только интегралов, хотя для интегрирования используются только несколько встроенных функций.
Поиск и выполнение функций и процедур, встроенных в ядро СКМ, выполняется быстро, если их там не слишком много. Поэтому объем ядра ограничивают, но к нему добавляют встроенные в СКМ библиотеки процедур и функций, использующихся относительно редко. При этом общее число доступных пользователю математических функций ядра и этих встроенных библиотек достигает многих тысяч.
Кардинальное расширение возможностей СКМ и их приспособленность к нуждам конкретных пользователей для углубленного решения определенного круга задач (например, задач теоретической и прикладной статистики, векторного анализа) достигается за счет установки внешних пакетов расширения. Эти пакеты, приобретаемые отдельно, делают возможности СКМ практически безграничными.
Все эти библиотеки, пакеты расширений и справочная система современных СКМ (назовем их инструментами СКМ) содержат не только и не просто знания в области математики, накопленные за много веков ее развития (этим никого не удивишь: именно такие возможности характерны для широко распространенного класса ИПО – информационно-поисковых систем). Но восхищает, что эти инструменты удивительным образом автоматически и творчески используют такие знания для решения задач, где нужно выбрать и уметь применить один, единственный из многих десятков, неочевидный метод решения. Например, СКМ могут мгновенно найти неопределенный интеграл либо сразу же сообщить о невозможности его представления элементарными функциями – задача непростая, даже для профессионального математика. Не менее впечатляет и то, что если после получения искомой формулы перейти к началу документа и задать входящим в эту формулу параметрам конкретные числовые значения, мгновенно будет получен ее численный результат. В состав любой СКМ входит набор редакторов (на рис.12.1 они названы редакторами по направлениям): текстовый, формульный, графический редакторы, средства поддержки работы в сети и HTML(XML)-средства, пакеты анимации и аудиосредства.
Благодаря всем этим возможностям СКМ могут быть отнесены к программным продуктам самого высокого на сегодняшний день уровня – интеллектуального. Такие программы в настоящее время объединяются термином "базы знаний". Современные СКМ, по мнению признанных авторитетов [6, 7], предоставляет неискушенному пользователю возможности выпускника математического вуза в областях численных методов расчета, математического анализа, теории матриц и других общих разделах высшей математики, позволяющих получить конструктивные результаты.
Конечно, в абстрактных разделах математики, типа функционального анализа или вопросов "существования и единственности..." СКМ пока вряд ли могут быть полезны (кроме как для предоставления нужной справки, что очень даже немало), но в прикладных задачах, для которых СКМ и создавались, такие разделы математики обычно не задействованы.
Дата добавления: 2015-02-25; просмотров: 1141;
