Приборы и материалы.
| № п\п | Наименование прибора | Класс точности
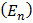
| Цена деления | Предел измерения
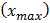
| Точность отсчета
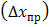
|
| Термостат | – | – | – | – | |
| Термопара | – | – | – | – | |
| Микроамперметр | – | ||||
| Термометр | – |
Теоретические сведения
Основные понятия и законы
1.1. Электронная эмиссия. Работа выхода электрона из металла
Рассмотрим процесс с точки зрения классической электронной теории.
В узлах кристаллической решетки находятся положительные ионы, а между ними свободно движутся электроны. Они как бы плавают по всему объему проводника, так как силы притяжения к положительным ионам решетки, действующие на свободные электроны, находящиеся внутри металла, в среднем взаимно уравновешиваются. Действие сил притяжения со стороны положительных ионов на электроны мешает последним выйти за пределы поверхности металла. Лишь наиболее быстрые электроны могут преодолеть это притяжение и вылететь из металла. Однако совсем покинуть металл электрон не может, так как притягивается положительным поверхностным ионом и тем зарядом, который возник в металле в связи с потерей электрона. Равнодействующая этих сил притяжения не равна нулю, а направлена внутрь металла перпендикулярно его поверхности (рис. 1).
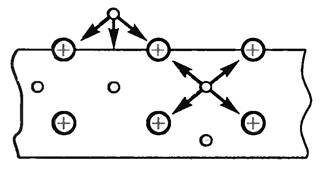 Рис. 1.
Рис. 1.
|
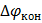 в этом слое называется контактной разностью потенциалов между металлом и вакуумом.
в этом слое называется контактной разностью потенциалов между металлом и вакуумом.
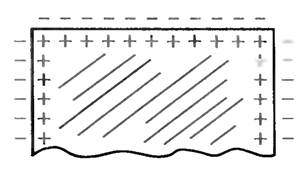 Рис. 2.
Рис. 2.
|
Как показывают расчеты и специально поставленные опыты, толщина этого слоя мала и равна примерно 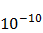 м.
м.
Таким образом, чтобы покинуть металл и уйти в окружающую среду, электрон должен совершить работу 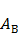 против сил притяжения со стороны положительного заряда металла и против сил отталкивания от отрицательно заряженного электронного облака. Она приблизительно равна:
против сил притяжения со стороны положительного заряда металла и против сил отталкивания от отрицательно заряженного электронного облака. Она приблизительно равна:
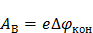 ,
,
где  – заряд электрона. Для этого электрон должен обладать достаточной кинетической энергией.
– заряд электрона. Для этого электрон должен обладать достаточной кинетической энергией.
Минимальную работу 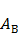 , которую должен совершить электрон за счет своей кинетической энергии для того, чтобы выйти из металла в вакуум и не вернуться в него, называют работой выхода.
, которую должен совершить электрон за счет своей кинетической энергии для того, чтобы выйти из металла в вакуум и не вернуться в него, называют работой выхода.
Единицами измерения работы выхода являются: в СИ – Джоуль (Дж) или внесистемная единица – электронвольт (эВ)[2]. Для чистых металлов 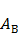 составляет несколько электронвольт. Так, например, для цезия ее значение равно 1,81 эВ, для платины 6,27 эВ.
составляет несколько электронвольт. Так, например, для цезия ее значение равно 1,81 эВ, для платины 6,27 эВ.
Таким образом, можно назвать две вероятные причины появления работы выхода:
1. Если электрон по какой-то причине удаляется из металла, то в том месте, которое электрон покинул, возникает избыточный положительный заряд и электрон притягивается к индуцированному им самим положительному заряду.
2. Отдельные электроны, покидая металл, удаляются от него на расстояния порядка атомных и создают, тем самым, над поверхностью металла «электронное облако», плотность которого быстро убывает с расстоянием. Это облако вместе с наружным слоем положительных ионов решетки образует двойной электрический слой, поле которого подобно полю плоского конденсатора. Толщина этого слоя равна нескольким межатомным расстояниям 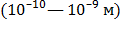 . Он не создает электрического поля во внешнем пространстве, но препятствует выходу свободных электронов из металла.
. Он не создает электрического поля во внешнем пространстве, но препятствует выходу свободных электронов из металла.
Работа выхода производится электронами – за счет уменьшения их кинетической энергии. Поэтому понятно, что медленно движущиеся электроны вырваться из металла не могут Электрон проводимости может вылететь из какого либо металла в том случае, если его энергия 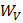 превышает работу выхода
превышает работу выхода 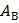 электрона из металла.
электрона из металла.
Выход свободных электронов из металла называется эмиссией электронов. При нормальных внешних условиях электронная эмиссия выражена слабо, так как средняя кинетическая энергия хаотического теплового движения большинства свободных электронов в металлах гораздо меньше работы выхода. Для повышения интенсивности эмиссии следует увеличить кинетическую энергию свободных электронов до значений, равных или больших значения работы выхода. Этого можно достигнуть различными способами. Во-первых, созданием электрического поля очень большой напряженности 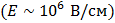 , способного вырвать электроны из металла, – холодная эмиссия. Такая эмиссия используется в электронных микропроекторах. Во-вторых, бомбардировкой металла электронами, предварительно разогнанными электрическим полем до очень большой скорости, – вторичная электронная эмиссия. В-третьих, интенсивным освещением поверхности металла – фотоэмиссия. На явлении фотоэмиссии основан внешний фотоэффект и устройство вакуумного фотоэлемента. В-четвертых, нагревание металла – термоэлектронная эмиссия. Электроны, испускаемые нагретым телом, называются термоэлектронами, а само это тело – эмиттером.
, способного вырвать электроны из металла, – холодная эмиссия. Такая эмиссия используется в электронных микропроекторах. Во-вторых, бомбардировкой металла электронами, предварительно разогнанными электрическим полем до очень большой скорости, – вторичная электронная эмиссия. В-третьих, интенсивным освещением поверхности металла – фотоэмиссия. На явлении фотоэмиссии основан внешний фотоэффект и устройство вакуумного фотоэлемента. В-четвертых, нагревание металла – термоэлектронная эмиссия. Электроны, испускаемые нагретым телом, называются термоэлектронами, а само это тело – эмиттером.
ром.
1.2. Понятие о «потенциальной яме»
Потенциа́льная я́ма – ограниченная область пространства, определяемая физической природой взаимодействия частиц, в которой потенциальная энергия частицы меньше, чем вне её.
Термин «потенциальная яма» (П.я.) происходит от вида графика, изображающего зависимость потенциальной энергии 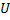 частицы в силовом поле от её положения в пространстве (в случае одномерного движения – от координаты
частицы в силовом поле от её положения в пространстве (в случае одномерного движения – от координаты  ; рис. 3). Такая форма зависимости
; рис. 3). Такая форма зависимости  возникает в поле сил притяжения, т.е. потенциальная яма обычно отвечает силам притяжения.
возникает в поле сил притяжения, т.е. потенциальная яма обычно отвечает силам притяжения.
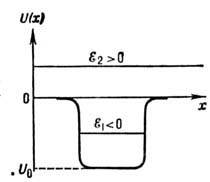 Рис. 3. Схематическое изображение потенциальной ямы
Рис. 3. Схематическое изображение потенциальной ямы  (
( 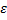 – полная энергия частицы). – полная энергия частицы).
|
Характеристиками потенциальной ямы являются её ширина
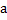 (расстояние, на котором проявляется действие сил притяжения) и глубина
(расстояние, на котором проявляется действие сил притяжения) и глубина 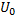 , равная разности между значением потенциальной энергии на бесконечно большом расстоянии (обычно принимаемым за нуль) и её минимальным значением внутри ямы (рис. 3).
, равная разности между значением потенциальной энергии на бесконечно большом расстоянии (обычно принимаемым за нуль) и её минимальным значением внутри ямы (рис. 3).
Примером потенциальной ямы может служить потенциал притяжения между протоном и нейтроном, экспоненциально убывающий с увеличением расстояния между ними.
В классической механике частица с энергией 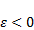 не сможет вылететь из потенциальной ямы. И будет всё время двигаться в ограниченной области пространства внутри ямы (между двумя классическими точками остановки
не сможет вылететь из потенциальной ямы. И будет всё время двигаться в ограниченной области пространства внутри ямы (между двумя классическими точками остановки 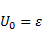 ).
).
Положение частицы на «дне» ямы отвечает устойчивому равновесию и соответствует нулевой кинетической энергии частицы. Если 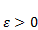 , то частица преодолевает действие сил притяжения и свободно покидает яму.
, то частица преодолевает действие сил притяжения и свободно покидает яму.
Если в потенциальную яму попала частица, энергия которой ниже, чем необходимая для преодоления краёв ямы, то возникнут колебания частицы в яме. Амплитуда колебаний будет обусловлена собственной энергией частицы. Частица, находящаяся на дне потенциальной ямы, пребывает в состоянии устойчивого равновесия, то есть при отклонении частицы от точки минимума потенциальной энергии возникает сила, направленная в противоположную отклонению сторону. Если частица подчиняется квантовым законам, то, несмотря на недостаток энергии, она с определённой вероятностью может покинуть потенциальную яму (явление туннельного эффекта).
Электрон в металле можно рассматривать как частицу, находящуюся в потенциальной яме. При этом с классической точки зрения глубина потенциальной ямы – 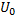 численно равна работе выхода –
численно равна работе выхода – 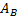 электрона из металла. В квантовом случае работа выхода
электрона из металла. В квантовом случае работа выхода 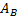 электрона отсчитывается не от «дна» потенциальной ямы, а от так называемого «уровня Ферми» – наивысшего энергетического уровня, занятого электронами в потенциальной яме, в соответствии с принципом Паули[3] (например, от энергетического уровня
электрона отсчитывается не от «дна» потенциальной ямы, а от так называемого «уровня Ферми» – наивысшего энергетического уровня, занятого электронами в потенциальной яме, в соответствии с принципом Паули[3] (например, от энергетического уровня 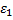 ).
).
1.3. Контактные явления
Если привести два разных металла в соприкосновение, между ними возникает разность потенциалов, которая называется контактной разностью потенциалов (к.р.п.). В результате в окружающем металлы пространстве появляется электрическое поле.
Так как проводники находятся при одинаковой температуре, то в отсутствие приложенного напряжения поле может существовать только в пограничных слоях (правило Вольта).
Контактная разность потенциалов – это разность потенциалов между проводниками, возникающая при соприкосновении двух различных проводников, имеющих одинаковую температуру.
Наиболее важно понятие к. р. п. для твёрдых проводников (металлов и полупроводников). Различают внутреннюю разность потенциалов (при соприкосновении металлов) и внешнюю (в зазоре).
Электрическое поле к. р. п. сосредоточено в проводниках вблизи границы раздела и в зазоре между проводниками. Линейные размеры этой области в металлах имеет атомные размеры 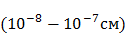 , а в полупроводниках колеблется в широких пределах и может достигать величины
, а в полупроводниках колеблется в широких пределах и может достигать величины 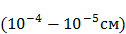 . Отсюда следуют два вывода: 1) из двух соприкасающихся тел к. р. п. приходится в основном на проводники с большим сопротивлением; 2) для полупроводников в области сосредоточения к. р. п. заметно изменяется концентрация носителей заряда.
. Отсюда следуют два вывода: 1) из двух соприкасающихся тел к. р. п. приходится в основном на проводники с большим сопротивлением; 2) для полупроводников в области сосредоточения к. р. п. заметно изменяется концентрация носителей заряда.
1.4. Контактная разность потенциалов с точки зрения классической электронной теории
Появление к.р.п. обусловлено двумя причинами:
1). Различие в работах выхода 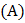 электронов из металлов, приведённых в соприкосновение. В этом случае силы, действующие на электроны в пограничной области со стороны ионных каркасов металлов, не уравновешены и поэтому вызывают переход электронов из одного металла в другой. Разность потенциалов, обусловленная различием работ выхода контактирующих металлов, называется внешней контактной разностью потенциалов.
электронов из металлов, приведённых в соприкосновение. В этом случае силы, действующие на электроны в пограничной области со стороны ионных каркасов металлов, не уравновешены и поэтому вызывают переход электронов из одного металла в другой. Разность потенциалов, обусловленная различием работ выхода контактирующих металлов, называется внешней контактной разностью потенциалов.
2). Различием в плотностях 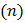 электронного газа в металлах, вследствие чего возникает диффузионный переход электронов из металла, где плотность этого газа больше, в металл, где эта плотность меньше. Разность потенциалов, обусловленная различием в плотностях электронного газа в контактирующих металлах, называется внутренней контактной разностью потенциалов.
электронного газа в металлах, вследствие чего возникает диффузионный переход электронов из металла, где плотность этого газа больше, в металл, где эта плотность меньше. Разность потенциалов, обусловленная различием в плотностях электронного газа в контактирующих металлах, называется внутренней контактной разностью потенциалов.
Рассмотрим действие каждой из этих причин в отдельности.
а) Различие в работах выхода контактирующих металлов
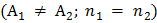 .
.
Если два твёрдых проводника привести в соприкосновение (например, 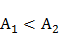 ), то между ними происходит обмен электронами, причём вначале преимущественно электроны переходят из проводника с меньшей работой выхода в проводник с большей работой выхода. В результате этого процесса проводники приобретают электрические заряды противоположных знаков, что приводит к появлению электрического поля, препятствующего дальнейшему перетеканию электронов. В конечном итоге достигается динамическое равновесие, при котором потоки электронов в обоих направлениях становятся одинаковыми, и между проводниками устанавливается к. р. п.
), то между ними происходит обмен электронами, причём вначале преимущественно электроны переходят из проводника с меньшей работой выхода в проводник с большей работой выхода. В результате этого процесса проводники приобретают электрические заряды противоположных знаков, что приводит к появлению электрического поля, препятствующего дальнейшему перетеканию электронов. В конечном итоге достигается динамическое равновесие, при котором потоки электронов в обоих направлениях становятся одинаковыми, и между проводниками устанавливается к. р. п.
Действительно, в этом состоянии на электроны в пограничном слое не должны действовать односторонне направленные силы, т.е. должно выполняться соотношение: 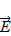 =
= 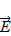 1 +
1 + 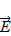 2, или в скалярной форме:
2, или в скалярной форме:
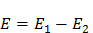 , (1),
, (1),
где 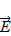 1 и
1 и 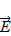 2 – вектора напряжённостей электрических полей, действующих на электрон в пограничной области,
2 – вектора напряжённостей электрических полей, действующих на электрон в пограничной области, 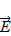 – вектор напряжённости результирующего электрического поля.
– вектор напряжённости результирующего электрического поля.
Умножим формулу (1) на элементарное перемещение 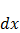 и проинтегрируем вдоль какого-либо пути перехода от одного металла к другому:
и проинтегрируем вдоль какого-либо пути перехода от одного металла к другому:
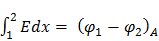 (2)
(2)
–контактная разность потенциалов, обусловленная разностью работ выхода.
Так как, 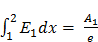 и
и 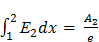 , (3),
, (3),
где  – заряд электрона, то из формул (2) и (3) следует:
– заряд электрона, то из формул (2) и (3) следует:
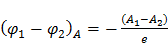 (4),
(4),
где знак «  » учитывает направление вектора напряжённости
» учитывает направление вектора напряжённости 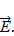
Таким образом, из формулы (4) следует: значение внешней контактной разности потенциалов равно разности работ выхода отнесенной к заряду электрона.
б) Различия в плотностях электронного газа в металлах
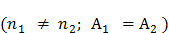
В этом случае 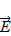 1 =
1 = 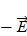 2, т.е. электрические поля, созданные поверхностными слоями металлов в пограничной области взаимно уравновешиваются, поэтому электроны могут свободно переходить из одного металла в другой. При
2, т.е. электрические поля, созданные поверхностными слоями металлов в пограничной области взаимно уравновешиваются, поэтому электроны могут свободно переходить из одного металла в другой. При 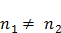 каждый из металлов будет ежесекундно посылать в пограничную область различные количества электронов:
каждый из металлов будет ежесекундно посылать в пограничную область различные количества электронов: 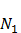 и
и 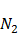 . Из
. Из 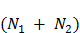 электронов, ежесекундно поступающих в эту область, половина будет втянута в один металл, а другая половина - во второй металл. Таким образом, из первого металла ежесекундно выходят
электронов, ежесекундно поступающих в эту область, половина будет втянута в один металл, а другая половина - во второй металл. Таким образом, из первого металла ежесекундно выходят 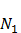 электронов, а поступают
электронов, а поступают 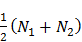 электронов. Разница между этими числами вызовет избыток или недостаток электронов в металле, т.е. положительную или отрицательную зарядку его.
электронов. Разница между этими числами вызовет избыток или недостаток электронов в металле, т.е. положительную или отрицательную зарядку его.
Второй металл приобретёт противоположный заряд. Вследствие этого появится электрическое поле ∆ 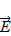 , направленное от положительно заряженного металла к отрицательному, которое приостановит диффузию электронов из одного металла в другой.
, направленное от положительно заряженного металла к отрицательному, которое приостановит диффузию электронов из одного металла в другой.
Таким образом, при 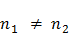 возникает контактное электрическое поле ∆
возникает контактное электрическое поле ∆  , препятствующее выравниванию электронного газа в металлах.
, препятствующее выравниванию электронного газа в металлах.
Внутри этой области плотность электронного газа должна изменяться от 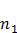 в одном металле до
в одном металле до 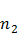 – в другом металле. По аналогии с изменением плотности газа в поле тяготения Земли (барометрическая формула), запишем:
– в другом металле. По аналогии с изменением плотности газа в поле тяготения Земли (барометрическая формула), запишем:
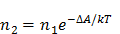 ,
,
где 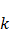 – постоянная Больцмана;
– постоянная Больцмана;  – абсолютная температура;
– абсолютная температура; 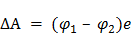 – работа переноса электрона через пограничную область;
– работа переноса электрона через пограничную область; 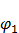 и
и 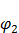 – потенциалы металлов после наступления равновесного состояния.
– потенциалы металлов после наступления равновесного состояния.
Тогда:
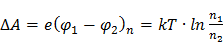 или
или 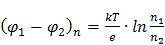 (5)
(5)
Формулы (5) определяет значение внутренней контактной разности потенциалов.
в) Существуют обе причины, вызывающие возникновение контактной разницы потенциалов
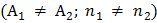
В этом случае с учётом формул (4) и (5) к.р.п. выражается соотношением:
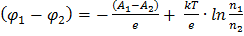 . (6)
. (6)
Из соотношения (6) следует: контактная разность потенциалов зависит только от температуры и химической природы контактирующих металлов.
Электрическое поле 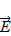 , которое создаётся между металлами вследствие скопления в них избыточных зарядов, будет складываться с внутренними электрическими полями
, которое создаётся между металлами вследствие скопления в них избыточных зарядов, будет складываться с внутренними электрическими полями 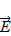 1 и
1 и 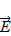 2, которые существуют в поверхностном слое каждого металла. Однако в равновесном состоянии должно выполняться условие:
2, которые существуют в поверхностном слое каждого металла. Однако в равновесном состоянии должно выполняться условие:
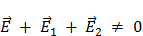 ,
,
т.к. если было бы наоборот, то был бы возможен переход электронов из металла, где плотность электронного газа велика, в металл, де эта плотность мала.
Равновесие может наступить при условии:
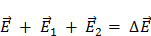 ,
,
где ∆ 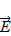 должно быть достаточным для приостановки диффузии электронов.
должно быть достаточным для приостановки диффузии электронов.
Таким образом, в пограничном слое между металлами при равновесии существует только контактное электрическое поле 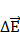 (обусловленное вторым членом формулы (6)).
(обусловленное вторым членом формулы (6)).
г) Контактная разность потенциалов на границе с полупроводником
Мы рассмотрели контакт двух металлов. Однако контактная разность потенциалов возникает и на границе между металлом и полупроводником, а также на границе между двумя полупроводниками.
В случае контакта металла с полупроводником к. р. п. сосредоточена практически в полупроводнике и при достаточно большой величине заметно изменяет концентрацию носителей тока в приконтактной области полупроводника, а, следовательно, и сопротивление этого слоя. Если образуется слой с высоким сопротивлением (обеднённый носителями тока), то при наложении внешней разности потенциалов концентрация носителей заряда будет в нём заметно меняться, причём несимметричным образом в зависимости от знака внешнего напряжения. Т.о., к.р.п. обусловливает нелинейность вольтамперных характеристик контактов металл – полупроводник, которые благодаря этому обладают выпрямительными свойствами.
В случае контакта двух полупроводников из одного вещества, но с различными типами проводимости к. р. п. приводит к образованию переходного слоя объёмного заряда с нелинейной зависимостью сопротивления от внешнего напряжения.
К. р. п. играет важную роль в физике твёрдого тела и её приложениях. Она оказывает заметное влияние на работу электровакуумных приборов. В электронных лампах к. р. п. между электродами складывается с приложенными внешними напряжениями и влияет на вид вольтамперных характеристик. В термоэлектронном преобразователе энергии к. р. п. используется для прямого преобразования тепловой энергии в электрическую. Электроны "испаряются" из горячего катода с большой работой выхода и "конденсируются" на аноде с малой работой выхода. Разность в потенциальной энергии электронов превращается в работу, производимую во внешней электрической цепи.
1.5. Контактная разность потенциалов с точки зрения зонной (квантовой) теории твёрдого тела
Для объяснения внутренней контактной разности потенциалов прибегают к модели свободных электронов в металлах. Допустим, что температура металла равна 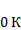 . Тогда все энергерические уровни вплоть до уровня Ферми будут заполнены электронами. Так как энергии Ферми разные для разных металлов, то разными будут и концентрации электронов проводимости. Таким образом, для приведенных в соприкосновение металлов начнётся диффузия электронов. То есть, металл с большим уровнем Ферми будет заряжаться положительно, а второй металл приобретёт отрицательный заряд. На границе возникнет скачок потенциала, или, что, то же самое – электрическое поле, препятствующее дальнейшей диффузии электронов. При определенной разности потенциалов диффузия прекратится, это произойдет, когда уровни Ферми обоих металлов сравняются (рис. 4). Это явление наблюдается и при ненулевой температуре. Внутренняя разность потенциалов равна разности уровней Ферми, отнесенных к заряду электрона (7). Что касается внешней разности потенциалов то ход рассуждений остается прежний. В зазоре между металлами возникает электрическое поле, а сами поверхности заряжены.
. Тогда все энергерические уровни вплоть до уровня Ферми будут заполнены электронами. Так как энергии Ферми разные для разных металлов, то разными будут и концентрации электронов проводимости. Таким образом, для приведенных в соприкосновение металлов начнётся диффузия электронов. То есть, металл с большим уровнем Ферми будет заряжаться положительно, а второй металл приобретёт отрицательный заряд. На границе возникнет скачок потенциала, или, что, то же самое – электрическое поле, препятствующее дальнейшей диффузии электронов. При определенной разности потенциалов диффузия прекратится, это произойдет, когда уровни Ферми обоих металлов сравняются (рис. 4). Это явление наблюдается и при ненулевой температуре. Внутренняя разность потенциалов равна разности уровней Ферми, отнесенных к заряду электрона (7). Что касается внешней разности потенциалов то ход рассуждений остается прежний. В зазоре между металлами возникает электрическое поле, а сами поверхности заряжены.
Различная зависимость от температуры контактной разности потенциалов 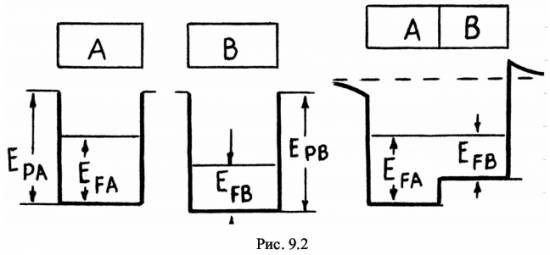 Рис. 4.
Рис. 4.
Контактная разность потенциалов вызвана отличием энергий Ферми у контактирующих различных проводников. При создании контакта химические потенциалы электронов становятся одинаковыми, и возникает контактная разность потенциалов, равная:
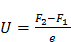 , (7)
, (7)
где 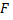 – энергия Ферми,
– энергия Ферми, 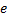 – заряд электрона.
– заряд электрона.
На контакте тем самым существует электрическое поле, локализованное в тонком приконтактном слое. Если составить замкнутую цепь из двух металлов, то 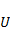 возникает на обоих контактах. Электрическое поле будет направлено одинаковым образом в обоих контактах – от большего вектора напряженности электрического поля
возникает на обоих контактах. Электрическое поле будет направлено одинаковым образом в обоих контактах – от большего вектора напряженности электрического поля 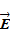 к меньшему. Это значит, что если совершить обход по замкнутому контуру, то в одном контакте обход будет происходить по полю, а в другом – против поля. Циркуляция вектора
к меньшему. Это значит, что если совершить обход по замкнутому контуру, то в одном контакте обход будет происходить по полю, а в другом – против поля. Циркуляция вектора 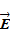 тем самым будет равна нулю.
тем самым будет равна нулю.
Если температура одного из контактов изменится на 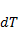 , то, поскольку энергия Ферми зависит от температуры,
, то, поскольку энергия Ферми зависит от температуры, 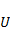 также изменится. Но если изменилась внутренняя контактная разность потенциалов, то изменилось электрическое поле в одном из контактов, и поэтому циркуляция вектора
также изменится. Но если изменилась внутренняя контактная разность потенциалов, то изменилось электрическое поле в одном из контактов, и поэтому циркуляция вектора 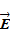 будет отлична от нуля, то есть появляется ЭДС в замкнутой цепи.
будет отлична от нуля, то есть появляется ЭДС в замкнутой цепи.
Данная ЭДС называется контактная ЭДС.
Если оба контакта термоэлемента находятся при одной и той же температуре, то и контактная, и объёмная термо-ЭДС исчезают.
Дата добавления: 2015-02-23; просмотров: 1320;
