Индуктивная катушка в цепи синусоидального тока
Сначала рассмотрим идеальную индуктивную катушку, активное сопротивление которой равно нулю. Пусть по идеальной катушке с индуктивностью L протекает синусоидальный ток 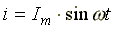 . Этот ток создает в индуктивной катушке переменное магнитное поле, изменение которого вызывает в катушке ЭДС самоиндукции
. Этот ток создает в индуктивной катушке переменное магнитное поле, изменение которого вызывает в катушке ЭДС самоиндукции
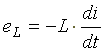 (6.9)
(6.9)
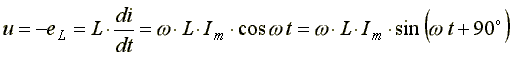 (6.10)
(6.10)
Таким образом, ток в индуктивности отстает по фазе от напряжения на 90o из-за явления самоиндукции. В реальной катушке, имеющей активное сопротивление R, ток отстает по фазе от напряжения на некоторый угол φ (0o < φ < 90o), величина которого зависит от соотношения R и L.
Полное комплексное сопротивление индуктивной катушки 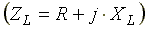 ;
;
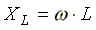 - индуктивное сопротивление
- индуктивное сопротивление
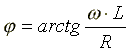 - начальная фаза комплексного сопротивления.
- начальная фаза комплексного сопротивления.
Полное сопротивление индуктивной катушки или модуль комплексного сопротивления
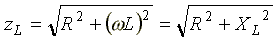 .
.
Реальной катушке соответствует векторная диаграмма (рис.6.5).
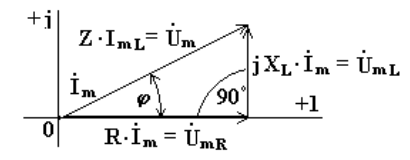
Рис. 6.5
Из анализа диаграммы видно, что вектор напряжения на индуктивности опережает вектор тока на 90o.
В цепи переменного тока напряжения на участках цепи складываются не арифметически, а геометрически.
Если мы поделим стороны треугольника напряжений на величину тока Im, то перейдем к подобному треугольнику сопротивлений (рис. 6.6).
Из треугольника сопротивлений получим несколько формул:
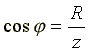 ;
; 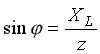 ;
; 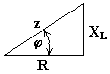
Рис. 6.6 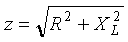 ;
;
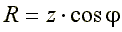 ;
; 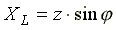 .
.
Дата добавления: 2015-02-23; просмотров: 1028;
