Пластическом деформировании металлов.

В основе всех процессов деформирования лежат напряжения, возникающие в металле. Напряжение - это мера интенсивности сил, действующих на площади какой- либо поверхности тела. Определяется оно как отношение

для растяжения (сжатия)

s= DP/ Df или s= dP/ df , (5-1)

где DP, dP - элементарная сила, действующая на элементарную площадь Df, df;

для кручения, изгиба

t= М/ W, (5-2)

где М - крутящий, изгибающий момент; W- соответствующая геометрическая характеристика сечения (геометрический момент сопротивления).

В общем случае полное напряжение направлено под некоторым углом к элементарной площади, и поэтому может быть разложено на две составляющие: нормальное напряжение s, действующее перпендикулярно площадке, и касательное напряжение t, действующее в плоскости элементарной площадки.

Если же рассматривать напряжения, действующие в объеме, то для декартовой системы 3-х координатных осей X, Y, Z проекции полного напряжения на каждую из координатных осей приводят к 3-м нормальным напряжениям s_х , s_y , s _z и шести касательным напряжениям t_yx , t_zx , t_xy , t_zy,, t_xz , t_yz .

Совокупность этих девяти напряжений характеризует напряженное состояние рассматриваемого элементарного объема и описывается следующим тензором напряжений

s_х , t_xy , t_xz

T_н = . s_y , t_yz , (5-3)

_{. .} s _z

Выбрав соответствующим образом координатные оси этот тензор можно упростить.

s₁ , 0 , 0

T_н = 0 s₂ , 0 . (5-4)

0 0 s₃

где s₁ - означает наибольшее; s₂ - наименьшее, а s₃ промежуточное главное напряжение.

Наибольшие касательные напряжения действуют на площадках, наклоненным к главным под углом 45°. Эти напряжения называются главными касательными напряжениями, величина которых определяется из формул

t₁₂= 0,5(s₁- s₂); t₂₃= 0,5(s₂- s₃); t₃₁= 0,5(s₃- s₁). (5-5)

На площадках, где действуют главные касательные напряжения, действуют и главные нормальные напряжения.

В теории пластичности введены в рассмотрение октаэдрические напряжения, действующие на плоскостях октаэдра, грани которого одинаково наклонены к 3-м главным осям напряжений. Так,

s_окт= (s₁+ s₂+ s₃)/3, (5-6)

t_окт= (2/3)(t²₁₂+ t²₂₃+ t²₃₁)^1./2= (1/3)[(s₁- s₂)²+ (s₂- s₃)²+ (s₃- s₁)²]^1/2.

Если рассматривать напряжения, действующие по случайным (не главным) ортогональным площадкам, то можно записать

t_окт = (1/3)[(s_z- s_y)²+ (s_y- s_z)²+ (s_z- s_x)² +6( t²_xy + t²_zx,+ t²_yz )]^1/2 . (5-7)

В теории пластичности иногда t_окт называют интенсивностью касательных напряжений и обозначают t_i .

Образование остаточных деформаций в металлах происходит сдвигом частиц друг относительно друга. Одно из наиболее ранних условий пластичности, сформулированное Сен-Венаном, устанавливает, что пластическое состояние тела наступает тогда, когда максимальное касательное напряжение, действующее по наиболее опасным площадкам., достигает определенного значения, равного

max {çt ê}= k.. (5-8)

Поскольку max {çt ê} является абсолютной величиной одного из 3-х главных касательных напряжений,то

çt₁₂ ê= (s₁- s₂)/2; çt₂₃ ê= (s₂- s₃)/2; çt₃₁ê= (s₃- s₁)/2 .

Эти условия иногда описывают выражением [10]

t_max= (s₁- s₃)/2. (5-9)

Величина, именуемая “интенсивностью напряжения”, “эквивалентное напряжение”[10], связана с t_i соотношением

s_i= 3t_i/(2)^1/2= (2)^-1/2[(s₁- s₂)²+ (s₂- s₃)²+ (s₃- s₁)²]^1/2

или

s_i= (2)^-1/2[(s_z- s_y)²+ (s_y- s_х)²+ (s_z- s_x)² +6( t²_xy + t²_zx,+ t²_yz )]^1/2. (5-10)

Формула (5-10), как показали экспериментальные исследования, применима к оценке предельных состояний пластичных материалов и дает результаты, менее удовлетворительные для материалов, неодинаково сопротивляющихся растяжению и сжатию.

Если в пределах упругих деформаций справедлив закон Гука s= Еe , то в сложном напряженном состоянии закон Гука может быть записан в форме [10]

s_i = Е^¢e _i , (5-11)

где Е^¢- функция деформации e или Е^¢ =ds_i /de;

e_i= 2^-0,5(1+m)^-1[(e_y- e_z)²+ (e_z- e_x)²+ (e_x- e_y)²+ 1,5(g²_yz+ g²_zx+ g²_xy)] ^1/2- интенсивность деформаций; m- коэффициент Пуассона; g_yz , g_zx , g_xy- относительные углы поворота сечений.

Губером и Мизесом было предложено другое условие, согласно которому пластическое состояние тела наступает в тот момент, когда интенсивность напряжений достигает определенного значения k, постоянного для каждого деформируемого материала, т.е. когда s_i= k.

Согласно этому условию пределы текучести на растяжение и сдвиг связаны зависимостью

k= t_т= 3^1/2 s_т. (5-12)

Если металл находится при всестороннем сжатии или растяжении, то в этом случае отсутствуют касательные напряжения, а материал деформируется лишь упруго. При всестороннем сжатии не может произойти разрушения, а при всестороннем растяжении разрушение происходит как хрупкое.

Исследования показали, что сопротивление металлов зависит от скорости деформирования и температуры в зоне деформации. При растяжении скорость деформирования характеризуется выражением v_д = de / dt , где e - относительное удлинение (истинная деформация). Следует отметить, что скорость деформирования не совпадает со скоростью движения деформирующего инструмента, а при равной скорости приложения нагрузки будет тем большей, чем меньшими являются длина или высота, или толщина деформируемого объема металла.

Отмеченное явление имеет разные объяснения. Так, Кузнецовым В.Д.[16] отмечается, что пластическая деформация сопровождается упрочнением и отдыхом. Упрочнение не зависит от температуры и определяется лишь степенью деформации. Скорость отдыха же зависит от температуры, а при постоянной температуре определяется временем отдыха и величиной, полученного упрочнения. Следовательно, в случае низкой v_д для отдыха будет достаточно времени, часть упрочнения успеет сняться отдыхом и сопротивления пластическому деформированию будут снижены. При высокой v_д отдых успеет совершиться лишь в незначительной степени, а большая часть упрочнения сохранится и сопротивление останется высоким.

В работе [2] отмеченное явление объясняется тем, что при большой скорости деформации процесс рекристаллизации не успевает завершиться. Поэтому при высоких скоростях вследствие ухудшения пластических свойств может произойти разрушение металла.

Связь касательных напряжений Клушин М.И.[17] аппроксимирует выражением

t= Cvⁿ_д, (5-13)

где С, n - экспериментально определенные коэффициенты.

Клушин М.И. дает следующие выводы:

1. Изменения скорости деформирования вызывает тем более интенсивные изменения сопротивления деформированию, чем ниже температура плавления металла.

2. При повышении скорости деформирования сопротивление деформированию возрастает не пропорционально скорости, а значительно медленней последней. Влияние скорости деформирования на сопротивление уменьшается с увеличением v_д .

3. Влияние v_д возрастает с увеличением температуры испытания, однако медленнее для металлов с высокой температурой плавления и быстрее для металлов с низкой температурой плавления.

При снижении температуры испытаний ниже нуля у поликристаллических хладноломких металлов интенсивно повышается начальный предел текучести, но упрочнение при этом мало меняется.

Гибка

Гибка является основой многих технологических процессов: вальцовки обечаек, проката труб, штамповки и т.п..

Различаются следующие виды изгиба: объемный пластический изгиб, линейный пластический изгиб, линейный чистопластический изгиб, линейных упругопластический изгиб без упрочнения, многократный пластический изгиб.

Объемный пластический изгиб.

Исходные положения:

напряженное состояние при чистом изгибе широкого бруса характеризуется наличием главных нормальных напряжений в 3-х взаимно перпендикулярных направлениях: тангенциальном s_q, аксиальном s_z , и радиальном s_r . Деформация по ширине отсутствует, и напряжение s_z поэтому является средним главным напряжением [18].

Оно равно s_z= (s_q + s_r)/ 2. Уравнение пластичности для этого случая выразится в форме

s_q - s_r= s_i = fs , (5-15)

где f - некоторый коэффициент; s - сопротивление деформированию при соответствующей степени деформации и линейной схеме напряженного состояния.

Если изгиб производится в горячем бруске, то s - есть напряжение в шейке растягиваемого участка, а при материале, деформирующемся с упрочнением

s= s_т+ П₂e . (5-16)

Если рассматривать упругий изгиб, то в нейтральном слое нормальные напряжения и деформации равны нулю, выше нейтрального слоя тангенциальные напряжения, направленные по окружности, являются растягивающими, а ниже - сжимающими. Нейтральный слой совпадает со слоем, проходящим через центр тяжести поперечного сечения бруса.

При пластическом изгибе указанные слои не совпадают друг с другом и с центром тяжести, а уравнения пластичности

для наружной зоны записываются в форме

s_qн= f [s_т + П₂ln(R_y/r)]+ s_rн, (5-17)

для внутренней зоны

s_qн= f [-s_т + П₂ln(R_y/r)]+ s_rн, (5-18)

Из-за радиальных напряжений тангенциальные напряжения в растянутой зоне уменьшаются к нейтральному слою, а в сжатой зоне увеличиваются и нейтральный слой смещается по отношению среднего слоя к центру кривизны. С увеличением кривизны изгиба радиальные напряжения непрерывно возрастают, приводя к увеличению смещения нейтрального слоя во внутреннюю зону и т.д. Достаточно наглядно это показано на рис. 5.4.

Если объемно пластический изгиб происходит с упрочнением или без упрочнения, то выражения для определения геометрических параметров гиба будут разными. При этом явления, свойственные пластическому изгибу заметно проявляются при радиусах гиба, меньших 3, т.е при r = r /h< 3 , где h= R_н- R_в - высота бруса. Во время такой пластической деформации уменьшается высота бруса, но увеличивается длина и возможно возрастание ширины.

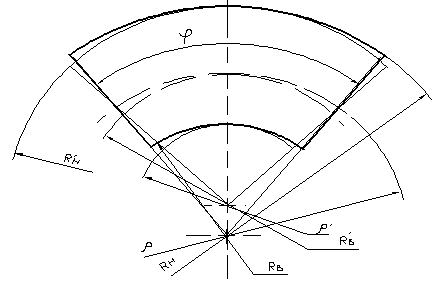
Рис.5.4

Схема деформаций бруса при объемном пластическом изгибе:

R_н, R_в, r - соответственно, радиусы наружной, внутренней поверхностей и нейтрального слоя при упругой деформации; R¢_н, R¢_в , r¢- соответственно, ра-диусы наружной, внут-ренней поверхностей и нейтрального слоя при объемном пластическом изгибе.

Изгибающий момент при объемном пластическом изгибе для плоского деформированного состояния прямоугольного бруса записывается

при наличии упрочнения

M= 1,15*1,5W{s_тh²+ П₂[(r²_н+ r²_в)ln((r_н/ r_в)- r_о)}, (5-19)

без упрочнения- то же, но при П₂ = 0. Здесь h- относительная высота бруса; W- геометрический момент сопротивления сечения бруса.

В последнем случае изгибающий момент для прямоугольного сечения бруса равен

М= 1,5Ws_т . (5-20)

Линейный пластический изгиб

При больших радиусах гиба r > (3-5) может быть принята упрощенная схема напряженно- деформированного состояния,- линейная, при которой учитываются только тангенциальные напряжения и деформации, а изгибаемый брус рассматривается прямолинейным. Здесь в рассмотрение введены чистопластический изгиб с упрочнением, упругоспластический изгиб без упрочнения, чистопластический изгиб без упрочнения. Распределение напряжений в сечении бруса для указанных случаев показано на рис. 5.5.

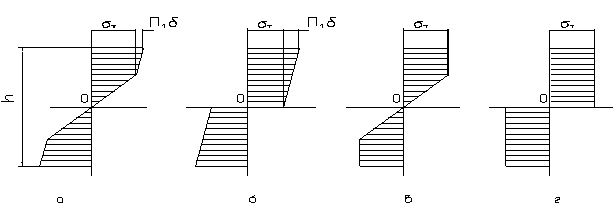
Рис. 5.5 Распределение напряжений по высоте бруса при линейном пластическом

изгибе:

а)- упругопластический с упрочнением; б)- чистопластический с упрочнением;

в) упругопластический без упрочнения; г)- чистопластический без упрочнения.

После завершения процесса гиба и прекращения действия сил происходит пружинение бруса, т.е. некоторая обратная деформация в пределах теории упругости.

В общем случае для малоуглеродистой стали величина изгибающего момента в начале пластического изгиба составляет

M» akWs_т , (5-21)

где a- коэффициент, учитывающий начальное повышение изгибающего момента (для стали 1, 2 a = 1,2; для стали 20, 25, 3 - a = 1,1); k - коэффициент профиля (для плосколежащего двутавра k = 1,8).

Линейный чистопластический изгиб с упрочнением

Было установлено, что при rs_r/E < 0,25 (r< 200 для малоуглеродистой стали) изгиб можно рассматривать изгиб как чистопластический. Тогда зависимость напряжений от координаты y выражается соотношением

s= s_т + (П₁ / R)y. (5-22)

Тогда изгибающий момент можно вычислить по выражению

M= mWs_т , (5-23)

где m - коэффициент, учитывающий профиль и эффект упрочнения.

Остаточные напряжения определяются из сложения напряжений, действующих в конечный момент изгиба, и условных напряжений разгрузки.

Условные напряжения слоя, находящегося на расстоянии y от нейтрального слоя, определяются по выражению

s¢ = y M/ J= 2ms_тy/h. (5-24)

Здесь J- геометрический момент инерции сечения.

При чистопластическом изгибе остаточные напряжения в крайних слоях зависят только от профиля сечения ( для прямоугольного s_ост= 0,5 s_т , для круглого - s_ост= 0,7 s_т ). В нейтральном слое независимо от профиля они близки к пределу текучести.

В согнутом брусе имеют место высокие остаточные напряжения, которые могут при определенных условиях вызвать коробление согнутой детали или содействовать возникновению трещин при последующей сварке.

Линейный упругопластический изгиб без упрочнения

При начальных радиусах r ³ 100- 200 параметры процесса можно определять как упругопластический без упрочнения.

Во время изгиба на бо¢льшие радиуса пружинение согнутого бруса значительно.

Изгибающий момент можно определить с помощью выражения

M= k₁Ws_т , (5-25)

где k₁ - коэффициент, учитывающий профиль сечения.

Напряжения в конечный момент изгиба в пластической зоне равны пределу текучести.

Наибольшие остаточные напряжения возникают при расстоянии от нейтрального слоя, равном y=h/2 и y=y_т , где начинается пластическая деформация.

Работа деформирования при пластическом изгибе.

Полная работа изгиба бруса длиной L выражается соотношением

A= L 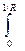M_yd(1/R_у ), (5-26)

где M_y - текущий изгибающий момент; 1/R_у - кривизна.

Многократный пластический изгиб

Деформирование посредством многократного пластического изгиба широко применяется при технологических процессах гибки, правки. В этих процессах имеют место многократные последовательный изгиб, знакопеременный изгиб прямого бруса, знакопеременный изгиб изогнутого бруса.

Многократный последовательный изгиб.

Изгиб сначала производится на большой радиус. Затем деталь гнется при ступенчато уменьшающемся радиусе гиба до получения заданной геометрии.

Величина изгибающего момента при повторных изгибах быстро достигает величины момента, соответствующей изгибу на суммарную кривизну. Промежуточные разгрузки детали не влияют на величину изгибающего момента, зависящую как и при простом изгибе от конечного радиуса.

Такой процесс обычно происходит при холодной деформации.

Многократный знакопеременный изгиб прямого бруса.

Изгиб, например, в процессе правки детали, производится на один радиус в противоположные стороны.

Конечные величины изгибающих моментов равны конечной величине изгибающего момента первого изгиба на суммарную кривизну и степень упрочнения материала не зависит от количества изгибов.

Многократный знакопеременный изгиб изогнутого бруса.

При многократных знакопеременных изгибах на малую кривизну выравниваются механические свойства материала, получившиеся от распрямления начальной кривизны.

Поперечный пластический изгиб.

В отличие от чистого изгиба, при поперечном на брус действуют изгибающий момент, непрерывно меняющийся по длине бруса, и поперечные и продольные силы. Продольные силы могут быть как сжимающими, так и растягивающими. Эпюры распределения нагрузки приведены на рис. 5.6.

На контактных участках бруса контактные напряжения вызывают перераспределение нормальных и касательных напряжений. В сжатой зоне (внутренняя зона поперечного сечения) значительно возрастают нормальные сжимающие напряжения во всех взаимно перпендикулярных направлениях, из-за чего повышается изгибающий момент, необходимый для изгиба контактного участка бруса. Продольные силы также вызывают перераспределение нормальных и касательных напряжений по высоте бруса.

У брусьев сложного профиля (трубы, уголки, швеллеры и т.п.) касательные напряжения возникают и в двух других взаимно перпендикулярных плоскостях.

Напряженному состоянию бруса произвольного сечения соответствует уравнение пластичности (5-11).

Рассмотрим некоторые особенности пластического изгиба, важные для технологического процесса гибки.

Поперечный пластический изгиб при большом расстоянии между опорами.

В этом случае, когда касательные напряжения незначительны, считаются справедливыми зависимости, выведенные для чистого изгиба.

Здесь сначала происходит упругий изгиб с переменной кривизной по его длине; затем на участке приложения внешней силы, где изгибающий момент достигает максимума, в крайних по высоте поперечного сечения слоях бруса, возникают пластические деформации, в дальнейшем распространяющиеся в обе стороны и к его середине. С увеличением кривизны изгиба пластические зоны охватывают все больший объем изгибаемого бруса.

Поперечный пластический изгиб при малом расстоянии между опорами.

В этом случае касательные напряжения оказывают в ряде ситуаций существенное влияние на характер деформации изгибаемого бруса и на параметры процесса. Здесь процесс можно рассматривать как чистопластический и как упругопластический с упрочннением и без него.

При упругопластическом изгибе прямоугольного бруса с упрочнением касательные напряжения в пластической зоне имеют наибольшее значение в слое, граничащем с упругодеформированной зоной, где они равны t= 0,15t_т.

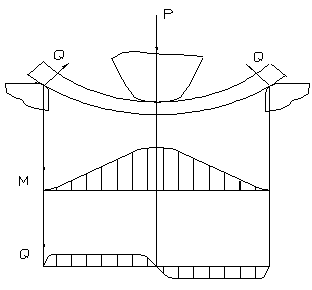
Рис. 5.6

Распределение изгибающего момента и поперечной силы при поперечном пластическом изгибе.

В процессе чистопластического изгиба с упрочнением прямоугольного бруса касательные напряжения на нейтральном слое равны

t= 0,15t_т при относительном расстоянии между опорами l= 5...6. У тонкостенного кольцевого сечения, касательные напряжения будут достигать на нейтральном слое значений t= t_т при большем расстоянии между опорами. В средней зоне бруса касательные напряжения достигают максимума, а нормальные напряжения снижаются здесь до минимума.

При чистопластическом изгибе прямоугольного бруса с относительным расстоянием между опорами l< 6...12 вследствие одновременного действия нормальных и касательных напряжений влияние последних будет сказываться на параметрах процесса.

При одновременном действии нормальных и касательных напряжений эпюра нормальных напряжений будет соответствовать эпюре интенсивности напряжений.

Проявление действия касательных напряжений может быть нескольких видов. Если эти напряжения превосходят предел текучести в средних слоях только на небольшом участке по длине бруса, где кривизна изгиба достигает предельной величины, то на этом участке произойдет незначительный сдвиг, т.к. соседние по длине участки будут препятствовать развитию деформации сдвига. При многих технологических процессах гибки у изгибаемой заготовки имеются концы, остающиеся прямыми. Они оказывают тормозящее действие на деформацию сдвига, являясь жесткими участками. При достаточной длине прямых концов незначительные деформации сдвига локализуются на небольших участках.

При гибке в роликах или по шаблону соседние участки бруса, недеформируемые в рассматриваемый момент, так же как и прямые концы, предупреждают деформацию сдвига; значительные деформации сдвига могут произойти только при изгибе крайних участков заготовки.

Если касательные напряжения достигают предела текучести по всей длине бруса, то пластический сдвиг получится вдоль всего бруса, причем наибольшее искривление получат его торцевые плоскости. Если, в этой связи, сгибать длинную трубу, то в наружных слоях в месте изгиба возникнут чрезмерно большие деформации растяжения, из-за чего произойдет разрыв заготовки.

В случае изгиба бруса с прямыми концами расстояние между опорами сокращается до весьма малых размеров, то при достижении поперечной силы максимального значения произойдет местный сдвиг по перечным плоскостям.

Гибка профилей в том числе труб производится на специальных станках (см. рис. 5.1,е)

При гибке труб должны выполняться следующие параметры:

1. Радиус гиба. Отношение R/d.

Рис. 5.7 Деформация сечения уголка (а), трубы (б).

Рис.5.8 Деформации по длине

а) уголка; б) трубы; в) двутавра.

2. Овальность a= 200(d_max- d_min)/( d_max+ d_min), %. ( а= 6- 12% для АЭС). Отклонения толщины стенки

b= 100%(s₁- s₂)/s₁ должны соответствовать требованиям чертежа.

3. Гофры не должны превышать допустимых пределов.

4. Угол загиба должен соответствовать конструкторской документации.

Для предотвращения недопустимых деформации (см. рис.5.7, 5.8) профилей используют специальные оправки; соответствующий профиль ручьев.

Гибка листов производится способом, показанным на рис. 5.1,д.

В валках могут гнуть как цилиндрические обечайки, так и конические. Во время гибки заготовки с остаточной кривизной прогиб ее в валках будет несимметричным. При сходе с переднего бокового валка участок заготовки постепенно, по мере перемещения к среднему валку, нагружается изгибающим моментом, постепенно возрастающим. Во время соприкосновения этого участка со средним валком происходит пластический изгиб, и кривизна участка достигает максимума. После продвижения за средний валок кривизна участка из-за пружинения уменьшается, но незначительно. Следовательно, по одну сторону среднего валка кривизна изменяется от нуля до максимума, а по другую - остается примерно постоянной, равной наибольшей величине.

Наибольшая кривизна заготовки за один пропуск лимитируется тяговым усилием, которое ограничивается условием сцепления приводных валков с заготовкой Т_мах= Р_хm, где Р_х - суммарное усилие на приводном валке; m, - коэффициент трения скольжения валков по изгибаемой заготовке. На величину m оказывают сильное влияние окалина, ржавчина и т.п. Усилие на среднем валке для симметричной машины равно

Р_ср = 2М/ [(R+ s/2)tga,

где R - радиус обечайки по средней линии; a- угол воздействия силы F.