Теоретическое распределение.

Сбор эмпирической информации может быть осуществлен двумя путями: исследованием всей сово­купности социальных объектов, которые являются предметом изучения в пределах, очерченных программой социологического иссле­дования, и изучением лишь части этих объектов. В первом случае исследование называется сплошным, а множество социальных объектов — генеральной совокупностью, во втором исследование называется выборочным, а выделенная часть объектов — выборкой¹⁶.

Одна из основных задач статистики состоит в том, чтобы по данным выборки оценить параметры генеральной совокупности.

Гистограмма и полигон распределения, построенные на основу эмпирических данных выборки, позволяют выявить лишь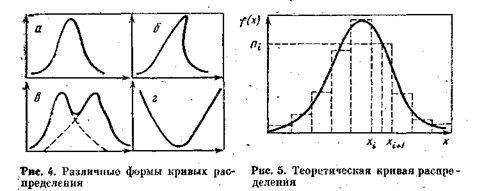

приближенную картину реального распределения в генеральной совокуп­ности.

При увеличении выборочной совокупности и все большем дроб­лении величины интервалов эмпирическое распределение в виде гистограммы или полигона все более приближается к некоторой кривой, называемой кривой распределения.

Если группировочный признак является непрерывной величиной, тo в предельном случае при, постепенном уменьшении величины интервала полигону и гистограмме будет соответствовать некоторая гладкая кривая (рис. 5).

Эта кривая распределения, являющаяся предельным случаем полигона данного эмпирического распределения, называется по установившейся терминологии кривой плотности распределения. Обозначим соответствующую функцию f(z).

В терминах теории вероятностей плотность распределения мож­но трактовать следующим образом: вероятность (р) того, что слу­чайная величина (x) примет значение из достаточно малого интер­вала (XiX_i+1), равна произведению длины интервала на высоту пря­моугольника (f(xi)), т. е.

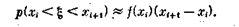
Для интервала произвольной длины суммированием этих значений получим, что

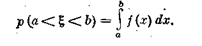
Отсюда приходим к определению фундаментального понятия теории вероятностей — функции распределения (F) случайной величины (x), которая по определению есть

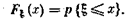
Знание функции распределения дает исчерпывающее представление о поведении совокупности в отношении изучаемого признака, поэто­му определение типа распределения признаков представляет одну из задач исследования массовых явлений.