Координати Сонця

У більшості інсоляційних розрахунків необхідно знати координати Сонця, якими є висота Сонця h і азимут А або румб Р . Ці координати на будь-який час дня і пору року можна підрахувати за формулами сферичної тригонометрії [10]:

sin h = sin Ш×sin С_x + cos Ш×cos С_x×cos ω_t ; (3.24)

sin А = cos С_x×sin ω_t/cos h , (3.25)

де Ш – географічна широта місцевості; С_х – схилення Сонця; ω_t – часовий кут ходу Сонця по небосхилу, що обчислюється як кутова величина пересування Сонця по сферичному небосхилу в градусах за формулою

ω_t = 2πt_i/T_д ,

де 2π – дорівнює 360^о; t_i – це кількість годин часу до півдня зі знаком (–) або після півдня зі знаком (+); Т_д – тривалість доби (24 години).

Як відомо [90], криві добового ходу тіні від стрижневого об’єкта певної висоти Н будуть мати різний характер залежно від пори року, як це показано безвідносно до географічної широти на рисунку 3.12.

Із рисунка 3.12 легко бачити, що довжина тіні від стрижня взимку (22.12) найдовша, весною та восени – середня, а влітку (22.6) вона найкоротша. При цьому звертаємо увагу, що на відміну від зими і літа у весняно-осінній період хід тіні від стрижневого об’єкта суттєво відмінний тим, що кінець тіні прямує вздовж прямої лінії, а це вже такий виняток, який дозволяє спростити рівняння залежності координат Сонця від часового кута ходу Сонця. Схилення Сонця при цьому дорівнює нулю (С_х = 0) і рівняння набувають такого спрощеного вигляду:

sin h = cos Ш×cos С_x ; (3.26)

sin А = sin ω_t/cos h₀ . (3.27)

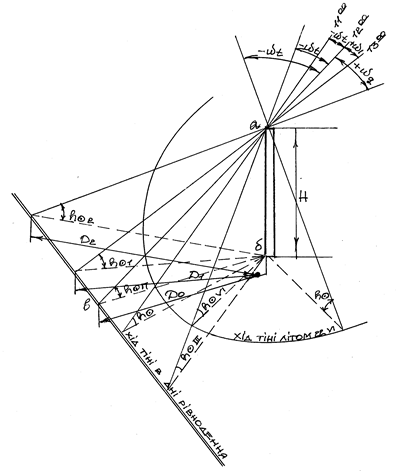
Рис. 3.12. Схема ходу тіні влітку та навесні – восени

Розглядаючи схеми (трикутники абв і абг), можна довести справедливість формули (3.24) для днів рівнодення та отримати додаткове рівняння для визначення румба Сонця Р₀ у дні рівнодення:

сos А = tg Ш×tg h . (3.28)

День рівнодення особливий ще й тим, що опівдні висоту Сонця можна спрощено визначити за такою залежністю:

h ₁₂ = (90 – Ш).

Для визначення координат Сонця в окремих випадках можна скористатись таблицями, наведеними в деяких посібниках [64]. Але ці дані не можуть дати відповіді на всі можливі випадки в практиці проектування, і тому не рідко виникає потреба обчислити координати Сонця за формулами. Це особливо стає необхідним при використанні ЕОМ для вирішення інсоляційних задач. У цих випадках для спрощення програм розв’язання інсоляційних задач потрібно мати залежності, за якими можна було б обчислити часовий кут ходу Сонця (ωt) залежно від азимута Сонця (А ):

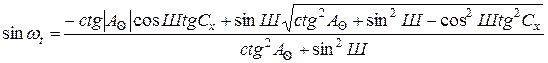, (3.29)

або, навпаки, азимут Сонця залежно лише від часового кута ходу Сонця (ωt):

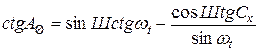, (3.30)

або обчислення азимута Сонця (А ) залежно лише від висоти Сонця (h ) на будь-який день року:

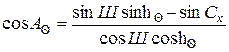. (3.31)

Легко бачити, що ці залежності значно будуть спрощені для днів рівнодення, коли схилення С_х = 0.