Краткие теоретические сведения. К электрическим свойствам, наиболее широко используемым для исследования материалов, в первую очередь

К электрическим свойствам, наиболее широко используемым для исследования материалов, в первую очередь, относятся удельная электропроводность (g) и обратная ей величина – удельное электросопротивление (r).

r = 1\ g.

Электропроводность металлов обусловлена движением свободных электронов, изменяющих свое состояние под воздействием электрического поля, что и приводит к возникновению результирующего тока. При своем движении поток электронов испытывает сопротивление, вызываемое флуктуациями тепловых колебаний атомов в решетке и ее несовершенствами.

В сплавах существенный вклад в величину удельного электросопротивления вносят межфазные границы и области концентрационной неоднородности.

Для определения удельного электросопротивления используют формулу:

r = RS\L,

где R – электрическое сопротивление, Ом;

S – площадь поперечного сечения, м²;

L – длина образца, м.

Точность определения электросопротивления зависит от точности определения размеров образца, точности измерительных приборов и установок, от колебаний температуры.

Электросопротивление металлического проводника определяют по формуле:

R_t = R₀ (1+at),

где a – температурный коэффициент,

a_R = (dR\dt) (1\R₀).

Для меди: a = 2х10^-31/°С.

Для железа: a= 4х10^-31/°С.

Метод двойного моста. Этим методом можно с высокой точностью измерять малые электросопротивления (от 10^-6 до 1 Ом). Принципиальная схема двойного моста представлена на рис. 15.1. Применение двойного моста для измерения малых электросопротивлений основано на том, что дополнительные сопротивления контактов и потенциальных токоподводов, связанных с образцом, не влияют на потенциалы точек f и c, к которым подсоединен нуль-гальванометр, поскольку величина промежуточных сопротивлений R₁, R₂, R₃, R₄ намного больше (больше 100 Ом) указанных дополнительных сообщений.

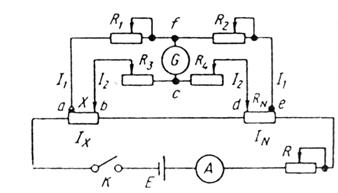
Рисунок 15.1 – Принципиальная схема двойного моста

Измерения проводят следующим образом. Изменяя сопротивление R₁–R_2, R₃–R₄ при эталонном R_N, добиваются равенства потенциалов в точках f и c, что соответствует нулевому показанию гальванометра. В этот момент равновесия моста падение напряжения на участках af и fe должно быть соответственно равно падению напряжения на участках ac и ce. Отсюда

I_xX + I₂R₃ = I₁R₁ ; I_xX = I₁R₁ – I₂R₃ ,

I_NR_N + I₂R₄ = I₁R₂ ; I_NR_N = I₁R₂ – I₂R ,

Так как I_x = I_N , то

X = R_N(I₁R₂ – I₂R₃) \ (I₁R₂ – I₂R₄),

Если R₁ = R₃ , а R₂ = R₄ , то

X = R_N (R₁\R₂).

Равенство сопротивлений R₂ и R₄ достигается в приборе тем, что их изготавливают в виде магазинов сопротивления, рычаги которых соединены друг с другом, и изменение одного сопротивления вызывает соответственно такое же изменение другого. Сопротивления R₁ и R₃ заведомо устанавливают равными друг другу.

Уравновешивание достигается регулированием величины эталонного сопротивления R_N при постоянном отношении плеч R₁/R₂ = R₃/R₄ или, напротив, сохранением в процессе измерения постоянного значения R_N и изменения отношения плеч. Более часто применяют мосты, в которых сохраняют в процессе измерения постоянное R_N, причем уравновешивание схемы достигается изменением сопротивлений R₂ и R₄, тогда как R₁ и R₃ в процессе измерения не изменяют. Высокая точность измерения по схеме двойного моста объясняется тем, что сопротивления R₁, R₂, R₃, R₄ выбирают значительно больше сопротивлений Х и R_N.

Таким образом, сила тока, проходящего через ветви afe и bcd, значительно меньше, чем сила тока, проходящего через Х или R_N. Поэтому небольшие изменения в сопротивлении этих ветвей за счет переменного сопротивления контактов и подводящих проводов мало сказываются на потенциалах точек f и c. Напротив, даже малые изменения сопротивления образцов будут отмечены. Они приведут к изменению потенциалов в точках b и d, а, следовательно, и в точке с, к которой подключен пульт нуль-гальванометра. Небольшие изменения сопротивления Х будут отражаться на показаниях гальванометра G и для получения его нулевого показания нужно изменить сопротивления R₁ и R₂.

Для проверки правильности показаний моста включают вместо измеряемого сопротивления Х известное эталонное сопротивление. Если Х¹ – сопротивление образца без подстановки эталона, а R¹_N – сопротивление эталона, то истинное сопротивление образца Х_ист может быть вычислено из соотношения

Х_ист/Х = R_N/R¹_N.

Для повышения точности схемы двойного моста применяют гальванометры зеркального типа с чувствительностью порядка 10^-8 или 10^-9 А на 1°, используя для регистрации оптическую шкалу. Силу тока выбирают в зависимости от сопротивления измеряемого образца.