Устройство экспериментальной установки и методика измерений

Экспериментальная установка (рис. 9.1) состоит из стеклянного баллона 1, соединенного с водяным манометром 2 и ручным насосом (на рис. 9.1 не показан). Посредством крана 3 баллон может соединяться с атмосферой.

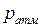Обозначим атмосферное давление во время опыта , абсолютную температуру 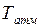(температура в комнате), объем газа (равен постоянному объему баллона) 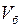, а его массу 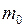. Назовем это начальным (нулевым) состоянием. При помощи насоса можно в баллон добавлять некоторое количество воздуха, и тем самым повышать его давление.

Запишем уравнение состояния идеального газа в следующем виде:

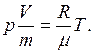
Величина 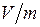называется удельным объемом. В данном эксперименте объем газа 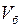остается неизменным, поэтому накачивание в баллон воздуха (увеличение его массы до значения 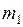) приводит к уменьшению удельного объема от 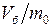до 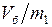. Несложно показать, что уравнение Пуассона (9.2) справедливо и для удельных объемов, т.е.

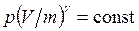(9.3)

Рассмотрим процессы, которые происходят с газом при выполнении данного эксперимента, и характерные его состояния.

При накачивании воздуха в баллон (первый процесс; рис. 9.2) внешними силами совершается определенная работа. Если процесс накачивания газа проводить быстро, то процессом теплообмена с атмосферой можно пренебречь. Поэтому данный процесс можно считать близким к адиабатическому. Следовательно, за счет работы внешних сил увеличивается внутренняя энергия газа, при этом его температура увеличивается до значения 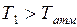, давление принимает значение 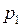, а масса станет равной 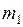(первое состояние; рис. 9.2).

После прекращения накачивания неизменная масса 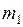изохорически охлаждается (второй процесс; рис. 9.2) до комнатной температуры 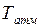за счет теплообмена с окружающей средой через стенки баллона. В конце этого процесса устанавливается второе состояние, характеризуемое давлением

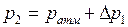, (9.4)

температурой 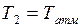и удельным объемом 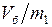. Под 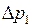понимается избыточное давление газа в этом состоянии, измеряемое с помощью манометра (второе состояние; рис. 9.2).

Теперь если быстро соединить баллон с атмосферой (третий процесс; рис. 9.2), открыв кран, воздух начнет выходить из баллона. После сравнивания давлений в баллоне с атмосферным (равенство уровней в коленях водяного манометра), кран следует закрыть. Этот процесс расширения газа, в силу выше указанных обстоятельств для первого процесса, также можно в первом приближении считать адиабатическим. При этом воздух совершает положительную работу против внешних сил (сил атмосферного давления) что, согласно первому закону термодинамики, приведет при данном процессе к уменьшению его внутренней энергии (адиабатическому понижению температуры). Установившееся третье состояние газа в конце этого процесса (третье состояние; рис. 9.2) характеризуется параметрами: давлением

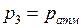, (9.5)

температурой 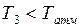и удельным объемом 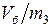( 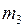– масса газа, оставшаяся в баллоне).

После этого в течение некоторого времени происходит нагревание газа (четвертый процесс; рис. 9.2) за счет теплообмена с окружающей атмосферой до ее температуры. Давление при этом несколько увеличивается на величину 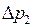, которое измеряется манометром. Новое, четвертое состояние (рис. 9.2), характеризуется параметрами: давлением 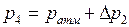, температурой 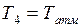, удельным объемом .

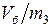Из пройденных газом выше описанных процессов и состояний (рис. 9.2) несложно рассчитать коэффициент Пуассона 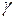. Запишем уравнение (9.3) для третьего адиабатического процесса охлаждения газа

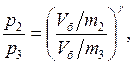
или с учетом (9.4) и (9.5)

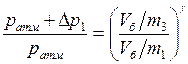. (9.6)

Используя уравнение Бойля – Мариотта (изотермический процесс 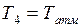) для установившихся второго и четвертого состояний, можно записать:

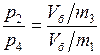. (9.7)

Из уравнений (9.6) и (9.7) следует:

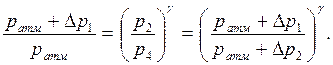
Логарифмируя выражение (9.6) получим

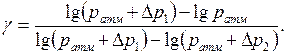
Из-за незначительного отличия давлений 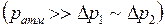, стоящих под функциями логарифмов, в первом приближении логарифмы величин можно заменить их численными значениями. В таком случае

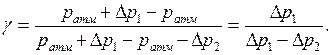
Учитывая, что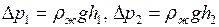

где 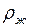=10³ кг/м³ – плотность жидкости в манометре,

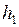и 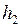– разность уровней в коленях манометра (рис. 9.1) в состояниях 2 и 4 соответственно.

Таким образом, выражение для расчета коэффициента Пуассона будет иметь вид

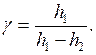(9.8)