Методика проведения измерений и описание экспериментальной установки

Изучение законов вращательного движения в настоящей работе проводится на специальной экспериментальной установке, называемой маятником Обербека. Устройство экспериментальной установки схематически показано на рисунке 6.4. Во втулке 1 со шкивом 2, свободно вращающимся вокруг горизонтальной оси, под прямым углом друг к другу закреплены четыре стержня, образующих крестовину. На стержнях закреплены винтами четыре одинаковых груза 3, массой m₁ каждый. Передвигая грузы по стержням, можно изменять момент инерции крестовины с грузами. При этом необходимо следить за тем, чтобы грузы располагались симметрично относительно оси вращения. При правильном расположении грузов крестовина в свободном состоянии должна находиться в состоянии безразличного равновесия (в противном случае при вращении на нее будут действовать переменные во времени моменты сил, которые могут исказить результаты измерений). Для сообщения крестовине равноускоренного вращения на шкив 2 навита нить 4, на свободном конце которой закреплен груз 5 массы m, которая регулируется количеством дисков-перегрузков, надетых на ось груза. Посредством неподвижной втулки 6 крестовина закреплена на вертикальной колонне 7, установленной в основании 8. На втулке 6 смонтирован также тормозной электромагнит, который при подаче на него напряжения питания, посредством фрикционной муфты удерживает маятник в состоянии покоя.

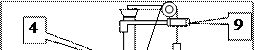На вертикальной колонне закреплены два кронштейна 9 и 10, в которых установлены фотоэлектрические датчики. Датчик верхнего кронштейна (9) при перекрывании света движущимся грузом 5 вырабатывает импульс, запускающий электронный милисекундомер, смонтированный в основании установки. Датчик нижнего кронштейна (10) в аналогичной ситуации вырабатывает импульс, останавливающий миллисекундомер и включающий тормозной электромагнит. Тем самым обеспечивается автоматическое измерение времени движения груза 5. Верхний кронштейн является подвижным, и его положение определяет высоту опускания груза 5.

На лицевой панели прибора находятся табло миллисекундомера и кнопки управления с надписями. Кнопка «Сеть» предназначена для включения и выключения установки. Кнопка «Пуск» отключает тормозной электромагнит и генерирует импульс, разрешающий измерение времени. Кнопка «Сброс» обнуляет показания миллисекундомера.

Первая часть работы заключается в экспериментальной проверке выполнения основного уравнения динамики вращательного движения – соотношения (6.11), согласно которому момент сил, приложенный к крестовине, и получаемое ею угловое ускорение должны быть пропорциональны. Рассмотрим условия движения маятника и определим величины, которые следует измерить для решения указанной задачи.

В процессе измерений на шкив маятника действует вращательный момент 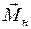, создаваемый силой натяжения нити 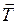. Если радиус шкива равен 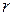, то

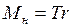. (6.12)

Пренебрегая действием сил трения, на основе уравнения (11) запишем уравнение движения маятника:

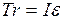. (6.13)

Сила натяжения 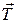может быть найдена из уравнения движения груза 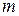с ускорением a:

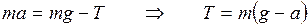. (6.14)

Ускорение движения груза можно найти, измерив время t его опускания с высоты h. Будем считать, что движение происходит из состояния покоя, и начальная скорость равна нулю. Тогда

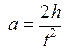и (6.15)

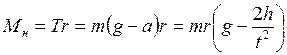. (6.16)

Угловое ускорение

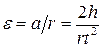. (6.17)

Таким образом, измерив величины 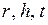при различных перегрузках m, можно построить зависимость 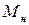( 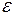), которая, в соответствии с уравнением (6.11) должна иметь вид прямой линии, причем тангенс угла наклона этой прямой равен моменту инерции крестовины.

Найдем ожидаемый вид зависимости момента инерции 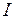крестовины от расстояний 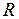грузов до оси вращения и их геометрических размеров. Очевидно, что момент инерции крестовины с грузами складывается из собственного момента инерции крестовины 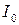(без грузов) и момента инерции грузов:

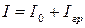. (6.18)

Поскольку все грузы имеют одинаковую массу 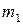, форму, размеры и находятся на одинаковом расстоянии 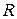от оси вращения АА (как это показано на рисунке 6.5), то, обозначив момент инерции одного груза 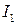, положим, что .

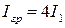Будем считать грузы однородными цилиндрами с линейной плотностью 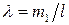. Разобьём мысленно грузы на тонкие диски толщиной 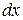. Каждый такой диск имеет массу:

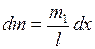
и находится на расстоянии х от оси вращения. Относительно оси 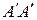, лежащей в плоскости диска его момент инерции можно найти по известной формуле:

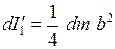
Тогда по теореме Штейнера момент инерции диска относительно оси АА можно найти по формуле:

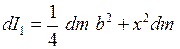. (6.19)

Интегрируя (6.19) в пределах от 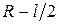до 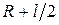, найдем:

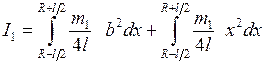. (6.20)

После алгебраических преобразований получаем:

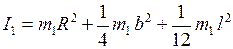. (6.21)

В целом момент инерции крестовины

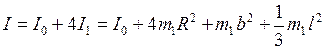. (6.22)

Поэтому график зависимости

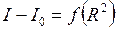(6.23)

должен представлять собой прямую, тангенс угла которой равен 4m₁, а на оси ординат эта прямая должна отсекать отрезок 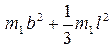. Поскольку соотношение (6.22) является прямым следствием использования теоремы Штейнера, его экспериментальная проверка эквивалентна проверке выполнения теоремы Штейнера. Сама же проверка должна заключаться в получении экспериментальных результатов, необходимых для построения графика (6.23), и сравнении полученной зависимости с теоретическими предсказаниями.