Краткая теория. В данной работе изучаются свободные незатухающие гармонические колебания, подчиняющиеся следующему закону:

В данной работе изучаются свободные незатухающие гармонические колебания, подчиняющиеся следующему закону:

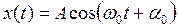, (3.1)

В этом уравнении: А – амплитуда колебаний, т.е. наибольшее отклонение маятника из положения равновесия, 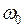– циклическая или круговая частота колебаний, t – время, 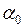– начальная фаза колебания, 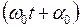– фаза колебания в момент времени t с. Периодом колебания маятника Т называют время, в течение которого маятник совершает одно полное колебание. Циклическая частота и период связаны соотношением:

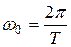. (3.2)

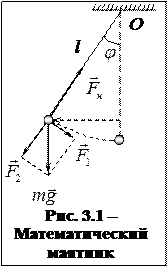Математический маятник

Математическим маятником называют идеальную систему, состоящую из невесомой и нерастяжимой нити, на которой подвешена масса, сосредоточенная в одной точке.

Отклонение маятника от положения равновесия можно характеризовать углом j, образованным нитью с вертикалью (рис. 3.1).

При отклонении маятника от положения равновесия возникает вращающий момент М, созданный силой 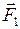, являющейся составляющей силы тяжести 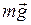. Численное значение вращающего момента равно:

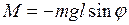, (3.3)

где m – масса,

l – длина маятника.

Уравнение динамики для вращательного движения имеет вид:

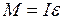, (3.4)

где I – момент инерции маятника, равный ml² (для материальной точки),

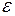– угловое ускорение, равное второй производной угла отклонения 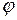по времени

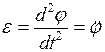. (3.5)

Приравняв выражения (3.3) и (3.4), получим

.

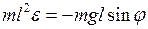Приведем уравнение к виду

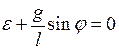. (3.6)

В случае малых колебаний 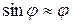и, если ввести обозначение

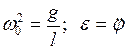, (3.7)

то получим дифференциальное уравнение второго порядка:

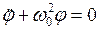. (3.8)

Оно имеет решение (сравните с 3.1)

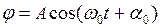. (3.9)

Из формул (3.2) и (3.7) выразим период колебаний математического маятника

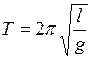, (3.10)

где l – длина математического маятника.

Полученное соотношение (3.10) может быть использовано для определения ускорения свободного падения g. Для этого необходимо измерить Т, и l и выразить через них g с помощью формулы (3.10).

Физический маятник

Физическим маятником называют тело массой m произвольной формы и размеров, свободно колеблющееся вокруг оси, не проходящей через центр тяжести (рис. 3.2).

При отклонении маятника на небольшой угол j он начнет колебаться около положения равновесия под действием составляющей 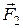силы тяжести маятника 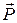. Составляющая силы тяжести маятника, направленная вдоль ОС, уравновешивается реакцией оси. Вращательный момент, стремящийся вернуть маятник в положение равновесия, равен:

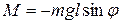
где m – масса,

l – расстояние от точки подвеса до центра тяжести.

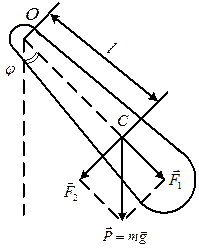
Рис. 3.2 – Физический маятник

Используя основной закон динамики вращательного движения ( 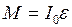) имеем:

,

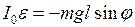где e – угловое ускорение (см. 3.3),

I₀ – момент инерции маятника относительно оси качания О.

При малых углах отклонения маятника от положения равновесия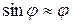

Приведем уравнение (3.9) к виду

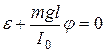
и введя обозначение

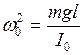, (3.11)

имеем,

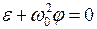, (3.12)

или

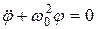. (3.13)

Частным решением дифференциального уравнения (3.13) является:

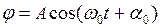, (3.14)

где 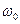- циклическая частота колебаний, равная

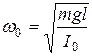. (3.15)

Период колебания

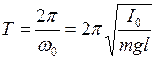. (3.16)

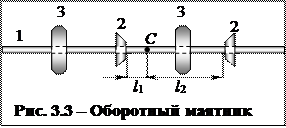Полученное соотношение (3.16) также может быть использовано для определения ускорения свободного падения g. Для этого необходимо измерить Т, I₀ и l и выразить через них g с помощью формулы (3.16). Оказывается, однако, что с высокой точностью можно измерить только период колебания Т маятника, а величины I₀ и l достаточно точно измерить не удается. Для этой цели удобно использовать оборотный маятник, т.е. маятник, представляющий собой массивный стержень (1), с двух концов которого закреплены параллельные друг другу опорные призмы (ножи) (2), за которые маятник может поочередно подвешиваться. Вдоль стержня могут перемещаться и закрепляться тяжелые грузы (3) (см. рис. 3.3).

Достоинством метода оборотного физического маятника для определения ускорения свободного падения является то, что I₀ и l не входят в расчетную формулу для g. Перейдем к обсуждению этого метода.

Согласно теореме Штейнера, момент инерции относительно оси качания О

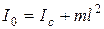, (3.17)

где I_с – момент инерции маятника, относительно оси, параллельной оси качания и проходящей через центр масс С маятника.

Подставляя (3.17) в (3.16), получаем

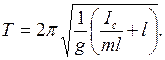(3.18)

Попробуем найти такие два положения l₁ и l₂ (l₁¹l₂) опорных призм по разные стороны от центра масс, чтобы периоды колебаний маятника совпадали:

Т(l₁) = Т(l₂).

Как видно из (3.18), для этого необходимо выполнение равенства

,

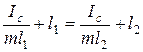которое имеет место либо при l₁=l₂, либо при

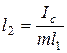. (3.19)

В последнем случае период колебаний маятника

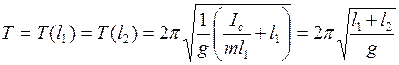. (3.20)

Следовательно, ускорение свободного падения может быть определено по формуле:

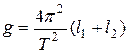. (3.21)

Как видно из (3.21), для нахождения g достаточно измерить только две величины: расстояние (l₁+l₂) между опорными ребрами призм, период колебаний маятника в положении l₁ и в «перевернутом» положении l₂, при котором l₁¹l₂. При этом периоды колебаний должны совпадать, т.е. должно выполняться равенство:

Т(l₁)=Т(l₂)=Т.

Из формул (3.8) и (3.16) видно, что математический маятник с длиной 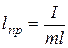будет иметь такой же период, что и физический маятник.

Величина l_пр называется приведенной длиной физического маятника. Значит, приведенная длина физического маятника – это длина такого математического маятника, у которого период совпадает с периодом колебаний данного физического маятника.