Процеси у фільтрівних центрифугах

Рушійною силою розділення у фільтрівних центрифугах, так само як і у відстійних, є відцентрова сила.

Розглянемо фільтрування у відцентровому полі. Ротор центрифуги радіусом R (рис. 5.20) заповнений рідиною, яка обертається разом з ротором з постійною кутовою швидкістю ω. Внутрішній радіус кільця рідини позначимо через r₁. Визначимо відцентрову силу dF_в для елементарного кільця з масою dm, радіусом r, товщиною dr і шириною ΔL, яка дорівнює одиниці:

dF_в=dmω²r (5.57)

Підставимо в отримане диференційне рівняння значення dm=ρ2πrdr і визначимо тиск Р_в, який виникає під дією відцентрового поля

dP_в = 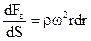, (5.58)

де dS=2πr – поверхня елементарного кільця рідини радіусом r.

Після інтегрування (5.58) у границях від r₁ до R отримаємо

Р_в=ρω² 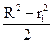(5.59)

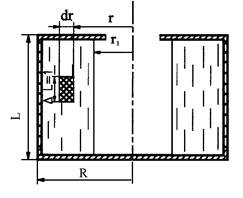
Рис. 5.20. Схема відцентрового фільтрування

Слід відмітити, що на відміну від звичайного фільтрування, процес відцентрового фільтрування здійснюється в більш складних умовах: осад і фільтрувальна перегородка мають значну кривизну, внаслідок чого фактична поверхня фільтрування змінюється вздовж радіуса, у процесі фільтрування відбувається осадження твердої фази суспензії, осад ущільнюється як під дією гідростатичного тиску рідини, яка обертається, так і масових сил самого осаду.

У фільтрівних центрифугах звичайно розділюють достатньо концентровані і грубодисперсні суспензії, тому можна припустити, що процес відцентрового фільтрування здійснюється за законом фільтрування з утворенням осаду.

Підставимо в рівняння фільтрування (4.8) величину відцентрового перепаду тисків і отримаємо з врахуванням (5.11) основне рівняння відцентрового фільтрування

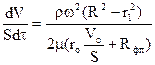, (5.60)

або після нескладних перетворень із врахуванням схеми на рис. 5.20

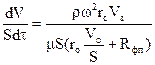, (5.61)

де r_c і V_з – середній радіус і об’єм кільця завантаження.

Рівняння (5.60) або (5.61) має назву основного рівняння відцентрового фільтрування.

Рішення рівняння (5.60) залежить від умов проведення процесу, який може здійснюватися в наступних режимах:

- при постійній різниці тисків;

- при постійній швидкості фільтрування;

- при постійних різниці тисків і швидкості фільтрування;

- при змінних різниці тисків і швидкості фільтрування;

- при заданій зміні витрат суспензії;

- при постійних витратах суспензії.

Розглянемо, як приклад, режим за постійною різницею тисків. В цьому режимі розрізняють три стадії: поступове заповнення ротора суспензією до певної границі, коли процес іде при постійних витратах суспензії (перша стадія). Потім процес продовжується при постійній різниці тисків (друга стадія), під час якої рівень суспензії у роторі підтримується незмінним. Після утворення шару осаду певної товщини подачу суспензії припиняють і починається третя стадія (при змінній різниці тисків і швидкості фільтрування), яка закінчується, коли рівень рідини досягає внутрішньої поверхні шару осаду, тобто коли починається віджимання осаду. У промисловості завантаження ротора намагаються провести як можна скоріше, а подачу суспензії припиняють, коли товщина шару рідини над осадом досягає мінімальної величини, тому сумарний час першої й третьої стадій звичайно, не перевищує 15-20% від загального часу всього періоду фільтрування, внаслідок чого процес здійснюється переважно при постійній різниці тисків.

З рівняння (5.59) випливає, що постійність статичного тиску рідини при її обертанні може бути забезпечена лише, якщо підтримується постійність рівня (r_o=const), тобто при постійному об’ємі завантаження. Тому при відцентровому фільтруванні в режимі постійної різниці тисків об’єм суспензії, який поступає в ротор за одиницю часу, повинен дорівнювати об’єму отриманого за цей час фільтрату. Приймемо. що за час першої стадії (заповнення ротора до об’єму V_з) отриманий питомий об’єм фільтрату V_1, а на перегородці утворився шар осаду h_o=V₁x_o (x_o-відношення об’єму осаду до об’єму фільтрату). Тоді основне рівняння відцентрового фільтрування приймає вигляд

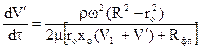(5.62)

де V^’ - об’єм фільтрату в стадії фільтрування.

Після розділення змінних, інтегрування і нескладних перетворень отримаємо залежність між об’ємом фільтрату і часом фільтрування

V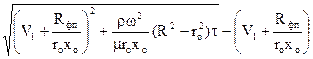^’= (5.63)