Процеси у відстійних центрифугах

В обертовому потоці на зважену частинку діє відцентрова сила, внаслідок чого вона рухається до периферії від центра вздовж радіуса із швидкістю, яка дорівнює швидкості осадження w (рис. 5.18). В той же час, частинка рухається разом із потоком з окружною швидкістю w_r. По деякій траєкторії з результуючою швидкістю w_p частинка досягає стінки (точка k), тобто осаджується.

У гравітаційному полі швидкість осадження розраховується згідно залежності

w_о = 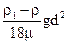. (5.42)

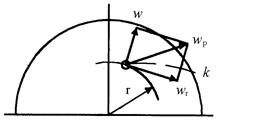
Рис. 5.18. Схема дії сил на частинку в обертовому потоці

В полі дії відцентрових сил швидкість осадження також буде залежати від густини ρ₁ і розмірів частинки d, густини рідини ρ та її в’язкості µ. Але замість сили тяжіння на частинку діє відцентрова сила, тому ми маємо підставу в останню залежність замість прискорення сили тяжіння g ввести прискорення відцентрової сили ω²r

w= 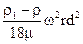, (5.43)

де r-біжучий радіус обертання частинки, ω - кутова швидкість.

Помножимо чисельник і знаменник останнього виразу на прискорення сили земного тяжіння й отримаємо

w = 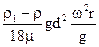(5.44)

Відношення відцентрового прискорення до прискорення сили тяжіння називається фактором розділення (або критерієм Фруда)

K_p= 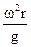(5.45)

Запишемо (5.44) у вигляді

w = w_о K_p (5.46)

Таким чином, швидкість осадження в полі відцентрових сил дорівнює добутку швидкості осадження в гравітаційному полі й фактора розділення. Фактор розділення показує - у скільки разів швидкість осадження у відцентровому полі більше швидкості осадження в полі тяжіння.

У гравітаційному полі осадження відбувається під дією сили тяжіння G_т = mg, а у відцентровому полі під дією відцентрової сили Р_в=mω²r. Цілком зрозуміло, що швидкість осадження у відцентровому полі буде більше швидкості осадження в гравітаційному полі в стільки разів, у скільки разів відцентрова сила більше сили тяжіння. Тобто ми приходимо до того ж самого виразу фактора розділення

K_p=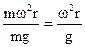

У промислових апаратах відцентрова сила перевищує силу тяжіння на два і більше порядків, отже швидкість осадження у відцентровому полі значно більше ніж у полі земного тяжіння.

Час осадження частинок у полі відцентрових сил може бути знайдений наступним чином.

Розглянемо схему горизонтальної центрифуги (рис. 5.19).

При обертанні ротора рідина у вигляді концентричного шару рухається вздовж барабана, а тверді частинки під дією відцентрової сили переміщуються до внутрішньої поверхні, утворюючи шар осаду. Швидкість осадження частинок може бути виражена диференційним рівнянням

w= ,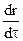

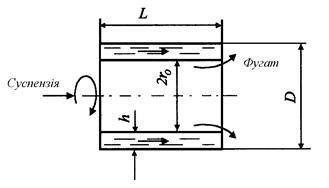
Рис. 5.19. Схема горизонтальної відстійної центрифуги

де r-шлях, який проходить частинка за час τ.

З врахуванням (5.46)

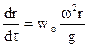(5.47)

Проінтегруємо останнє рівняння

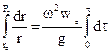, (5.48)

де R – внутрішній діаметр ротора, r_o – радіус вільної поверхні рідини, τ - час осадження.

За час осадження частинка проходить найбільший шлях R-r_o.

Після інтегрування

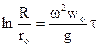, (5.49)

звідки

τ = 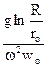. (5.50)

Таким чином, час осадження залежить від радіусів барабана і вільної поверхні рідини, частоти обертання барабана, розмірів частинок і фізичних властивостей твердої й рідкої фаз (які визначають швидкість осадження в полі сил тяжіння).

Розділювальна здатність відстійних центрифуг характеризується індексом продуктивності Σ, який визначається добутком площі циліндричної поверхні осадження S в роторі на фактор розділення K_p:

Σ = S K_p. (5.51)

Індекс продуктивності являє собою поверхню відстійника, в якому для даної суспензії досягається така ж сама продуктивність, що і в центрифузі, яка розглядається. Величина Σ відображає вплив конструктивних особливостей центрифуги на її роздільну здатність.

Розглянемо вираз для індексу продуктивності стосовно центрифуги, зображеної на рис. 5.19. Товщина шару рідини h на практиці значно менше діаметра D, тому величину фактора розділення можна віднести до середнього діаметра (D-h). Тоді відповідно з виразом (5.45)

K_p = 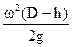(5.52)

Площа циліндричної поверхні осадження в роторі

S = π(D-h)L

Звідси

Σ = S K_p = 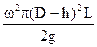(5.53)

Якщо прийняти, що рідина в роторі переміщується не по всьому кільцевому просторі, що займає шар, а тільки по тонкій внутрішній зоні кільцевого простору (поверхневий режим течії), то наближено

K_p = 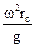і S=2πr_oL

В цьому випадку

Σ = S K_p = 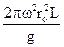(5.54)

Рівняння (5.54) можна використовувати за умови, якщо осадження твердих частинок суспензії здійснюється при ламінарному режимі. Але внаслідок значної величини відцентрової сили осадження частинок у центрифугах може відбуватися в умовах перехідного й турбулентного режимів. В цих випадках індекс продуктивності визначається наступним чином:

для перехідного режиму

Σ=S K_p ^0,715 (5.55)

для турбулентного режиму

Σ=S K_p ^0,5 (5.56)

З рівнянь (5.55) і (5.56) випливає, що в цих випадках площа відстійника, еквівалентного за продуктивністю центрифузі, що розглядається, зростає не пропорційно фактору розділення, а менш інтенсивно.