Цифро-аналоговые преобразователи

Цифровые и логические устройства по своей сути предназначены для обработки, преобразования и хранения информации. Как было отмечено выше, информационные сигналы могут быть как аналоговые, так и цифровые. Очевидно, что обработка аналоговых сигналов в цифровых устройствах без предварительного их преобразования в цифровую форму невозможна. Обработанную в цифровых устройствах информацию часто требуется преобразовать обратно в аналоговую форму. В цифровых системах ввод и вывод аналоговой информации осуществляется с помощью схем ввода-вывода, содержащих в своем составе аналого-цифровые и цифро-аналоговые преобразователи (ЦАП).

ЦАП служит для преобразования цифровой информации в аналоговую форму, т.е. выходной сигнал ЦАП в общепринятых единицах измерения тока или напряжения (мВ, В, мА) соответствует численному значению входной кодовой комбинации.

Например, при подаче на вход ЦАП кодовой комбинации (в десятичном эквиваленте), равной 150, на его выходе имеется напряжение 1500 мВ; это значит, что изменение значения входной кодовой комбинации (входного числа) на единицу приводит к изменению выходного напряжения на 10 мВ. В этом случае мы имеем ЦАП с шагом преобразования цифровой информации 10 мВ. Величина напряжения, соответствующая одной единице цифровой информации, называется шагом квантования Du_кв. При подаче на вход ЦАП последовательной цифровой комбинации, меняющейся от 0 до N, на его выходе появится ступенчато-нарастающее напряжение (рис. 5.22). Высота каждой ступени соответствует одному шагу квантования Du_кв.

5.22. Диаграмма выходного напряжения ЦАП

(N – число, соответствующее десятичному

Эквиваленту двоичного кода)

Если число входной кодовой комбинации соответствует N, то выходное напряжение U_{вых ЦАП} = N Du_кв. Таким образом можно вычислить значение выходного напряжения для любой входной кодовой комбинации. Нетрудно убедиться в том, что Du_кв является масштабным коэффициентом преобразователя, имеющим размерность тока или напряжения (так как цифровая комбинация на входе ЦАП размерности не имеет). Обычно значение Du_кв выбирают кратным десяти, что облегчает процесс пересчета соответствия преобразованного и исходного сигналов. Так как Du_кв определяет минимальное значение выходного напряжения аналогового сигнала U_{вых мин.} = Du_кв , при выборе его значения необходимо учитывать также шумовые факторы, погрешности усиления масштабирующих усилителей и компаратора.

Основные параметры ЦАП. Точность преобразования и качество работы ЦАП характеризуют следующие параметры: относительная разрешающая способность, абсолютная разрешающая способность, абсолютная погрешность преобразования, нелинейность преобразования, дифференциальная нелинейность, скорость преобразования (время одного преобразования) и максимальная частота преобразования.

1. Относительная разрешающая способность

d_о = ,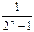

здесь n- количество разрядов двоичного числа, подаваемого на вход АЦП (n соответствует числу разрядных входов ЦАП). Относительная разрешающая способность - это обратная величина от максимального числа уровней квантования.

2. Абсолютная разрешающая способность

d_а = ,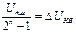

где U_пш - напряжение полной шкалы, соответствующее опорному напряжению ЦАП. Это напряжение можно считать равным максимальному выходному напряжению; 2ⁿ - 1 = N - количество ступеней квантования.

Численно абсолютная разрешающая способность равна шагу квантования Du_кв.

3. Абсолютная погрешность преобразования d_пш показывает максимальное отклонение выходного напряжения U_вых в точке пересечения с идеальной характеристикой (прямой) на уровне напряжения полной шкалы (рис. 5.21). Абсолютная погрешность преобразования оценивается в процентах или же в единицах младшего значащего разряда (МЗР). При оценке значения абсолютной погрешности преобразования знак напряжения отличия не учитывается.

4. Нелинейность преобразования ЦАП d_лн определяет максимальное отклонение реальной характеристики от идеальной (рис. 5.23) и оценивается также в процентах или в единицах младшего значащего разряда.

5. Дифференциальная нелинейность преобразования ЦАП d_дф.лн численно равна максимальной разности двух соседних приращений (шагов квантования)

d_дф.лн = Du_{кв 1} - Du_кв2.

Дифференциальная нелинейность оценивается в младших значащих разрядах и обычно не превышает нескольких единиц мзр. Он численно определяет минимальное значение выходного напряжения, т.е. квант напряжения. Для оценки дифференциальной нелинейности d_дф.лн в процентах можно воспользоваться выражением

.

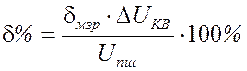Рис. 5.23. Пояснения к определению

погрешности преобразования ЦАП

Время установления выходного напряжения или тока t_уст - интервал времени от подачи входного двоичного входного кода до вхождения выходного сигнала в заданные пределы. Максимальная частота преобразования f_пр - наибольшая частота дискретизации, при которой параметры ЦАП соответствуют заданным значениям. Максимальная частота и время установления определяют быстродействие ЦАП.

Виды ЦАП условно можно разделить на две группы: с резисторными матрицами, безматричные ЦАП. В интегральном исполнении применяются только ЦАП с прецизионными резисторными матрицами, формирующими выходные сигналы путем суммирования токов.

ЦАП, как и любой преобразователь, содержит элементы цифровой и аналоговой схемотехники. В качестве аналоговых элементов используются операционные усилители, аналоговые ключи (коммутаторы), резисторные матрицы и т.д.

Аналоговые элементы, входящие в состав ЦАП, практически полностью определяют его качественные и эксплуатационные параметры, основную роль при этом играет точность подбора номиналов резисторов резисторной матрицы и параметров операционного усилителя .

При построении ЦАП и АЦП применяются аналоговые ключи, коммутирующие цепи аналоговых сигналов под воздействием управляющих логических сигналов. Токи, коммутируемые электронными аналоговыми ключами, не превышают 1,0...50 мА. Относительно высокое сопротивление открытого ключа (50 ¸ 600 Ом) требует наличия высокоомной нагрузки, что обеспечивается высокоомным входным сопротивлением ОУ.

При реализации ЦАП в интегральном исполнении большие трудности вызывает подгонка высокоточных резисторов с сопротивлениями, отличающимися по номиналам друг от друга на несколько порядков. Поэтому в интегральном исполнении применяются исключительно резистивная матрица R-2R. Когда количество разрядов ЦАП небольшое (не более восьми) и к точности преобразования предъявляются менее жесткие требования, можно использовать матрицу резисторов R-2ⁿR. Схема ЦАП, использующая последний тип матрицы, проще в изготовлении и может найти широкое применение в развитии технического творчества обучающегося.

В качестве примера рассмотрим четырехразрядный ЦАП, использующий схему суммирования токов на ОУ (рис. 5.24).

Рис. 5.24. Схема простейшего ЦАП: ЭК – электронные ключи; 0р, 1р, 2р, 3р – соответствующие разряды цифровых входов управления

Относительная разрешающая способность рассматриваемого ЦАП:

d_о = 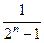= 0,0625.

Абсолютная разрешающая способность определяется при известном значении опорного напряжения U_оп. Наиболее удобными значениями U_оп являются напряжения, кратные степени двойки, т.е. 10,24 В, 5,12 В, 2,56 В и т.д.

Если принять значение опорного напряжения равным 10,24 В, то абсолютная разрешающая способность (DU_кв) определяется как

DU_кв=0,0625 × 10,24 = 0,625В.

Сопротивление резистора в цепи ключа, управляемого старшим разрядом двоичного кода, должно быть в два раза больше сопротивления резистора обратной связи R_ос. Сопротивление каждого последующего меньшего разряда в два раза больше, чем сопротивление соседнего старшего разряда. Отсюда следует, что с увеличением количества разрядов цифрового входа ЦАП резко увеличивается соотношение сопротивлений резисторов нулевого и самого старшего разрядов (R₀=2ⁿR_n)

R₀/R_n=2ⁿ = T.

Если n=8, то это отношение составляет 256 и т.д. Увеличение Т может привести к чрезмерному увеличению сопротивления резистора младшего разряда или же к сильному уменьшению номинала резистора самого старшего разряда. Поэтому ЦАП с резистивной матрицей R-2ⁿR применяется при небольшом количестве разрядов цифрового входа (при n<8). При больших Т затруднительным становится также изготовление резистивных матриц в интегральном исполнении. Известно, что номиналы резисторов в интегральном исполнении не должны превышать 50...100кОм. Поэтому, в ЦАП, выполненных по интегральной технологии, в основном применяются резистивные матрицы R-2R. Функциональная схема ЦАП с матрицей R-2R показана на рис. 5.25.

Рис. 5.25. Схема ЦАП с резистивной матрицей R–2R

Напряжение на выходе ЦАП (рис. 5.25) определяется как

= .

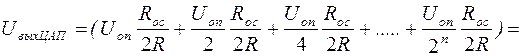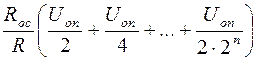Чтобы выполнить условие формирования выходного напряжения в соответствии с двоичным кодом входного числа, необходимо получить равенство R_ос=R, тогда

U_выхЦАП= U_оп .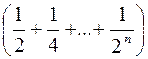

Дробные члены суммы играют роль весовых коэффициентов, а шаг квантования определяется отношением DU_кв=U_оп/2ⁿ. На рис. 5.25 символы “0” и “1” возле электронных ключей указывают на состояние ключа при подаче на цифровые входы ЦАП логического “0” или “1” соответственно.

Промышленностью ЦАП выпускается в виде интегральной микросхемы и содержит в своем составе резистивную матрицу R-2R. Схема ЦАП, построенного на базе ИМС К572ПА1, показана на рис. 5.26. В последнем случае выходные уровни, соответствующие сигналам уровня логической “1”, должны быть повышены путем соединения выходов ТТЛ инверторов с источником питания 5 В через резисторы сопротивлением 2¸10 кОм. Непосредственное согласование входных управляющих уровней ЦАП с параметрами сигналов интегральных микросхем ТТЛ-логики можно достичь путем уменьшения напряжения питания ЦАП до 5 В. Однако при этом возрастает погрешность ЦАП.

Рис. 5.26. Схема ЦАП на микросхеме КР572ПА1

Наиболее распространенными являются ЦАП серий микросхем 572, 594, 1108, 1118 и др.

\