Классификация фильтров по виду их амплитудно-частотных характеристик

Фильтры нижних частот. Для фильтров нижних частот (ФНЧ) характерно то, что входные сигналы низких частот, начиная с постоянных сигналов, передаются на выход, а сигналы высоких частот задерживаются. На рис. 12.1,а показана характеристика идеального (не реализуемого на практике) фильтра (ее иногда называют характеристикой типа «кирпичная стена»). На других рисунках представлены характеристики реальных фильтров.

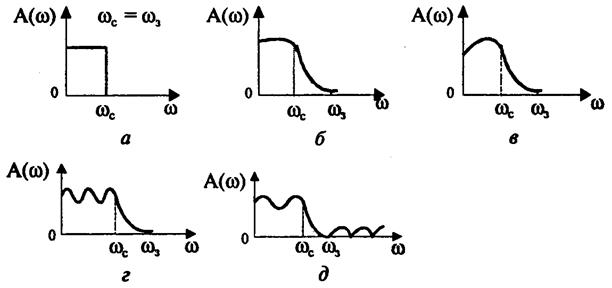
Рис. 12.1.Амплитудно-частотные характеристики

фильтров нижних частот

Полоса пропускания лежит в пределах от нулевой частоты до частоты среза ω_с. Обычно частоту среза определяют как частоту, на которой величина А(ω) равна 0,707 от максимального значения (т. е. меньше максимального значения на 3 дБ).

Полоса задерживания (подавления) начинается от частоты задерживания ω_з и продолжается до бесконечности. В ряде случаев частоту задерживания определяют как частоту, на которой величина А(ω) меньше максимального значения на 40 дБ (т. е. меньше в 100 раз).

Между полосами пропускания и задерживания у реальных фильтров расположена переходная полоса. У идеального фильтра переходная частота отсутствует.

Фильтры верхних частот. Фильтр верхних частот характерен тем, что он пропускает сигналы верхних и задерживает сигналы нижних частот.

На рис. 12.2,а приведена идеальная (нереализуемая) амплитудно-частотная характеристика фильтра нижних частот, а на рис. 12.2,б – одна из типичных реальных. Через ω_с и ω_з обозначены частоты среза и задерживания.

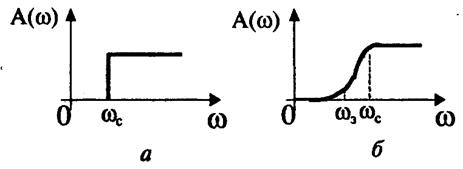
Рис. 12.2. Амплитудно-частотные характеристики

фильтров верхних частот

Полосовые фильтры (полосно-пропускающие). Полосовой фильтр пропускает сигналы одной полосы частот, расположенной в некоторой внутренней части оси частот. Сигналы с частотами вне этой полосы фильтр задерживает.

На рис. 12.3,а приведена амплитудно-частотная характеристика идеального (нереализуемого) фильтра и одна из типичных реальных характеристик (рис. 12.3,б). Через ω_с1 и ω_с2 обозначены две частоты среза, ω₀ – средняя частота. Она определяется выражением

.

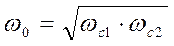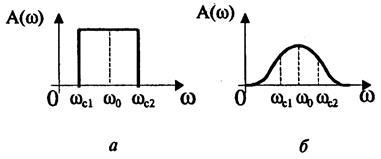
Рис. 12.3. Амплитудно-частотные характеристики полосового фильтра

а-идеальная характеристика; б-реальная характеристика

Режекторные фильтры (полосно-заграждающие). Режекторные фильтры не пропускают (задерживают) сигналы, лежащие в некоторой полосе частот, и пропускают сигналы с другими частотами.

Амплитудно-частотная характеристика идеального (нереализуемого) фильтра приведена на рис. 12.4,а. На рис. 12.4,б показана одна из типичных реальных характеристик.

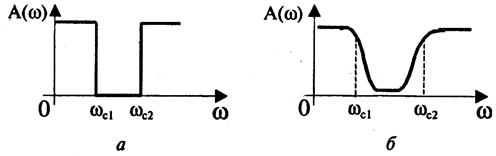
Рис. 12.4. Амплитудно-частотные характеристики

режекторного фильтра

Всепропускающие фильтры (фазовые корректоры). Эти фильтры пропускают сигналы любой частоты. Такие фильтры используются в некоторых электронных системах для того, чтобы изменить с той или иной целью фазочастотную характеристику всей системы (рис. 12.5).

Рис. 12.5. Амплитудно-частотная характеристика

всепропускающего фильтра

Классификация фильтров по передаточным функциям на примере фильтров низкой частоты. На практике широко используются фильтры, отличающиеся характерными особенностями амплитудно-частотных характеристик. Это фильтры Баттерворта, Чебышева, Бесселя (Томсона) (рис. 12.6).

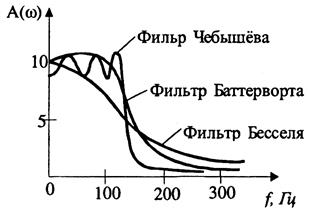
Рис. 12.6. Амплитудно-частотные характеристики фильтров

Фильтры Баттерворта характеризуются наиболее плоской амплитудно-частотной характеристикой в полосе пропускания. Это их достоинство. Но в переходной полосе указанные характеристики спадают плавно, недостаточно резко.

Фильтры Чебышева отличаются резким спадом амплитудно-частотных характеристик в переходной полосе, но в полосе пропускания эти характеристики не являются плоскими.

Фильтры Бесселя характеризуются очень пологим участками амплитудно-частотных характеристик в переходной полосе, еще более пологими, чем у фильтров Баттерворта. Их фазочастотные характеристики достаточно близки к идеальным, соответствующим постоянному времени замедления, поэтому такие фильтры мало искажают форму входного сигнала, содержащего несколько гармоник.