Краткие теоретические сведения. Рассмотрим процессы заряда и разрядки конденсатора при подключении или отключении источника постоянной ЭДС e0 в схеме

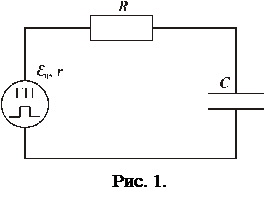Рассмотрим процессы заряда и разрядки конденсатора при подключении или отключении источника постоянной ЭДС e₀ в схеме, представленной на рис.1.

Включение и отключение ЭДС имитирует генератор прямоугольных импульсов напряжения. При включении ЭДС (появлении импульса) ток при заряде конденсатора протекает по внутреннему сопротивлению источника r и по сопротивлению резистора R.

Применяя к контуру второе правило Кирхгофа (в замкнутом контуре алгебраическая сумма ЭДС равна алгебраической сумме падений напряжений на всех сопротивлениях, входящих в этот контур), получим:

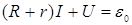. (1)

Здесь I – мгновенное значение силы тока, U – мгновенное значение напряжения на конденсаторе. Выразим их через заряд q на обкладках конденсатора, используя определения силы тока и емкости конденсатора C:

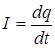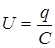; . (2)

Исключая в (1) величины I и U, используя соотношения (2) получим:

. (3)

При решении уравнения учтем, что в начальный момент времени 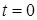, заряд на конденсаторе равен нулю: 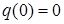. Решением дифференциального уравнения (3) является выражение:

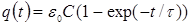, (4)

где 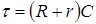– постоянная, имеющая размерность времени. Она называется постоянной времени RC-цепи. Выражение для величины U получим из связи между зарядом конденсатора и напряжением на его обкладках (2):

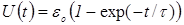. (5)

Временная зависимость напряжения на конденсаторе представлена на рис. 2.

Прологарифмируем выражение (5) и получим:

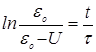(6)

Выражение (6) позволяет определить величину t как промежуток времени, по истечении которого напряжение на конденсаторе достигает величины 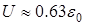, в этом случае 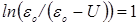(рис.2).

Таким образом, постоянная времени определяет скорость заряда конденсатора.

Зависимость величины t от сопротивления R линейная 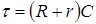, откуда величина емкости конденсатора:

(7)