Задача оптимального распределения капитальных вложений в предприятия

На развитие трёх предприятий выделено 5 млн. руб. Известны эффективности вложений в каждое предприятие, заданные значениями нелинейных функций 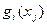, представленных в следующей таблице:

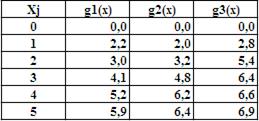
Графические представления функций показаны на Рис.1.

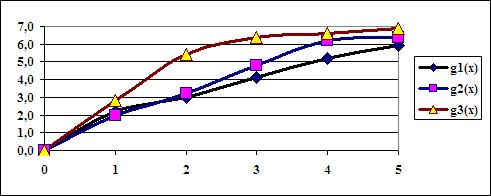
Рис.1. Графические представления функций эффективности.

Расчёты проведём в предположении, что распределение средств осуществляется в целых числах 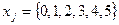млн. руб.

Поставленная задача может быть решена тремя способами:

· методом перебора;

· с помощью средства «Поиск решения»;

· методом динамического программирования.

Метод перебора. Применение данного метода оправдывается тем, задача решается в целых числах с малым диапазоном значений переменных. В данном случае три переменные x₁, x₂ и x₃ принимают одно из шести возможных значений: 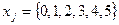. Следовательно, всего существует 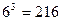комбинаций переменных. При этом из них для рассмотрения нужно отобрать только те, на которых .

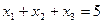Исходные данные занесены на рабочий лист приложения MS Excel, как показано на Рис.2.

Рис.2. Организация исходных данных на рабочем листе.

Для систематического перебора всех комбинаций рационально перевести десятичные числа в диапазоне от 0 до 215 в шестеричную систему счисления. Отдельные разряды шестеричного представления и будут значениями искомых переменных.

Возможный вариант перевода десятичных номеров комбинаций в разряды шестеричного кода представлен на Рис.3.

Рис.3. Формулы перевода десятичных номеров комбинаций в шестеричный код.

Расчёт эффективности вложений выполнен в столбце g1+g2+g3. Для этого в ячейку E14 введена формула:

=ЕСЛИ(B14+C14+D14=5;ПРОСМОТР(B14;$B$3:$B$8;$C$3:$C$8)+ПРОСМОТР(C14;$B$3:$B$8;$D$3:$D$8)+ПРОСМОТР(D14;$B$3:$B$8;$E$3:$E$8);0), которая затем распространена (протянута) до нижней части таблицы (Рис.4).

Рис.4. Формулы расчёта общей эффективности с учётом ограничений на переменные x1, x2 и x3.

Для выбора оптимального решения в ячейку F14 введена формула выбора максимального значения из всего диапазона вариантов, а ячейки G14, H14 и I14 введены формулы выбора из диапазона разрядов той комбинации x₁, x₂ и x₃, на которой достигается этот максимум (Рис.5).

Рис.5. Формулы выбора лучшего решения.

Для облегчения визуального поиска лучшего решения столбец с суммарной эффективностью рационально условно отформатировать на равенство максимальному значению суммарной эффективности. Фрагмент листа с отображением окончательного решения представлен на Рис.6.

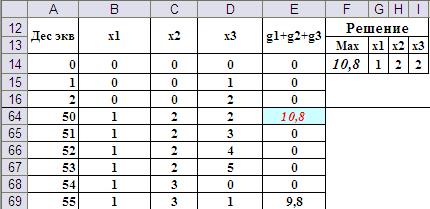
Рис.6. Окончательные результаты решения методом перебора.

«Поиск решения». Средство «Поиск решения» позволяет накладывать ограничения целочисленности переменных. Поэтому данная задача может быть решена этим средством.

На Рис.7 представлена возможная организация рабочего листа, а Рис.8 – настройка опций средства «Поиск решения».

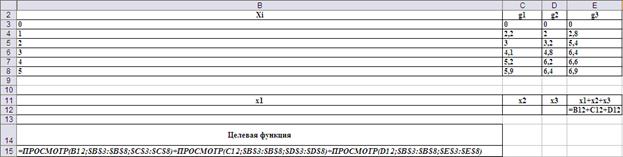
Рис.7. Организация рабочего листа при использовании средства «Поиск решения»

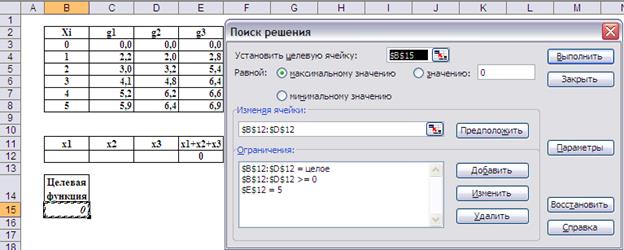
Рис.8. Настройка опций средства «Поиск решения»

Результаты решения (Рис.9) совпадают с результатами, полученными методом перебора.

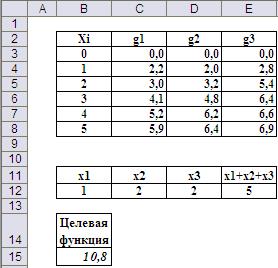
Рис.9. Окончательные результаты решения с помощью средства «Поиск решения»

Метод динамического программирования. Рассмотренные выше методы решения рационально применять при малых размерностях задачи. В случае большого количество предприятий и большой суммы инвестиций применяют метод динамического программирования.

В соответствии с идеей метода задача решается в два этапа.

1 этап. Условная оптимизация (k=3, 2, 1).

1-ый шаг: k=3. Он выполняется в предположении, что все средства в количестве x₃=5 млн. руб. отданы третьему предприятию. В этом случае максимальный доход, как видно из таблицы исходных данных и таблицы для функции Беллмана 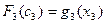составит 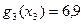млн. руб.

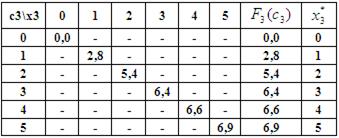
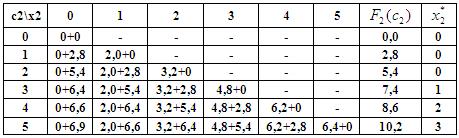
2-ой шаг: k=2. Определяем оптимальную стратегию при распределении денежных средств между вторым и третьим предприятиями. При этом рекуррентное соотношение Беллмана имеет вид:

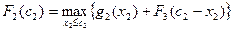
На основе последнего соотношения строится таблица для функции Беллмана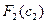

3-ой шаг: k=1. Определяем оптимальную стратегию при распределении денежных средств между первым и двумя другими предприятиями, используя формулу для расчёта суммарного дохода:

,

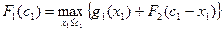на основе которого составлена таблица для функции Беллмана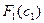

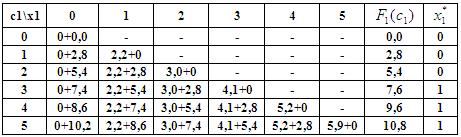
2 этап. Безусловная оптимизация (k=1, 2, 3).

Определяем траекторию оптимальной стратегии.

1-ый шаг: k=1. По данным таблицы для функции Беллмана 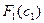оптимальный план при распределении 5 млн. руб. между тремя предприятиями составляет: 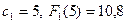. При этом первому предприятию нужно выделить 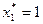млн. руб.

2-ой шаг: k=2. Определяем величину оставшихся денежных средств, приходящуюся на долю второго и третьего предприятий:

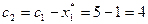млн. руб.

По данным таблицы для функции Беллмана 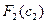находим, что оптимальный вариант распределения денежных средств размером 4 млн. руб. между вторым и третьим предприятиями составляет: 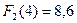при выделении второму предприятию 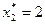млн. руб.

3-ий шаг: k=3. Определяем величину оставшихся денежных средств, приходящуюся на долю третьего предприятия:

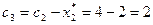млн. руб.

По данным таблицы для функции Беллмана 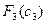находим:

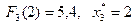млн. руб.

Траектория шагов второго этапа наглядно представлена на Рис.10.

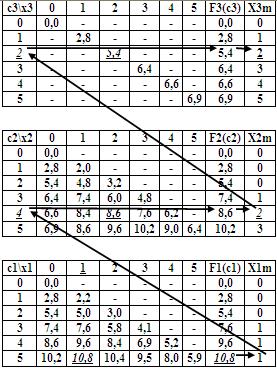
Рис.10. Траектория шагов второго этапа оптимизации методом динамического программирования

Таким образом, оптимальный план инвестирования предприятий: 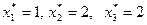, который обеспечивает максимальный доход, равный

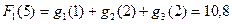млн. руб.

Итак, задача оптимального распределения инвестиций между тремя предприятиями решена тремя способами. Все они дали одинаковые результаты. Какому из них отдавать предпочтение при решении подобных задач? Рекомендации следующие. При малых размерностях проще решать методом перебора или с помощью средства «Поиск решения». Эти методы просты для понимания и для реализации. Однако при больших размерностях рационально использовать алгоритм динамического программирования. Он устойчив в решении и наиболее быстродействующий. Освоение метода требует определённых умственных усилий. Выше рассмотрено решение данным методом «вручную». Для решения подобных задач с другими исходными данными рационально автоматизировать процесс составления таблиц функций Беллмана.

На Рис.11 показан возможный вариант организации таблиц на листе приложения MS Excel.

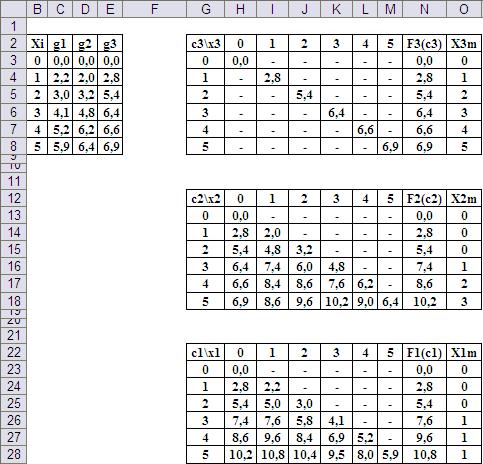
Рис.11. Организация данных на рабочем листе.

На Рис.12 показан фрагмент рабочего листа в режиме отображения формул. Ячейки H3, H13 и H23 соответствуют верхним левым углам таблиц функций Беллмана 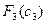, , 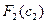, 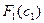соответственно. Адресация ячеек в формулах обеспечивает автоматическое заполнение всех таблиц при распространении формул по всему полю таблиц.

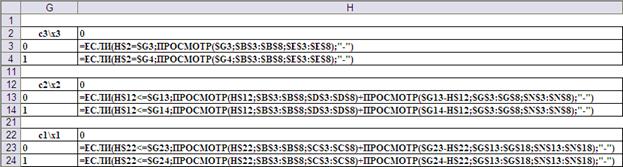
Рис.12. Ввод формул в ячейки рабочего листа для заполнения основных полей таблиц функций Беллмана

Вычисление максимальных значений функций и нахождение соответствующих значений аргументов осуществляется с помощью функций МАКС() и ПОИСКПОЗ() (Рис.13).

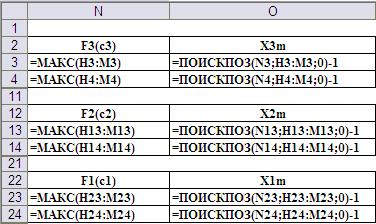
Рис.13. Ввод формул в ячейки рабочего листа нахождения максимальных значений функций и нахождения соответствующих аргументов.