Меры среднего
Мера среднего — это просто показательная точка на шкале, сжато отражающая особенность имеющихся данных. Обычно используются три меры среднего: среднее значение, медиана и мода.
Среднее значение (или просто среднее) — это знакомое нам арифметическое среднее, получающееся при сложении всех величин и делении полученной суммы на их количество. Сумма сырых величин из табл. П1 равна 1125. Если поделить ее на 15 (общее количество величин), то среднее будет 75.
Медиана — отметка среднего элемента последовательности, полученной путем расположения всех величин по порядку и затем отсчета к середине, начиная с любого конца. Если 15 величин из табл. П1 расположить по порядку от самого большого к самому малому 8-я величина с любого конца будет равна 75. Если исходное количество величин будет четным, то мы просто считаем среднее от тех двух, которые оказываются в середине.
Мода — это самый часто встречающийся показатель в данной выборке. Самая частая величина в табл. П1 — это 75, следовательно, мода этого распределения равна 75.
При нормальном распределении, когда величины распределены поровну с каждой стороны от середины (как на рис. П1), среднее, медиана и мода одинаковы. Это не так для скошенных, или несимметричных, распределений. Предположим, нам надо проанализировать времена отправления утреннего поезда. Обычно поезд отправляется вовремя; случается, он отправляется позже, но он никогда не уходит раньше времени. У поезда с отправлением по расписанию в 08:00 время отправления в течение недели может оказаться таким:
Пн: 08:00
Вт: 08:04
Ср: 08:02
Чт: 08:19
Пт: 08:22
Сб: 08:00
Вс: 08:00
Это распределение времен отправления является скошенным из-за двух запоздавших отправлений; они увеличивают среднее время отправления, но не сильно влияют на медиану и моду.
Важно понять смысл скошенного распределения, поскольку иначе разницу между медианой и средним иногда трудно уловить (рис. П2). Если, например, руководство фирмы и ее профсоюз спорят из-за благосостояния работников, средняя величина расходов на зарплату и их медиана могут сдвинуться в противоположных направлениях. Предположим, фирма поднимает зарплату большинству сотрудников, но урезает зарплату высшим управленцам, которые были слишком высоко на шкале оплаты; тогда медиана зарплаты может подняться вверх, тогда как средняя величина зарплаты снизится. Сторона, стремящаяся показать, что зарплата возросла, выберет в качестве индикатора медиану, а сторона, стремящаяся показать снижение зарплаты, выберет среднее.
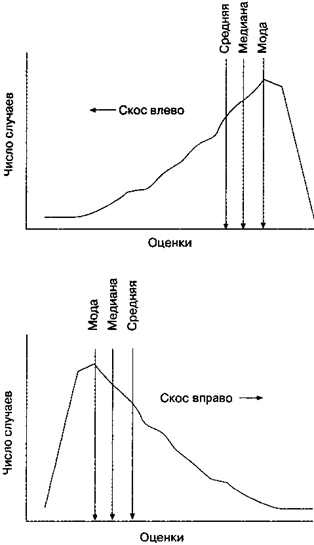
Рис. П2. Кривая скошенного распределения.Заметьте, что скос распределения имеет то направление, в котором спадает его хвост. Заметьте также, что у скошенного распределения среднее, медиана и мода не совпадают; медиана обычно находится между модой и средним.
Дата добавления: 2015-02-19; просмотров: 952;
