Независимые события.

Два события A и B называются независимыми, если P(A/B)=P(A); P(B)=P(B/A) - доказать.

В этом случае вероятность наступления двух событий A и B равна P(AB)=P(B)P(A/B)=P(A)P(B),

при этом покажем, что P(B/A)=P(B); P(AB)=P(B)P(A)=P(A)P(B/A)

События A₁A₂...A_k называются независимыми между собой, если вероятность их совместного наступления 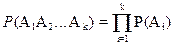; 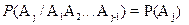. Два независимых события совместны.

* Если бы события были несовместны, то P(A/B)=0 и P(B/A)=0, т.к. они независимы, то P(A/B)=P(A) и P(B/A)=P(B), т.е. утверждение “независимые события несовместны”, т.к. P(A)=0 и P(B)=0, то это утверждение неверно.