Индуктивность

Мгновенные значения тока и напряжения для индуктивности связаны между собой следующими соотношениями:

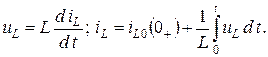
Применяя к этим выражениям теоремы дифференцирования и интегрирования, получаем компонентные уравнения индуктивности в операторной форме:

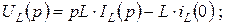
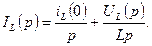
При нулевых начальных условиях эти уравнения примут вид

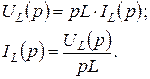
Используя эти выражения, определяем операторное входное сопротивление и операторную входную проводимость индуктивности:

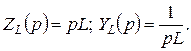
Операторным компонентным уравнениям при ненулевых начальных условиях соответствуют последовательная и параллельная схемы замещения индуктивности, содержащие независимый источник тока или напряжения (рис. 6.19 а, б).

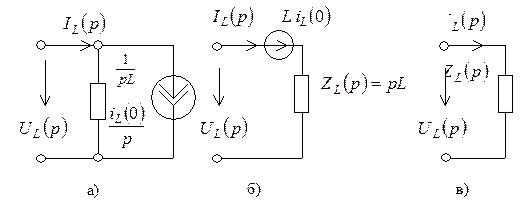
Рис. 6.19. Операторные схемы замещения индуктивности:

а – параллельная при ненулевых начальных условиях; б – последовательная при ненулевых начальных условиях; в – при нулевых начальных условиях

Используя операторные схемы замещения идеализированных пассивных элементов, можно получить операторную схему замещения произвольного участка линейной цепи или всей цепи в целом. С этой целью каждый идеализированный пассивный элемент должен быть заменен операторной схемой замещения, а токи и напряжения идеализированных источников тока и напряжения — представлены соответствующими операторными изображениями.

Используя операторную схему замещения цепи, можно с помощью любого из известных методов сформировать систему уравнений электрического равновесия в операторной форме, которая будет равносильна основной системе уравнений электрического равновесия цепи после коммутации.

Метод анализа переходных процессов в линейных цепях, основанный на формировании операторных уравнений электрического равновесия цепей по их операторным схемам замещения, получил название операторного метода анализа переходных процессов.