Включение RLC-цепи на постоянное напряжение
Рассмотрим переходный процесс в цепи второго порядка на примере простейшей цепи (рис.6.3).
 Рис.6.3
Рис.6.3
Если цепь содержит хотя бы один емкостный элемент, то составленные дифференциальные уравнения решаются относительно напряжения на этом элементе.
Начальные условия нулевые: 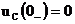 ,
, 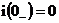 .
.
Принужденные составляющие: ucпр = U0 , iпр = 0.
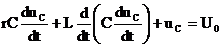 ;
;
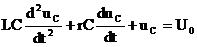 .
.
Видим, что составленное дифференциальное уравнение второго порядка.
Его характеристическое уравнение:
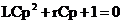 ,
,
или
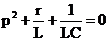 .
.
Тогда корни характеристического уравнения равны: 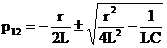 .
.
Но можно дифференциальное уравнение и не составлять, а воспользоваться тем же приемом, что и для цепей первого порядка, то есть воспользоваться условием: Z(p)=0 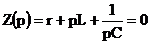
или после преобразований: 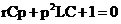 .
.
Откуда видно, что характеристическое уравнение, полученное из условия Z(p) = 0, имеет тот же вид, что и характеристическое уравнение, полученное из дифференциального.
Дальнейшее решение можно проделать по одному из трех вариантов.
1)Если обозначить 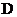 =
= 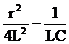 , то при D > 0:
, то при D > 0:
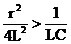 ,
,
где 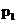 и р2 – действительные числа и они меньше нуля.
и р2 – действительные числа и они меньше нуля.
Тогда решение для напряжения находят в виде:
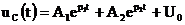 .
.

Рис. 6.4 Рис. 6.5
В этом решении две неизвестные постоянные интегрирования А1 и А2, поэтому нужно вспомогательное уравнение для определения 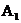 и
и 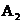 . Пусть это будет ток:
. Пусть это будет ток:
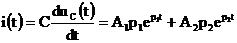 .
.
При 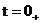 решения для тока и напряжения при
решения для тока и напряжения при  мут вид:
мут вид:
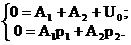
Из второго уравнения получаем:
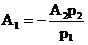 .
.
Подставим найденное значение А1 в первое уравнение, получим: Рис. 6.6
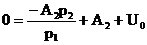 ,
,
отсюда
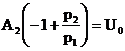 или
или 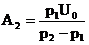 .
.
Тогда: 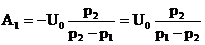 .
.
Напряжение на индуктивности можно найти по формуле:
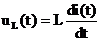 .
.
Построим возможные временные графики переходных процессов. Для случая D > 0 приведены временные графики: uc(t) – на рис. 6.4, i(t) – на рис. 6.5, uL(t) – на рис. 6 .6.
2) Если D < 0, то 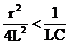 . Тогда корни характеристического уравнения
. Тогда корни характеристического уравнения 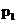 и
и 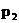 будут комплексные. Представим их в виде:
будут комплексные. Представим их в виде:
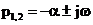 ,
,
где 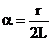 ,
, 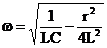 .
.

Рис. 6.7 Рис. 6.8
В этом случае решение следует искать в виде:
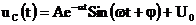 ;
;
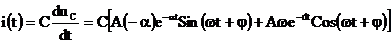 .
.
Из начальных условий, при 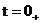 определяем А и
определяем А и 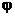 . Для этого составляем и решаем уравнения:
. Для этого составляем и решаем уравнения:
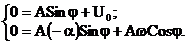
Покажем, что здесь также можно использовать решение из первого случая:
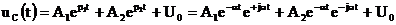 .
.
Рассмотрим только свободную составляющую:

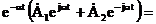
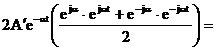
= 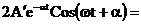
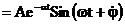 , Рис. 6.9
, Рис. 6.9
где 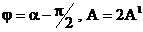 .
.
Построим возможные временные графики переходных процессов. Для случая D < 0 временные графики приведены: uc(t) – на рис. 6.7, i(t) – на рис. 6.8 uL(t) – на рис. 6.9.
3) Если D = 0, то 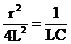 , и корни будут одинаковыми:
, и корни будут одинаковыми:
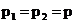 .
.

Рис.6.10 Рис. 6.11
Решение следует искать в виде:
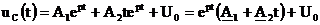 ;
;

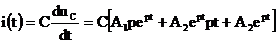
Из начальных условий, при 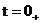 определяем А1 и А2:
определяем А1 и А2:
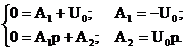
Построим возможные временные графики переходных процессов. Для случая D = 0
|
i(t) – на рис. 6.11, uL(t) – на рис. 6.12.
Дата добавления: 2015-02-16; просмотров: 1551;
