Элементы электрических цепей

Пассивные элементы электрической цепи

В основе теории электрических цепей лежит принцип моделирования. При этом реальные электрические цепи заменяются некоторой идеализированной моделью, состоящей из взаимосвязанных идеализированных элементов. Последние представляют собой простые модели, используемые для аппроксимации (приближения) свойств простых физических элементов или физических явлений. В зависимости от точности приближения одна и та же физическая электрическая цепь может быть представлена различными моделями, причем, чем точнее модель, тем она сложнее. На практике обычно ограничиваются наиболее простыми моделями, обеспечивающими решение задач анализа и синтеза реальной цепи с заданной точностью.

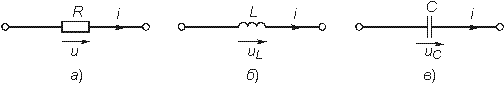
Рис. 1.2

К простейшим идеализированным элементам модели электрической цепи относятся независимые и зависимые источники (активные элементы, см. далее) и элементы резистивного сопротивления, индуктивности и емкости (пассивные элементы). Связь между током и напряжением на этих элементах называют компонентными уравнениями.

Пассивные элементы. Резистивным сопротивлением называют идеализированный элемент, обладающий только свойством необратимого рассеивания энергии. Условное обозначение резистивного сопротивления показано на рис. 1.2, а. Математическая модель, описывающая свойства резистивного сопротивления, определяется законом Ома (компонентное уравнение):

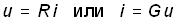. (1.1)

Коэффициенты пропорциональности R и G в формулах (1.1) называются соответственно сопротивлением и проводимостью элемента и являются его количественной характеристикой, причем при согласованных направлениях тока и напряжения R и G положительны и связаны обратной зависимостью R=1/G. Измеряют в системе СИ сопротивление R в омах (Ом), а проводимость G – в сименсах (См).

Уравнение (1.1) определяет зависимость напряжения от тока и носит название вольт-амперной характеристики (ВАХ) резистивного сопротивления. Если R постоянно, то ВАХ линейна (рис. 1.3, а) и соответствует линейному резистивному элементу. Если же R зависит от протекающего через него тока или приложенного к нему напряжения, то ВАХ становится нелинейной (рис. 1.3, б) и соответствует нелинейному резистивному сопротивлению.

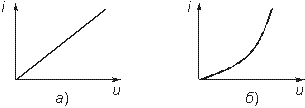
Рис. 1.3

Мощность в резистивном сопротивлении можно определитьпутем умножения мгновенных значений тока и напряжения:

.

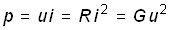Мощность в резистивном сопротивлении всегда больше нуля, так как оно только потребляет энергию, преобразуя ее в тепло или другие виды энергии.

Индуктивным элементом называют идеализированный элемент электрической цепи, обладающий только свойством накопления им энергии магнитного поля. Условное обозначение индуктивного элемента изображено на рис. 1.2, б.

Математическая модель, описывающая свойства индуктивного элемента определяется соотношением

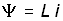, 1.2

где 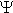– потокосцепление, характеризующее суммарный магнитный поток, пронизывающий катушку:

,

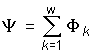где w – число витков катушки; k – номер витка, с которым сцеплен поток Ф _k. В простейшем случае, когда каждый из потоков Ф _k сцеплен со всеми витками катушки 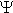=Ф w.

Коэффициент пропорциональности L в формуле (1.2) называется индуктивностью. Он имеет положительное значение и является количественной стикой индуктивного элемента. Измеряется индуктивность L в генри (Гн), а магнитный поток Ф – в веберах (Вб). Если величина L постоянна, то зависимость (1.2) (вебер-амперная характеристика) линейна и соответствует линейному индуктивному элементу.Если же L зависит от электрического режима (тока или напряжения), то зависимость (1.2) нелинейна и соответствует нелинейному элементу индуктивности.

Связь между током и напряжением на индуктивном элементе определяется согласно закону электромагнитной индукции выражением (компонентное уравнение)

,

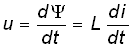т. е. напряжение на индуктивном элементе пропорционально скорости изменения протекающего через него тока. Следовательно, при протекании через L постоянного тока и=0 и свойства индуктивного элемента эквивалентны коротко замкнутому (КЗ) участку (см. рис. 1.1, а).

Мгновенная мощность электрических колебаний в индуктивном элементе

,

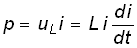т. е. может быть как положительной (при совпадении направлений и и i), так и отрицательной (при несовпадении направлений ииi). Причем в первом случае (p>0) магнитная энергия запасается индуктивным элементом, а во втором (р<0) – отдается во внешнюю цепь.

Энергия, запасенная в индуктивном элементе к моментуt, определится согласно

,

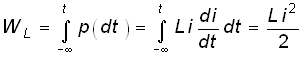т. е. всегда положительна.

Емкостным элементом называют идеализированныйэлементэлектрической цепи, обладающий только свойством накапливать энергию электрического поля. Условное обозначение емкостного элемента показано на рис. 1.2, в.

Математическая модель, описывающая свойства емкостного элемента, определяется вольт-кулонной характеристикой

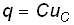. 1.3

Коэффициент пропорциональности С в формуле(1.3) называется емкостью и является количественной характеристикой емкостного элемента. При согласованных направлениях тока и напряжения величина С всегда положительна. Измеряется С в фарадах (Ф).

Если величина С постоянная, то вольт-кулонная характеристика (1.3) линейна и соответствует линейному емкостному элементу. Если же параметр С зависит от электрического режима, то характеристика (1.3) нелинейна и соответствует нелинейномуэлементу.

Между током и напряжением на емкостном элементе существует связь, определяемая равенством (компонентное уравнение)

,

т. е. ток в емкостном элементе пропорционален скорости изменения приложенного к нему напряжения. При постоянном напряжении u=const, i=0 и емкостной элемент по своим свойствам эквивалентен разрыву цепи.

Мощность электрических колебаний в емкостном элементе

,

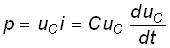т. е. может быть как положительной, так и отрицательной в зависимости от направлений тока и напряжения. При р>0 энергия электрического поля запасается емкостным элементом, а при р<0 – отдается во внешнюю цепь.

Энергия, запасенная в емкостном элементе к моменту t,

,

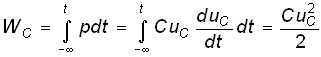т. е. всегда положительна.

В инженерной практике резистивное сопротивление, индуктивный и емкостной элементы часто называют просто сопротивлением, индуктивностью и емкостью, отождествляя, по существу, элемент с его параметром. В дальнейшем для простоты, где это не приведет к недоразумениям, также будем пользоваться этой терминологией.

Рассмотренные идеализированные резистивный, индуктивный и емкостной элементы могут служить простейшими моделями резисторов, высококачественных катушек индуктивностей с малыми потерями и электрических конденсаторов с высокими диэлектрическими свойствами в области низких и средних частот. В области высоких, а особенно сверхвысоких частот модели резисторов, катушек индуктивности и конденсаторов становятся более сложными. Так, на высоких частотах резисторы уже нельзя с достаточной точностью описать идеальным резистивным элементом из-за влияния различных “паразитных” емкостей, а так же индуктивностей.