Методы пересчета к. п. д. с модели на натуру.

Исключительно важным в гидротурбостроении является точное определение к. п. д. при выдаче гарантий по результатам испытаний модели (обычно меньшей по размерам в 10 и более раз). Однако пересчет к. п. д. с модели на натуру представляет значительные трудности как теоретического, так и практического характера и ведется приближенными методами. Существует большое число формул и методов пересчета. Их можно подразделить на две большие группы.

Первая группа формул основана на том, что все гидравлические потери в турбине считаются подчиненными влиянию вязкого трения и могут быть пересчитаны на основании критерия подобия Рейнольдса в зависимости от масштаба. Но при этом предполагают, что потери в гидротурбине зависят от размеров так же, как в круглых трубопроводах. Тогда, используя формулу Дарси, можно выразить потери через:

Δh_ТР = λ·(l / d)·(v²/ 2g)

где λ — коэффициент гидравлического трения при турбулентном течении; l — длина; d — диаметр; v — скорость течения в трубопроводе. Путем некоторых преобразований и замен из выражения (VI.62) можно получить в общем виде отношение потерь в турбине и модели:

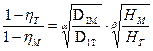
где η_ГТ и η_ГМ, D_1Т и D_2М, Н_Т и Н_М — соответственно гидравлические к. п. д., диаметры рабочего колеса и напоры натуры и модели (отношение напоров рекомендуется учитывать при Н ≥ 60 м.)

Эта формула в зависимости от применяемых в ней показателей корней известна под именами разных авторов. Из таких модификаций широкое распространение имела раньше формула Мууди, носящая имя американского инженера, рекомендовавшего ее еще в 20-х годах XX века в виде:

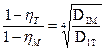
Однако при λ = D_1Т / D_1М ≥ 10 поправки по этой формуле получаются слишком большими. Кроме того, в таком виде эта формула не учитывает влияния напора. Для уменьшения погрешностей при больших λ Г. Ф. Проскура рекомендовал принять в данном выражении значение степени корня ά = 5.

Эта формула вполне пригодна для предварительных оценок к. п. д. при масштабах λ =10 ÷ 20 и повышенных напорах, которые имеет смысл учитывать при Н > 60 ÷ 100 м.

Обладая простотой формы, корневые формулы являются во всех вариантах весьма приближенными и в последнее время для более точных расчетов не применяются.

Отыскание более точных формул стало особенно важным после того, как в международной практике утвердился метод выдачи окончательных гарантий по к. п. д. на основании модельных испытаний, проводимых на достаточно точных, эталонных, стендах. Широкое применение эта практика нашла потому, что натурные испытания, производившиеся для проверки гарантий по к. п. д., себя не оправдали, так как их погрешность получается порядка ±2%, что превышает требуемую точность порядка ±0,5%.

Поэтому в настоящее время гарантии часто предусматривают специальные методы пересчета, в которых только часть потерь считается зависимой от масштабного эффекта.

Формулы пересчета этого типа составляют вторую группу и в общем виде могут быть представлены в общем выражении как:

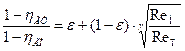
где ε — доля непересчитываемых потерь.

Эти формулы свободны от логически неправильного предположения, по которому все потери считались зависящими от вязкого трения, а течение в гидротурбинах принималось подобным течению в круглых трубах. Однако главную трудность в них представляет определение доли непересчитываемых потерь ε.

Исследованиями, проведенными в ЦКТИ им. Ползунова, в КБ «ЛМЗ» и в ряде зарубежных лабораторий, установлен ряд гидравлических потерь, не зависящих или мало зависящих от масштабного эффекта, и рекомендованы конкретные значения έ. Рекомендуется ε = 0,25 и γ = 5, что дает формулу пересчета:

η_ГТ = 1-(1-η_ГМ)[ε + (1- ε)·⁵√Re_М / Re_Т] или

η_ГТ = 1-(1-η_ГМ)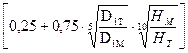

При практических расчетах определяется поправка по η в оптимальном режиме Δ η = η_ГТ – η_ГМ ≈ (1,5 ÷ 3,5)%, которая принимается для всего диапазона работы гидротурбины.

Рассматривая этот вопрос схематически, к основным непересчитываемым потерям можно отнести:

· потери на удар в рабочем колесе и на перетекание на концах лопастей;

· вихревые потери;

· потери, связанные с наличием циркуляции в отсасывающей трубе;

· потери на выходе из отсасывающей трубы с выходной скоростью, в большой мере зависящие от неравномерности потока, определяемой коэффициентом Кориолиса α;

· и некоторые другие.

Частично и, по-видимому, в малой степени зависят от масштабного эффекта потери в колене отсасывающей трубы. От относительной шероховатости зависят характер обтекания и потери на трение о стенки проточных элементов турбины и отсасывающей трубы. Обычно принято считать, что течение в турбине является гидродинамически более гладким, чем в модели, а относительная шероховатость — меньшей, а поэтому связанные с ней потери тоже меньшими. Однако исследования течения в тщательно выполненных моделях, по некоторым данным, показывали и обратный результат. Это подтверждает, что оценку влияния шероховатости надо производить особо в каждом конкретном случае, оценивая неровности в модели и турбине. К столь же трудным сопоставлениям, зависящим от исполнения, приводит оценка объемных потерь через зазоры в радиально-осевых турбинах и механических потерь в модели и натуре. Поэтому в общем виде доля непересчитываемых потерь трудно поддается определению расчетом и в значительной мере обосновывается опытными данными.