Применение теории подобия в гидротурбинах.
1. Геометрическое подобие. Для модели должно быть выполнено полное геометрическое подобие проточных частей, т. е. внутренних очертаний спиральной камеры, направляющего аппарата, рабочего колеса, отсасывающей трубы. Линейные масштабные коэффициенты при этом ограничиваются минимальными размерами моделей, для которых в настоящее время применяют рабочие колеса диаметром D1 МОД = 250 мм или D1 МОД = 460 мм Конструктивные элементы механизмов, наружные очертания, подшипники, вал и др., их жесткость не моделируются или моделируются приближенно. Не удается моделировать полностью зазоры в проточном тракте и шероховатости.
Условия механического подобия модели и натуры в гидротурбинах принимаются аналогичными общим условиям подобия, т. е. включают в себя следующее:
2. Кинематическое подобие. Полное кинематическое подобие, под которым понимается, что векторы скорости в потоке подобны, или компланарны, т. е. направлены одинаково и по величине пропорциональны напорам:
vi = ki • 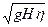
где ki –скоростной коэффициент.
 |
Будем считать, что из условия подобия турбины и модели треугольники скоростей в них в соответствующих точках также подобны, а скоростные коэффициенты при одинаковых режимах — одинаковы.
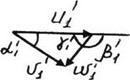 |
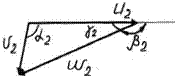 |
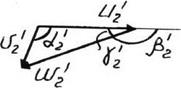 |
Рисунок 7.1 Треугольники скоростей на входе и выходе рабочего колеса при изогональных режимах (индексами обозначены скорости в модели)
Для доказательства воспользуемся основным уравнением турбины:
ηГgH = u1v1cosά1 – u2v2cosά2
в котором левая часть основного уравнения турбин ηГgH – энергия в Дж полученная рабочим колесом от объема жидкости весом в 1Н, прошедшей через лопастную систему рабочего колеса. Правая часть уравнения – кинематические параметры потока при входе на рабочее колесо и после выхода из него.
Из треугольника скоростей на входе (рисунок 7.2), на основании теоремы косинусов, имеем:
w21 = u21 + v21 – 2u1v1cosά1
w22 = u22 + v22 – 2u2v2cosά2
Заменяя в уравнении турбины величины u1v1cosά1 и u2v2cosά2 соответствующими значениями скоростей, получим:
ηГH = 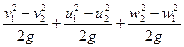
и для нормального выхода, когда ά2 ≈ 90º, cos ά2 = 0 а значит Г2 = 0, имеем:
ηГH = 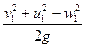 , или 2gηГH= v21 + u21 - w21
, или 2gηГH= v21 + u21 - w21
Для определения скоростных коэффициентов ki, найдем зависимость скоростей абсолютной v1 окружной u1 и относительной w1от рабочего напора H, гидравлического к. п. д. ηГ и углов ά1 β1иγ1 и ά2 β2иγ2 треугольников скоростей на входе в рабочее колесо и выходе из него. Для упрощения задачи будем предполагать, что выход воды из рабочего колеса нормальный.
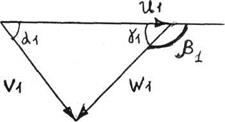
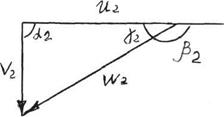
а) б)
Рисунок 7.2 Треугольник скоростей на входе а) и на выходе б) из турбины
Используем основное уравнение теории турбин в следующем виде:
ηГgH = u1v1cosά1
Из треугольника скоростей на входе (рисунок 7.2), на основании теоремы синусов имеем:
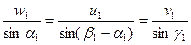
Отсюда
v1 = 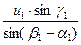
w1 = 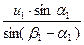
Подставляя в уравнение турбины для нормального выхода вместо v1 ее значение получим:
2gηГH = 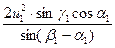
откуда
u1 = 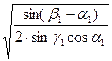
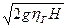 = КU •
= КU • 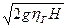
соответственно решая относительно v1 и w1 получим:
v1 = 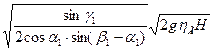 =КV •
=КV • 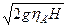
w1 = 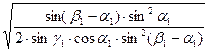
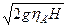 =КW •
=КW • 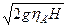
Таким образом, эти выражения устанавливают зависимости v1, u1 и w1 от Н,ηГ, ά1, β1. Из этих выражений видно, что скоростные коэффициенты определяются только углами ά1, ά2 и β1, β2, которые в подобных турбинах при одинаковых режимах являются однозначными и зависят только от положения лопаток направляющего аппарата и лопастей рабочего колеса. Такие режимы обычно называют изогональными. Очевидно, что каждому режиму работы турбины при заданном напоре соответствует свой изогональный режим.
Изогональные режимы зависят: в радиально-осевых и пропеллерных гидротурбинах только от углов ά1, ά2, величины которых определяются положением (открытием) лопаток направляющего аппарата; в поворотно-лопастных гидротурбинах как от углов ά1, ά2, зависящих от положения лопаток направляющего аппарата, так и от углов β1, β2, которые определяются углом поворота лопастей рабочего колеса φ.
Очевидно, что подобие изогональных режимов, определяемое только подобием планов скоростей, и не зависит от их величины, а следовательно, и от отношения напоров. Отсюда следует важный вывод: подобные турбины остаются подобными, работая при различных напорах.
Условия кинематического подобия, включающие условия геометрического подобия, являются необходимыми, но недостаточными для полного механического подобия.
3. Динамическое подобие. Динамическое подобие, под которым понимается подобие потоков и действующих в них сил. Как следует из 7.1.3, эти условия требуют соблюдения критериев Рейнольдса, Фруда, Струхаля и Эйлера, что при наличии вязкой жидкости в турбинах не выполнимо. Поэтому условия динамического подобия при изогональных режимах выполняются лишь частично.
Число Рейнольдса, характеризующее влияние сил вязкого трения в гидротурбинах, обычно выражают, заменяя характерный размер через диаметр рабочего колеса D1, а скорость v – через напор √Н, при g=const. Тогда:
Re = vl / ν → Re=√Н• D1 / ν
Критерий Рейнольдса в реактивных турбинах, где вязкое трение в большой мере определяет характер течения, следует принять – основным критерием динамического подобия.
Однако выполнение этого требования приводит при одинаковой вязкости воды в турбине и модели к тому, что согласно:
√НТ /√НМ = D1 Т / D1 М = λ
где λ –величина шероховатости поверхностей трения.
Диаметры должны быть обратно пропорциональны квадратным корням из напоров. Нетрудно видеть, что это практически невыполнимо, так как при λ =10 ÷ 20, как это обычно применяется, испытания модели пришлось бы производить при НМ = (100 ÷ 200)HТ, т. е. в сотни раз большем, чем в натуре.
Если при одинаковых напорах применять в натуре и модели жидкости разной вязкости, то из того же уравнения следует, что:
D1 Т / νТ = D1 М / νМ,то νМ = (D1 М / D1 Т)• νТ = 1 / λ
или вязкость в модельной установке должна быть меньше, чем вязкость воды, во столько раз, во сколько модель меньше турбины, т. е. в 10 – 20 раз. Такие жидкости для практического применения найти не удастся.
Несоблюдение критерия Рейнольдса при испытании моделей приводит к тому, что потери в них оказываются больше, чем в натурных, больших по размерам турбинах. Это несоответствие известно под названием масштабного эффекта и требует внесения поправок при пересчете данных с модели на натуру.
Опытами установлено, что при течении воды в круглых трубах при числах Re > 5•105 ÷ 106 потери практически не зависят от их размеров, и влиянием масштабного эффекта можно пренебречь. По аналогии эти результаты часто переносят на гидротурбины, стремясь к тому, чтобы испытания проводились при Re > 5•105 в так называемой области «автомодельности». Опыт показывает, что и в этих условиях влияние масштаба остается существенным и требует внесения поправок. Точных данных о влиянии масштабного эффекта на потери в гидротурбинах нет.
Дата добавления: 2015-02-16; просмотров: 1830;
