Нелинейные модели парной регрессии и корреляции
Различают два класса нелинейных регрессий:
1. Регрессии, нелинейные относительно включенных в анализ объясняющих переменных, но линейные по оцениваемым параметрам, например
· полиномы различных степеней – 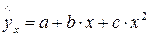 ,
, 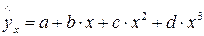 ;
;
· равносторонняя гипербола – 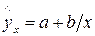 ;
;
· полулогарифмическая функция –  .
.
2. Регрессии, нелинейные по оцениваемым параметрам, например
· степенная – 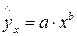 ;
;
· показательная – 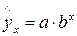 ;
;
· экспоненциальная – 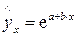 .
.
Регрессии нелинейные по включенным переменным приводятся к линейному виду простой заменой переменных (линеаризация), а дальнейшая оценка параметров производится с помощью метода наименьших квадратов. Рассмотрим некоторые функции.
Парабола второй степени 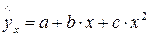 приводится к линейному виду с помощью замены:
приводится к линейному виду с помощью замены: 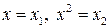 . В результате приходим к двухфакторному уравнению
. В результате приходим к двухфакторному уравнению  , оценка параметров которого при помощи МНК, приводит к системе следующих нормальных уравнений:
, оценка параметров которого при помощи МНК, приводит к системе следующих нормальных уравнений:
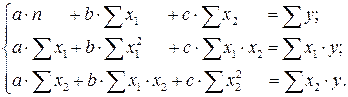
А после обратной замены переменных получим
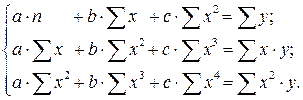 (1.17)
(1.17)
Парабола второй степени обычно применяется в случаях, когда для определенного интервала значений фактора меняется характер связи рассматриваемых признаков: прямая связь меняется на обратную или обратная на прямую.
Равносторонняя гипербола 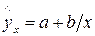 приводится к линейному уравнению простой заменой:
приводится к линейному уравнению простой заменой:  . Система линейных уравнений при применении МНК будет выглядеть следующим образом:
. Система линейных уравнений при применении МНК будет выглядеть следующим образом:
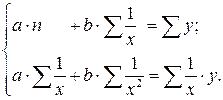 (1.18)
(1.18)
Аналогичным образом приводятся к линейному виду зависимости  ,
, 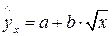 и другие.
и другие.
Несколько иначе обстоит дело с регрессиями нелинейными по оцениваемым параметрам, которые делятся на два типа: нелинейные модели внутренне линейные (приводятся к линейному виду с помощью соответствующих преобразований, например, логарифмированием) и нелинейные модели внутренне нелинейные (к линейному виду не приводятся).
К внутренне линейным моделям относятся, например, степенная функция – 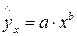 , показательная –
, показательная – 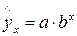 , экспоненциальная –
, экспоненциальная – 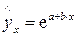 , логистическая –
, логистическая – 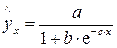 , обратная –
, обратная – 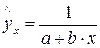 .
.
К внутренне нелинейным моделям можно, например, отнести следующие модели: 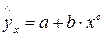 ,
,  .
.
Среди нелинейных моделей наиболее часто используется степенная функция 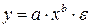 , которая приводится к линейному виду логарифмированием:
, которая приводится к линейному виду логарифмированием:
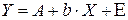 ,
,
где 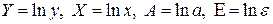 . Т.е. МНК мы применяем для преобразованных данных:
. Т.е. МНК мы применяем для преобразованных данных:

а затем потенцированием находим искомое уравнение.
Широкое использование степенной функции связано с тем, что параметр 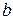 в ней имеет четкое экономическое истолкование – он является коэффициентом эластичности.
в ней имеет четкое экономическое истолкование – он является коэффициентом эластичности.
Коэффициент эластичности показывает, на сколько процентов измениться в среднем результат, если фактор изменится на 1%. Формула для расчета коэффициента эластичности имеет вид:
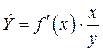 . (1.19)
. (1.19)
Так как для остальных функций коэффициент эластичности не является постоянной величиной, а зависит от соответствующего значения фактора 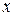 , то обычно рассчитывается средний коэффициент эластичности:
, то обычно рассчитывается средний коэффициент эластичности:
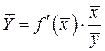 . (1.20)
. (1.20)
Приведем формулы для расчета средних коэффициентов эластичности для наиболее часто используемых типов уравнений регрессии:
Таблица 1.5
Вид функции, 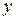
| Первая производная, 
| Средний коэффициент эластичности, 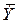
| Линеаризация |

| 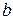
| 
| - |
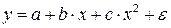
| 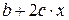
| 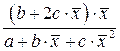
| Х1=х, Х2=х2 |

| 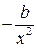
| 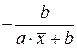
| Х=1/х,Y=y |
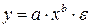
| 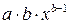
| 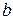
| Х=lnх,Y=lny |

| 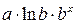
| 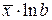
| Х=х,Y=lny |
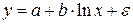
| 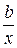
| 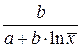
| Х=lnх,Y=y |
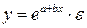
| 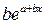
| 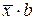
| Х=х,Y=lny |
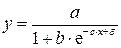
| 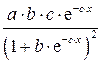
| 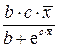
| |
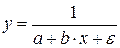
| 
| 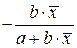
| Х=х,Y=1/y |
Уравнение нелинейной регрессии, так же, как и в случае линейной зависимости, дополняется показателем тесноты связи. В данном случае это индекс корреляции:
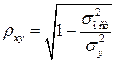 . (1.21)
. (1.21)
Величина данного показателя находится в пределах:  . Чем ближе значение индекса корреляции к единице, тем теснее связь рассматриваемых признаков, тем более надежно уравнение регрессии.
. Чем ближе значение индекса корреляции к единице, тем теснее связь рассматриваемых признаков, тем более надежно уравнение регрессии.
Квадрат индекса корреляции носит название индекса детерминации и характеризует долю дисперсии результативного признака 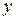 , объясняемую регрессией, в общей дисперсии результативного признака:
, объясняемую регрессией, в общей дисперсии результативного признака:
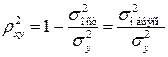 , (1.22)
, (1.22)
т.е. имеет тот же смысл, что и в линейной регрессии;
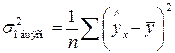 .
.
Индекс детерминации 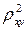 можно сравнивать с коэффициентом детерминации
можно сравнивать с коэффициентом детерминации 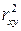 для обоснования возможности применения линейной функции. Чем больше кривизна линии регрессии, тем величина
для обоснования возможности применения линейной функции. Чем больше кривизна линии регрессии, тем величина 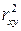 меньше
меньше 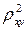 . А близость этих показателей указывает на то, что нет необходимости усложнять форму уравнения регрессии и можно использовать линейную функцию.
. А близость этих показателей указывает на то, что нет необходимости усложнять форму уравнения регрессии и можно использовать линейную функцию.
Индекс детерминации используется для проверки существенности в целом уравнения регрессии по  -критерию Фишера:
-критерию Фишера:
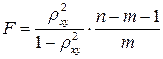 , (1.23)
, (1.23)
где 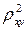 – индекс детерминации,
– индекс детерминации,  – число наблюдений,
– число наблюдений, 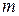 – число параметров при переменной
– число параметров при переменной 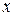 . Фактическое значение
. Фактическое значение  -критерия (1.23) сравнивается с табличным при уровне значимости
-критерия (1.23) сравнивается с табличным при уровне значимости 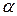 и числе степеней свободы
и числе степеней свободы 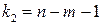 (для остаточной суммы квадратов) и
(для остаточной суммы квадратов) и 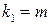 (для факторной суммы квадратов).
(для факторной суммы квадратов).
О качестве нелинейного уравнения регрессии можно также судить и по средней ошибке аппроксимации, которая, так же как и в линейном случае, вычисляется по формуле (1.8).
2. Множественная регрессия и корреляция
Парная регрессия может дать хороший результат при моделировании, если влиянием других факторов, воздействующих на объект исследования, можно пренебречь. Если же этим влиянием пренебречь нельзя, то в этом случае следует попытаться выявить влияние других факторов, введя их в модель, т.е. построить уравнение множественной регрессии
 ,
,
где 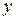 – зависимая переменная (результативный признак),
– зависимая переменная (результативный признак), 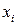 – независимые, или объясняющие, переменные (признаки-факторы).
– независимые, или объясняющие, переменные (признаки-факторы).
Дата добавления: 2015-02-16; просмотров: 1162;
