Модель взаимосвязи риска и доходности
Любое предприятие может рассматриваться как совокупность некоторых активов (материальных и финансовых), находящихся в определенном сочетании. Владение любым из этих активов связано с определенным риском в плане воздействия этого актива на величину общего дохода предприятия. То же самое в полном объеме относится к портфелям ценных бумаг, причем степень риска изменяется обратно пропорционально количеству включенных в портфель случайным образом видов ценных бумаг (рис.5.2.).
Общий риск портфеля состоит из двух частей:
Риск
портфеля
Диверсифицированный
риск
Общий
риск Недиверсифицированный
риск
5 10 15 20 Число финансовых
инструментов в портфеле
Рис. 5.2. Зависимость степени риска от диверсификации портфеля
- диверсифицированный (несистематический) риск, т.е. риск, который может быть элиминирован за счет диверсификации (инвестирование 1 млн.руб. в акции десяти компаний менее рискованно, нежели инвестирование той же суммы в акции одной компании);
- недиверсифицированный (систематический) риск, т.е. риск, который нельзя уменьшить путем изменения структуры портфеля.
Исследования показали, что если портфель состоит из 10-20 различных видов ценных бумаг, включенных с помощью случайной выборки из имеющегося на рынке ценных бумаг набора, то несистематический риск может быть сведен к минимуму (показано на рис. 5.2.). Таким образом, этот риск поддается элиминированию довольно несложными методами, поэтому основное внимание следует уделять возможному уменьшению систематического риска.
Существует «портфельная теория» - теория финансовых инвестиций, в рамках которой с помощью статистических методов осуществляются наиболее выгодное распределение риска портфеля ценных бумаг и оценка прибыли. Эта теория состоит из четырех элементов:
1) оценка активов;
2) инвестиционные решения;
3) оптимизация портфеля;
4) оценка результатов.
В портфельной теории, в частности, разработана модель оценки финансовых активов (САРМ), т.е. модель увязки систематического риска и доходности ценных бумаг.
Систематический риск в рамках этой модели измеряется с помощью β-коэффициентов. Каждый вид ценной бумаги имеет собственный β-коэффициент, представляющий собой индекс доходности данного актива по отношению к доходности рынка ценных бумаг в целом. Значение показателя рассчитывается по статистическим данным для каждой компании, котирующей свои ценные бумаги на бирже.
Для расчета β-коэффициента требуется совокупность показателей доходности по группе компаний за ряд периодов (Rij), где Rij – показатель доходности i-й компании (i = 1, 2, …, k) в j-м периоде (j = 1, 2, …, n). В этом случае общая формула расчета β-коэффициента для произвольной i-й компании будет иметь следующий вид:
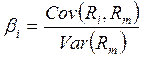(5.5.)
где:
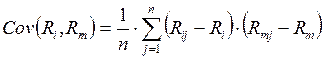(5.6.)
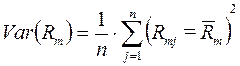(5.7.)
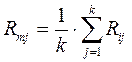(5.8.)
где Rmj – доходность в среднем на рынке ценных бумаг в j-м периоде;
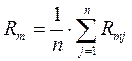(5.9.)
где Rm – доходность в среднем на рынке ценных бумаг за все периоды;
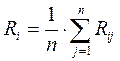(5.10.)
где Ri – доходность ценных бумаг i-й компании в среднем за все периоды.
В целом по рынку ценных бумаг β-коэффициент равен единице; большинство β-коэффициентов для отдельных компаний находится в интервале от 0,5 до 2,0. Интерпретация β-коэффициента для акций конкретной компании заключается в следующем:
β = 1 означает, что акции данной компании имеют среднюю степень риска, сложившуюся на рынке в целом;
β < 1 означает, что ценные бумаги данной компании менее рискованны, чем в среднем на рынке (так, β = 0,5 означает, что данная ценная бумага в два раза менее рискованна, чем в среднем по рынку);
β > 1 означает, что ценные бумаги данной компании более рискованны, чем в среднем на рынке;
увеличение β-коэффициента в динамике означает, что вложения в ценные бумаги данной компании становятся более рискованными;
уменьшение β-коэффициента в динамике означает, что вложения в ценные бумаги данной компании становятся менее рискованными.
Модель САРМ имеет следующий вид:
Re = Rf + β · (Rm - Rf) (5.11.)
где Re – ожидаемая доходность акций данной компании;
Rf - доходность безрисковых ценных бумаг (обычно за основу берут государственные казначейские векселя, используемые для краткосрочного (до 1 года) регулирования денежного рынка);
Rm – доходность в среднем на рынке ценных бумаг в текущем периоде;
β – бета-коэффициент данной компании.
Показатель (Rm - Rf) представляет собой рыночную премию за риск, вложенного капитала в рискованные ценные бумаги. Показатель (Re - Rf) представляет собой премию за риск вложения капитала в ценные бумаги именно данного предприятия. Модель САРМ означает, что премия за риск вложения капитала в ценные бумаги данного предприятия прямо пропорциональна рыночной премии за риск.
Важным свойством модели САРМ является ее линейность относительно степени риска. Это дает возможность определять β-коэффициент портфеля как средневзвешенную β-коэффициентов, входящих в портфель финансовых активов:
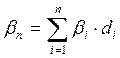(5.12.)
где βi – значение β-коэффициента i-го актива в портфеле;
βn – значение β-коэффициента портфеля;
di – доля i-го актива в портфеле;
n – число различных финансовых активов в портфеле.
Графическую интерпретацию модели САРМ составляет график «линии рынка ценных бумаг» (CML), которую можно использовать для сравнительного анализа портфельных инвестиций (рис.5.3.).
Re
Риск инвестирования
в активы компании
Рыночный риск
Систематический риск
(β-коэффициент)
Рис. 5.3. График линии рынка ценных бумаг (CML)
Как следует из модели САРМ, каждому портфелю соответствует точка в квадранте на рис 5.3. При этом возможны три варианта расположения этой точки: на линии рынка ценных бумаг, ниже или выше этой линии. В первом случае портфель называется эффективным, во втором – неэффективным, в третьем – сверхэффективным.
Возможны и другие способы применения линии рынка. В частности, отбирая финансовые активы в портфель, инвестор может находить. Какой должна быть норма дохода при заданном уровне риска.
Дата добавления: 2015-02-16; просмотров: 1541;