ДАВЛЕНИЕ НАСЫЩЕННОГО ПАРА ИНДИВИДУАЛЬНЫХ ЖИДКОСТЕЙ

Одним из важнейших свойств жидкости является давление ее насыщенно­го пара, характеризующее способность жидкости к испарению. Тепловое движение молекул жидкости ведет к отрыву их от поверхности жидкости и к переходу в газовую фазу. Однако такой отрыв может происходить только в том случае, если кинетическая энергия молекул окажется больше энергии взаимной связи между молекулами.

Часть молекул, оторвавшихся от поверхности жидкости, впоследствии снова конденсируется, другая же часть остается в газообразной фазе. Таким образом, на поверхности жидкости всегда происходит два процесса - испарение и конденсация. Если эти процессы происходят в замкнутом пространстве, то скорости испарения и конденсации выравниваются, а между жидкой и газообразной фазой наступает состояние динамическо­го равновесия.

Давление, которое молекулы пара, находящегося в равновесии с жидкой фазой, оказывают на стенки сосуда и на поверхность жидкости называется давлением насыщенного пара жидкости.

Давление пара, является функцией кинетической энергии молекул и их числа в единице объема и выражается формулой:

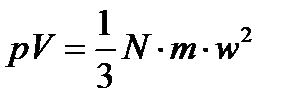(1)

р – давление пара,

N – число молекул,

V – объем пара,

m – масса молекул,

w – средняя квадратичная скорость молекул.

Согласно закону распределения Больцмана, число молекул, обладающих энергией, большей некоторого заданного предела, рассчитывается по уравнению:

(2)

где N_E – число молекул, обладающих энергией больше Е,

N – общее число молекул,

Т – абсолютная, температура,

R – постоянная Больцмана,

е – основание натуральных логарифмов.

Так как испарение обусловлено отрывом от жидкости молекул, обладающих энергией, достаточной для преодоления сил сцепления, а согласно уравнению /2/ количество таких молекул с повышением температуры возрастает в экспоненциальной зависимости, то скорость испарения быстро увеличивается с повышением температуры.

В то же самое время скорость конденсации определяется средней квадратичной скоростью молекул, для которой кинетическая теория газов дает следующее выражение:

(3)

Таким образом, скорость конденсации с повышением температуры воз­растает пропорционально квадратному корню из температуры, т.е. значительно медленнее, чем скорость испарения. Поэтому с повышением температуры сильно возрастает плотность газовой фазы, и, следовательно, давление пара.

Давление насыщенного пара чистой жидкости или твердого тела есть давление пара, находящегося в равновесии с жидкостью или твердым телом при данной температуре. Из правила фаз Гиббса следует, что система с одним компонентом и двумя сосуществующими фазами имеет только одну степень свободы.

Давление пара каждого стабильного химического вещества определяет­ся только температурой. Давление пара при данной температуре является характерным свойством соединения, знание которого необходимо для многих практических расчетов в физической химии и инженерной практике.

Так на основании данных о давлении пара Д.П. Коновалов создал классическую теорию неидеальных растворов, растворимости и фракционной перегонки. При помощи этой величины можно определить чистоту химических веществ, так как она является специфической константой каждого вещества. Знание этого свойства используется также для идентификации органических соединений.

Зависимость давления насыщенного пара от температуры выражается уравнением Клапейрона-Клаузиуса:

(4)

где DН – теплота испарения, Дж/моль или кал/моль.

DV – изменение объема при переходе 1 моль жидкости в пар.

Уравнение /4/ позволяет рассчитать любую из содержащихся в нем ве­личин, если остальные входящие в него величины известны. Например, для расчета DН необходимо располагать данными о мольных объемах пара и жидкости в условиях равновесия. Эти данные известны отнюдь не для всех случаев, а измерение их связано со значительными трудностями. Поэтому весьма ценным является то, что для некоторых частных случаев это уравнение можно упростить, сделав следующие допущения:

1. V_п » V_ж, поэтому можно пренебречь величиной V_ж

2. Пар подчиняется уравнению состояния идеальных газов:

pV = RT, n = 1

3. Теплота испарения не зависит от температуры.

С учетом этих упрощений уравнение преобразуется в уравнение 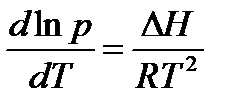/5/

(5)

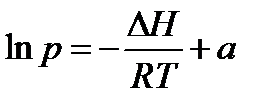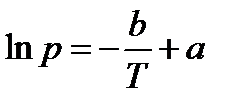Это уравнение при постоянных Н и R может быть интегрировано. Для неопределенного интеграла получаем: , или (6)

где

Величина b зависит от единиц, в которых выражено давление. Уравнение /6/ отвечает линейной зависимости в координатах. По тангенсу угла наклона прямой можно определить теплоту испарения, т.к. DН = R×tga где a – угол, образованный прямой и осью абсцисс. После определенного интегрирования получаем:

(7)

что позволяет, зная давление насыщенного пара при двух температурах, рассчитать теплоту испарения и, зная последнюю, рассчитать температуру кипения (возгонки) при заданном давлении.