Закономерности распределения магнитных полей в скважине
Процессы, протекающие в полимере под влиянием механической энергии, имеют очень большое практическое значение. Измельчение твердых полимеров, вальцевание, продавливание вязких растворов или расплавов полимеров через капиллярные отверстия, а также процессы, связанные с механическими воздействиями, широко используются в различных отраслях промышленности, перерабатывающих полимерные материалы. В процессе эксплуатации изделия, сформированные из полимеров, претерпевают различные виды деформации. При деформации в полимерах протекают механохимические процессы, которые приводят к изменению структуры и свойств полимеров. Они вызывают утомление полимеров, выражающееся в изменении их свойств, при длительных статистических или динамических воздействиях.
Действия полимеров происходит при самых разнообразных механических воздействиях. Еще в 1934 г. Штаундингер установил, что при многократном пропускании растворов полимеров через капилляр вязкость раствора вследствие деструкции макромолекул уменьшается.
Механическая деструкция также протекает при размоле и вальцевании полимеров, при интенсивном перемешивании их растворов скоростными мешалками. Полимеры деструктируются под действием ультразвука, при замораживании в водной среде, а также при деформации изделий в процессе эксплуатации.
Стойкость ВМС к механическим воздействиям зависит от приложенного напряжения, продолжительности действия нагрузки и температуры. При малом напряжении и низкой температуре полимеры разрушаются очень медленно. Увеличение напряжения при той же температуре сокращает время, необходимое для разрушения полимера. При повышенных температурах возможна термическая деструкция, которая ускоряется приложенными извне напряжениями. Во всех случаях разрушение полимера происходит в результате разрыва макромолекул.
Разрыв макромолекул приводит к образованию макрорадикалов, которые служат началом реакционной цепи и могут дальше взаимодействовать с макромолекулами полимера, вступать в реакции рекомбинации или диспропорционирования. В результате этих реакций могут изменяться молекулярная масса и структура полимеров. При механической деструкции в присутствии кислорода воздуха возникающие свободные радикалы могут инициировать цепной процесс окислительной деструкции, что приводит к еще более глубокому разрушению полимера.
Закономерности распределения магнитных полей в скважине
Вектор напряженности аномального магнитного поля и его составляющие определяются из уравнений
,
,
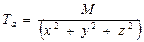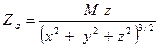(12.2)
Xa =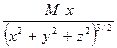 
,
Ya =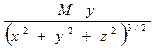 
.
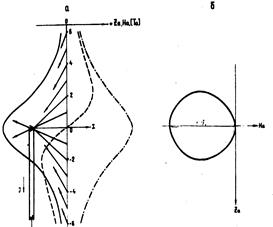
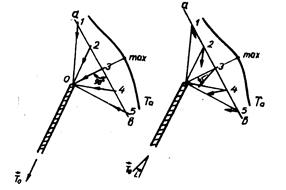
На рис. 12.3 показано распределение кривых Xа, Zа, Та векторов Та вдоль линии, расположенной в стороне от штока. Экстремальные значения кривой Zа – над кромкой стержня (максимум) и ниже ее (минимум). Все векторы Та направлены в сторону намагниченной кромки штока. Годограф векторов Та – замкнутая кривая – лемниската.
Аналогичные закономерности можно выявить и для других элементарных магнитных источников.
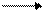
1 2 3 4 5
Рис. 12.3. Магнитное поле в скважине от штока:
а – составляющие и векторы Та, б – годограф векторов Та;
1 – На, 2 – Zа, 3 - /Та/, 4 – векторы Та, 5 – годограф Та
Тонкий пласт, намагниченный по падению и имеющий большое распространение в глубину. Пусть тонкий пласт представлен в системе координат: ось у параллельна простиранию пласта, ось z совпадает с осью скважины (рис.12.3), тогда составляющие магнитного поля могут быть определены из уравнений
,
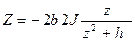(12.3)
.
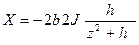Модуль вектора Та будет равен Та :
,
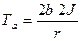где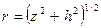 
.
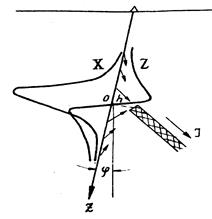
Рис. 12.4. Магнитное поле в скважине от пласта малой мощности
Местоположение верхней кромки пласта определяется сходящимся веером векторов Та, а нижней кромке тонкого пласта будет соответствовать расходящийся веер векторов.
При отклонении вектора намагниченности J от плоскости пласта на угол i уравнения (12.3) будут иметь вид
,
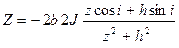(12.4)
.
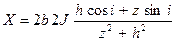Модуль вектора Та при прямой и косой намагниченности остается неизменным, он является только функцией расстояния от кромки пласта (рис.12.5). Вектор Та в случае вертикальной намагниченности будет перпендикулярен оси скважины в точках максимума кривой его модуля. При произвольной намагниченности вектор Та отклонится от перпендикуляра на угол i. Развернув весь веер на этот угол, можно определить истинное положение кромок тела.
а в
Рис. 12.5. Вектор Та и его модуль при прямом и произвольном векторе намагниченности:
а – намагниченность по оси падения пласта; в– произвольная намагниченность
Если нижняя граница пластообразного тела оказывает влияние на вид аномалии, то картина распределения магнитного поля будет намного сложнее. На рис.12.6 приведены теоретические кривые и векторные диаграммы для маломощного пласта, ограниченного по падению. Рассмотрены два пласта с вертикальной намагниченностью, но различного падения. Как видно из приведенных графиков и направлений векторов, пересечение полных векторов не совпадает с границами пласта. Расхождение тем больше, чем дальше от скважины расположен пласт.
Магнитное поле шара. Если магнитный источник сферической формы удален по перпендикуляру от ствола скважины на расстоянии
h = ( х2 + у2)1/2,
то при осевой схеме ориентации датчиков составляющие магнитного потенциала будут равны
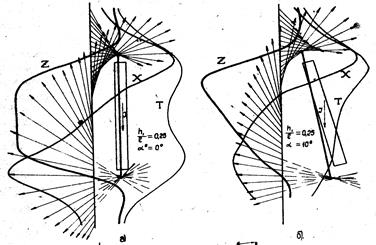
Рис.12.6. Магнитное поле тонких пластов, ограниченных по падению:
а – вертикальное падение; в – наклонное падение
,
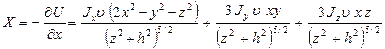(12.5)
.
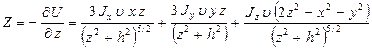В случае, если скважина проходит через центр сферы, то выражение (12.5) упрощается:
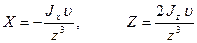–вне сферы;
(12.6)
– внутри сферы.
На рис. 12.7 приведены графики Zа и векторы Та для шара по вертикальным линиям наблюдения, расположенным вне сферы и внутри сферы. График Zа центрального пересечения четко отражает размеры сферы и определяет ее местоположение. Графики Zа краевого пересечения, расположенные вне сферы, могут дать информацию о стороне расположения магнитного источника.
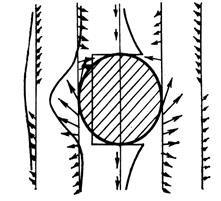
Рис.12.7. Кривые Zа и векторы Та по вертикальной линии наблюдений для шара
Дата добавления: 2015-02-16; просмотров: 960;