Напряженность поля в диэлектрике

Рисунок 3.6 - К вычислению электростатического поля в диэлектрике.

Поместим пластину однородного диэлектрика в электрическое поле 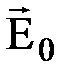меж­ду двумя бесконечными парал­лельными разноименно заряженными плоскостями (рис.3.6). Под действием внешнего поля диэлектрик поля­ризуется, в результате чего, на боковой грани диэлектрика, обращенной к положительной плоскости, появляется избы­ток отрицательных зарядов с поверхностной плотностью -s¢, а на противопо­ложной - избыток положительных заря­дов с поверхностной плотностью +s¢. Эти не скомпенсиро­ванные заряды называются связанными и они создают свое собст­венное добавочное поле 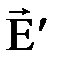, направленное против внешнего поля 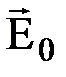. На рисунке 3.6 сплошными стрелками обозначены силовые линии внешнего поля 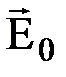, а пунктирными - поля 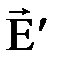. Поэтому результирующая напряженность поля 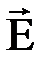в диэлектрике меньше 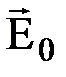на величину : .

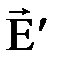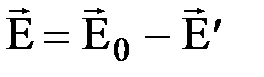Напряженность собственного добавочного поля диэлектрика 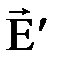можно определить с помо­щью формулы для напряженно­сти поля между параллельными бесконечными заря­жен­ными плоскостями: 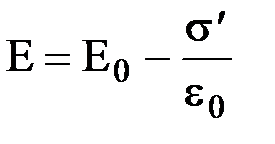. Определим поверхностную плотность связанных зарядов s¢. Для однородного диэлектрика, занимающего объем V, полный дипольный момент равен 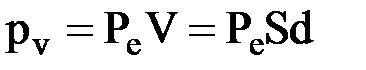, где S ‑ площадь боковой грани пластины, d - ее толщина. С другой стороны, 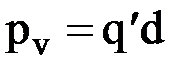, где 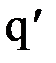‑ связанный заряд боковой грани. Поскольку 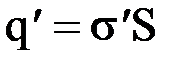, то . 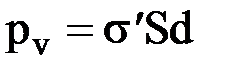Отсюда имеем 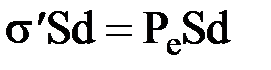, следовательно 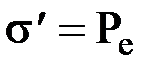. Отсюда, плотность связанных зарядов s¢ равна поляризованности диэлектрика Р_е. Таким об­разом, напряженность поля внутри диэлектрика можно записать в виде: 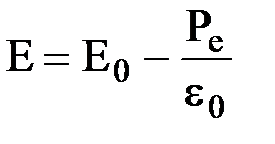. Так как Р_е=e₀æЕ, то 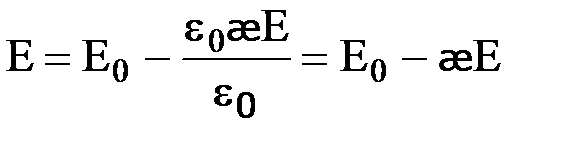. Отсюда 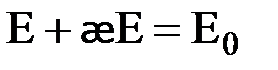и 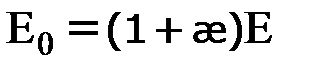. Ранее было показано, что относительная диэлектрическая проницаемость среды e есть от­ношение сил взаимодействия зарядов в вакууме F₀ и в данной среде F. Так как напряженно­сти поля пропорциональны этим силам, то 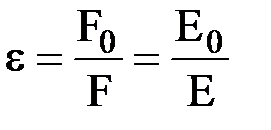. Подставив это соотношение в последнюю формулу, получим: .

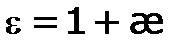Таким образом, диэлектрическая проницаемость среды показывает во сколько раз напряженность поля в диэлектрике уменьшается по сравнению с напряженностью внешнего поля, а также количест­вен­но характеризует способность диэлектрика поляризоваться в электрическом поле.