Примеры решения задач. Задача 1. Шарик массой m = 40мг, имеющий положительный заряд q=1нКл, движется со скоростью v = 10 см/с
Задача 1. Шарик массой m = 40мг, имеющий положительный заряд q=1нКл, движется со скоростью v = 10 см/с. На какое расстояние r может приблизиться шарик к положительному точечному заряду q0 = 1,33нКл?
Решение. Если в поле неподвижного заряда q1 происходит медленное перемещение заряда q2 из точки В в точку С, то работа сил поля
.
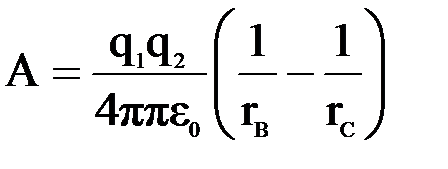Если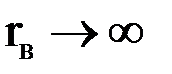 
, то rC = r12 и 
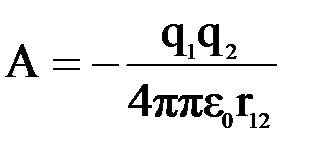(т.е. появился знак «минус»). Работа консервативных сил электрического поля равна убыли потенциальной энергии системы заряженных тел, т.е. A = -(U12 - U∞). Поэтому полагая энергию взаимодействия бесконечно удалённых зарядов равной нулю, получим для потенциальной энергии взаимодействия системы двух зарядов 
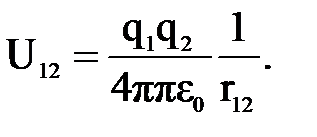Во время движения шарика его кинетическая энергия 
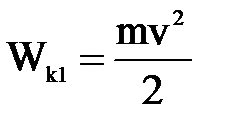, при приближении к заряду q2 на предельное расстояние r12 кинетическая энергия Wk2 = 0. Работа 
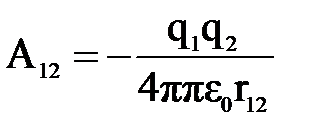; A = 
.
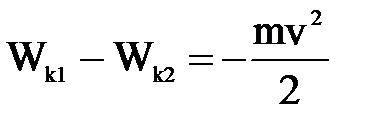Таким образом,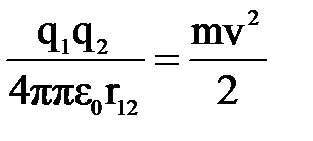 
, откуда 
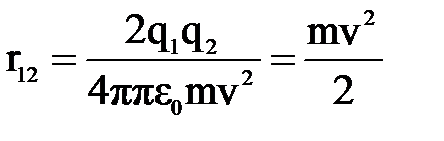; r12=r=6см.
Задача 2.Тонкое кольцо радиуса R имеет заряд q, неравномерно распределённый по кольцу. Найти работу электрических сил при перемещении точечного заряда q1 из центра кольца по произвольному пути в точку, находящуюся на оси кольца на расстоянии l от его центра.
Решение:. Поскольку центр кольца равноудалён от всех точек на кольце, то независимо от распределения заряда по кольцу, потенциал его центра равен
.
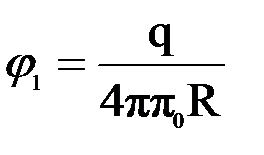Потенциал точки, лежащей на оси кольца, в свою очередь равен
.
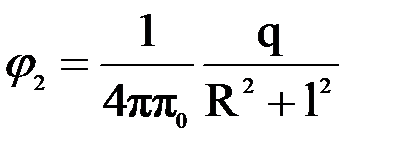Работа по перемещению заряда равна A = q1(φ1 - φ2).
Следовательно, работа по перемещению заряда равна
.
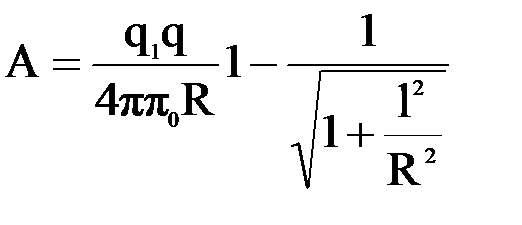Задача 3.Заряд q равномерно распределён по объёму шара радиуса R. Полагая диэлектрическую проницаемость всюду равной единице, найти потенциал:
а) в центре шара;
б) внутри шара, как функцию расстояния r от его центра.
Решение. Воспользуемся тем, что потенциал равен работе электростатических сил при переносе единичного положительного заряда из данной точки в бесконечность. Электрическое поле внутри шара равно: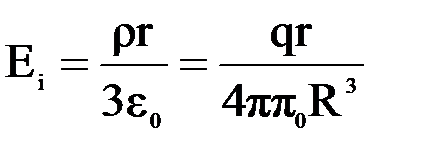 
. Поле вне шара определяется формулой: 
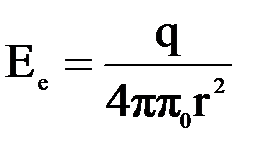. Потенциал в точке, расположенной на расстоянии r от центра шара, равен:
.
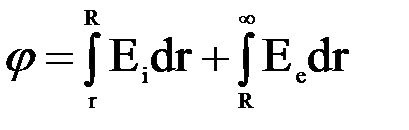Интегрирование приводит к ответу:
.
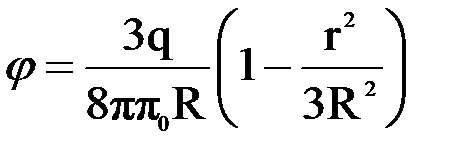Отсюда потенциал в центре шара равен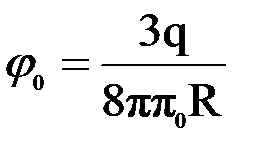 
.
Ответ: а)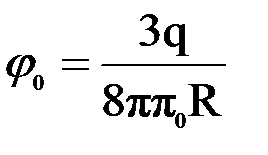 
; б)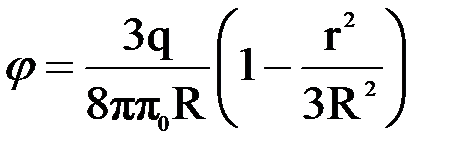 
.
Задача 4.Потенциал электрического поля имеет вид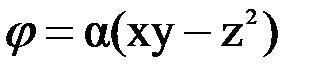 
, где α− постоянная. Найти проекцию напряжённости электрического поля в точке М 
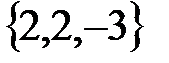на направление вектора 
= 
.
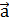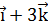Решение. Проекции напряжённости поля найдём с помощью формулы , связывающей напряженность и потенциал
Ex = -αy, Ee = -αx, Ez = 2αz.
Проекция Еa напряжённости на направление вектора 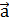может быть выражена через скалярное произведение: Ea=( 
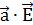/a) (модуль вектора 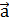равен 10). Отсюда находим искомую проекцию: 
.
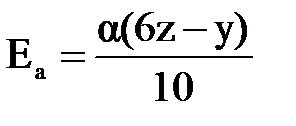Подстановка координат точки М приводит к окончательному ответу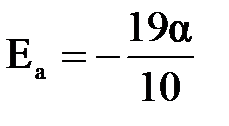 
Ответ: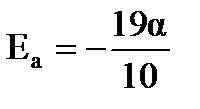 
.
Задача 5.Электрон со скоростью v =1,83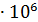 
м/с влетел в однородное электрическое поле в направлении, противоположном вектору напряженности поля. Какую разность потенциалов U должен пройти электрон, чтобы обладать энергией Еi= 13,6 эВ? (Обладая такой энергией, электрон при столкновении с атомом водорода может ионизировать его. Энергия 13,6 эВ называется энергией ионизации водорода.)
Решение: Электрон должен пройти такую разность потенциалов U, чтобы приобретенная при этом энергия Wp в сумме с кинетической Wk, которой обладал электрон перед вхождением в поле, составила энергию, равную энергии ионизации Ei, т.е. Wp+Wk=Ei. Выразив в этой формуле Wp=eU и Wk=mv2/2, получим eU+mv2=Ei. Отсюда U=(2Ei – mv2)/2e = 4,15 В.
Задача 6. Покажите, что напряжение пробоя для сферического проводника в воздухе пропорционально радиусу сферы и рассчитайте напряжение пробоя в воздухе для сферы диаметром 1,0 см.
Решение: Во многих установках используют очень высокие напряжения. Проблема, связанная с этим, заключается в том, что поля больших напряженностей могут ионизовать воздух — электрическое поле вырывает электроны из атомов кислорода и азота. Воздух становится проводящим, и это препятствует поддержанию высокого напряжения из-за утечки заряда. Электрический пробой воздуха наступает при напряженности поля ~3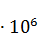 
В/м.
Электрический потенциал поверхности сферического проводника равен φ=q/4πε0R, а напряженность поля вблизи поверхности равна E=q/4πε0R2. Отсюда U=RE (вблизи поверхности сферического проводника). При R=0,5 cм=5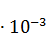 
м напряжение пробоя в воздухе составит U=(5 
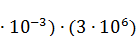=15000 В.
Из этого примера ясно, почему выводы установок высокого напряжения делают большими. Понятно также, почему пробой (искрение) возникает на шероховатостях и остриях (области малого радиуса кривизны) и почему обычно проводники стараются делать как можно более гладкими.
Выводы:Потенциал является энергетической характеристикой и наравне с напряженностью используется для описания электрического поля. Следует учитывать, что потенциал – алгебраическая величина, т.е. он может быть как положительным, так и отрицательным.
Контрольные вопросы второго уровня (сборник задач)
1. Точечный заряд q=10 нКл, находясь в некоторой точке поля, обладает потенциальной энергией Wp=10 мкДж. Найти потенциал φ этой точки поля. [1 кВ]
2. Поле создано точечным зарядом q=1 нКл. Определить потенциал φ поля в точке, удаленной от заряда на расстояние r =20 см. [45 В]
3. Определить потенциал φ электрического поля в точке, удаленной от зарядов q1= - 0,2 мкКл и q2= 0,5 мкКл соответственно на r1=15 см и r2=25 см.[6 кВ]
4. Заряды q1=1 мкКл и q2= - 1 мкКл находятся на расстоянии d=10 см. Определить напряженность Е и потенциал φ поля в точке, удаленной на расстояние r =10 см от первого заряда и лежащей на линии, проходящей через первый заряд перпендикулярно направлению от q1 к q2. [664 кВ/м; 26,4 кВ]
5. Металлический шар радиусом r = 5 см несет заряд q = 1 нКл. Шар окружен слоем эбонита толщиной d=2 см. Вычислите потенциал электрического поля на расстоянии: 1)r1 = 3 см; 2)r2=6 см; 3)r3=9 см от центра шара. Постройте график зависимости φ от r. [146 В; 136 В; 100 В]
6. Металлический шар радиусом R = 10 см заряжен до потенциала φ1= 300 В. Какой потенциал будет иметь этот шар, если его окружить сферической проводящей заземленной оболочкой радиусом r=15 см? [100 В]
7. При перемещении заряда q=20 нКл между двумя точками поля внешними силами была совершена работа А= 4 мкДж. Определить работу А1 сил поля и разность Δφ потенциалов этих точек поля. [- 4 мкДж; 200 В]
8. Положительные заряды q1= 3 мкКл и q2= 20 нКл находятся в вакууме на расстоянии 1,5 м друг от друга. Определите работу, которую нужно совершить, чтобы сблизить заряды до расстояния 1 м. [0,18 мДж]
9. Тонкий стержень согнут в полукольцо. Стержень заряжен с линейной плотностью τ= 133 нКл/м. Какую работу надо совершить, чтобы перевести заряд q = 6,7 нКл из центра полукольца в бесконечность? [25,2 мкДж)
10. Тонкий стержень согнут в кольцо радиусом R = 10 см и заряжен с линейной плотностью τ = 300 нКл/м. Какую работу надо совершить, чтобы перенести заряд q= 5 нКл из центра кольца в точку А, расположенную на оси кольца на расстоянии l= 20 см от его центра? [47 мДж]
11. Найдите потенциальную энергию системы трех точечных зарядов q1 = -10 нКл, q2 = 20 нКл и q3 = -30 нКл, расположенных в вершинах равностороннего треугольника со стороной а = 5 см. [18 мкДж]
12. Определите потенциальную энергию системы четырех точечных зарядов, расположенных в вершинах квадрата со стороной a=10 см. Заряды одинаковы по абсолютной величине q= 10 нКл, но два из них отрицательны. Рассмотреть два возможных случая расположения зарядов. [12,7 мкДж; -12,7 мкДж]
13. Заряд равномерно распределен по бесконечной плоскости с поверхностной плотностью σ = 10 нКл/м2. Разность потенциалов двух точек поля, одна из которых находится на плоскости, а другая удалена от нее на некоторое расстояние а, составляет Δφ = 56,6 В. Определите это расстояние. [10 см]
14. Две параллельные заряженные плоскости, поверхностные плотности заряда которых σ1 = 2 мкКл/м2 и σ2 = -0,8 мкКл/м2, находятся на расстоянии d =0,6 см друг от друга. Определите разность потенциалов Uмежду плоскостями. [9,5 кВ]
15. Поле образовано бесконечной равномерно заряженной плоскостью с поверхностной плотностью заряда σ = 40 нКл/м2. Определите разность потенциалов Uдвух точек поля, отстоящих от плоскости на r1 = 15 см и r3 = 20 см. [113 В]
16. Поле образовано точечным диполем с электрическим моментом p = 200 нКл 
м. Определите разность потенциалов U двух точек поля, расположенных симметрично относительно диполя на его оси на расстоянии r =40 см от центра диполя. [22,5 кВ]
17. Электрическое поле образовано бесконечно длинной заряженной нитью, линейная плотность заряда которой τ = 20 нКл/м. Определите разность потенциалов Uдвух точек поля, отстоящих от нити на расстояния r1 = 8 см и r2= 12 см. [146 В]
18. Тонкая квадратная рамка равномерно заряжена с линейной плотностью заряда τ = 200 пКл/м. Определите потенциал φ поля в точке пересечения диагоналей. [12,7 В]
19. Пылинка массой m = 200 нг, несущая на себе заряд q = 40 нКл, влетела в электрическое поле в направлении силовых линий. После прохождения разности потенциалов U = 200 В пылинка имела скорость 10 м/с. Определите скорость пылинки до того, как она влетела в поле. [4,5 м/с]
20. Электрон, обладавший кинетической энергией 10 эВ, влетел в однородное электрическое поле в направлении силовых линий поля. Какой скоростью будет обладать электрон, пройдя в этом поле разность потенциалов U= 8 В? [0,84 Мм/с]
21. Электрон с энергией 400 эВ (в бесконечности) движется вдоль силовой линии по направлению к поверхности металлической заряженной сферы радиусом R=10 см. Определите минимальное расстояние а, на которое приблизится электрон к поверхности сферы, если заряд ее q = -10 нКл. [0,225 м]
22. Ион атома лития Li+ прошел разность потенциалов U1 = 400 В, ион атома натрия Na+ — разность потенциалов U2 = 300 В. Найдите отношение скоростей этих ионов. [2,1]
23. Бесконечная плоскость заряжена отрицательно с поверхностной плотностью σ = 35,4 нКл/м2. По направлению силовой линии поля, созданного плоскостью, летит электрон. Определите минимальное расстояние, на которое может подойти к плоскости электрон, если на расстоянии l = 5 см он имел кинетическую энергию 80 эВ. [1 см]
24. Электрон влетел в плоский конденсатор, находясь на одинаковом расстоянии от каждой пластины и имея скорость 10 Мм/с, направленную параллельно пластинам. Расстояние между пластинами d= 2 см, разность потенциалов, приложенная к пластинам, U=22,5 В. Какую наименьшую длину должны иметь пластины, чтобы электрон не вылетел из конденсатора? [10 см]
25. Бесконечная плоскость равномерно заряжена с поверхностной плотностью заряда σ = -2 нКл/м2. Определите численное значение и направление градиента потенциала электрического поля, созданного этой плоскостью. [113 В/м]
26. Электрическое поле создано положительным точечным зарядом. Потенциал поля в точке, удаленной от заряда на r = 6 см, φ = 12 В. Определите величину и направление градиента потенциала в этой точке. [200 В/м]
27. Бесконечная тонкая прямая нить несет равномерно распределенный по длине нити заряд τ = -2 нКл/м. Каков градиент потенциала в точке, удаленной на расстояние r =10 см от нити? Укажите направление градиента потенциала. [360 В/м[
28. Может ли электростатическое поле иметь вид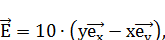 
где 
и 
орт-векторы вдоль соответствующих осей координат? [Нет; указание: найдите циркуляцию Е по произвольному контуру]
29. Электростатическое поле имеет вид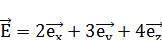 
. Является ли это поле однородным? Найдите потенциал этого поля φ(r). [Да; φ=-(2x+3y+4z)]
30. Потенциал поля, создаваемого некоторой системой зарядов, имеет вид φ=-(2x2+3y+4z). Найдите напряженность поля 
и ее модуль. Какую форму имеют эквипотенциальные поверхности? [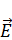 
=-(x +y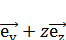 
) ; E=4 
]
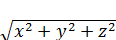Контрольные вопросы третьего уровня (тесты)
1. Какое из приведенных ниже выражений есть определение потенциала электрического поля?
| а)j = ; | б) j = ; | в)j =ji; |
| г) ; | д)A = q(j1 – j2). |
2. Поставьте в соответствие потенциалу заряженного тела его математическое выражение.
| Потенциал | Математическое выражение | ||||
| а) потенциал точечного заряда | 1) j = | ||||
| б) потенциал внутри заряженной сферы радиуса r | 2) j = | ||||
| в) потенциал системы точечных зарядов | 3) j = const | ||||
| г) потенциал поля диполя | 4) j= | ||||
| а) ; | б) ; | в) ; | г) __ | ||
3. Какое из приведенных ниже выражений определяет энергию диполя в электрическом поле?
| а)W = ; | б) W = qj; | в) W =–pE cosa; | г)W= qiji. |
4.
| Е |
| p |
| б) |
| Е |
| p |
| а) |
| Е |
| p |
| в) |
При какой ориентации электрический диполь в однородном электрическом поле находится в положении устойчивого равновесия относительно поворотов?
5. На рисунке показаны силовые линии и две эквипотенциальные поверхности 1 и 2 в электростатическом поле. Какие точки имеют одинаковые потенциалы?
| A |
| D |
| C |
| B |
| а) А, В, С; | б) B и С; | в) А и D; | г) B и D; | д) С и D. |
6. Какое из нижеприведенных выражений дает связь между напряженностью электростатического поля и потенциалом в неоднородном электрическом поле?
| а) ; | б) ; | в) ; |
| г) ; | д) . |
7. Укажите номера всех схем, на которых потенциал поля в центре правильного шестиугольника равен нулю.
1) 2) 3) 4)
| а) 1, 2, 3; | б) 1, 4; | в) 1, 3, 4; | г) 2, 3, 4; | д) 2,3. |
8. Какой из нижеприведенных графиков качественно отражает зависимость потенциала от расстояния для уединенной металлической заряженной сферы радиуса R?
а) б) в) г)
9. В каких из нижеприведенных случаев разность потенциалов между точками А и B равна нулю?
1) 2) 3) 4) 5)
| а) 1, 5; | б) 2, 3; | в) 2, 4; | г) 2; | д) 4. |
10. Указать ошибочную запись в выражениях, дающих работу А сил электростатического поля при перемещении заряда q из точки 1 в точку 2.
| x |
| +q |
| –q |
| 1) q(φ1-φ2) ; | 2) ; | 3) ; | |||||
| 4) ; | 5) . | ||||||
| а) 1, 2, 3; | б) 2; | в) 3; | г) 3, 2; | д) 4; | е) 2, 5. | ||
Дата добавления: 2015-02-13; просмотров: 12531;