Правила Кирхгофа для разветвленных цепей. Обобщенный закон Ома (см

Обобщенный закон Ома (см. (100.3)) позволяет рассчитать практически любую сложную цепь. Однако непосредственный расчет разветвленных цепей, содержащих несколько замкнутых контуров (контуры могут иметь общие участки, каждый из контуров может иметь несколько источников тока и т. д.), довольно сложен. Эта задача решается более просто с помощью двух правая Кирхгофа[2].

Любая точка разветвления цепи, в которой сходится не менее трех проводников с током, называется узлом. При этом ток, входящий в узел, считается положительным, а ток, выходящий из узла, — отрицательным.

Первое правило Кирхгофа: алгебраическая сумма токов, сходящихся в узле, равна нулю:

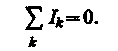
Например, для рис. 148 первое правило Кирхгофа запишется так:

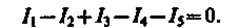
Первое правило Кирхгофа вытекает из закона сохранения электрического заряда. Действительно, в случае установившегося постоянного тока ни в одной точке проводника и ни на одном его участке не должны накапливаться электрические заряды. В противном случае токи не могли бы оставаться постоянными.

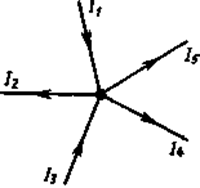
Рис. 148

Второе правило Кирхгофа получается из обобщенного закона Ома для разветвленных цепей. Рассмотрим контур, состоящий из трех участков (рис. 149).

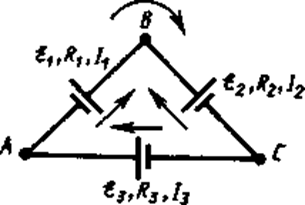
Рис. 149

Направление обхода по часовой стрелке примем за положительное, отметив, что выбор этого направления совершенно произволен. Все токи, совпадающие по направлению с направлением обхода контура, считаются положительными, не совпадающие с направлением обхода — отрицательными. Источники тока считаются положительными, если они создают ток, направленный в сторону обхода контура. Применяя к участкам закон Ома (100.3), можно записать:

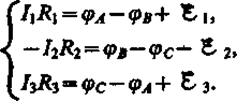
Складывая почленно эти уравнения, получим

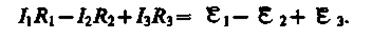(101.1)

Уравнение (101.1) выражает второе правило Кирхгофа: в любом замкнутом контуре, произвольно выбранном в разветвленной электрической цепи, алгебраическая сумма произведений сил токов I_i на сопротивления R_i, соответствующих участков этого контура равна алгебраической сумме э.д.с. x_k, встречающихся в этом контуре:

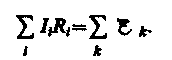(101.2)

При расчете сложных цепей постоянного тока с применением правил Кирхгофа необходимо:

1. Выбрать произвольное направление токов на всех участках цепи; действительное направление токов определяется при решении задачи: если искомый ток получится положительным, то его направление было выбрано правильно, отрицательным — его истинное направление противоположно выбранному.

2. Выбрать направление обхода контура и строго его придерживаться; произведение IRположительно, если ток на данном участке совпадает с направлением обхода, и, наоборот, э.д.с., действующие по выбранному направлению обхода, считаются положительными, против — отрицательными.

3. Составить столько уравнений, чтобы их число было равно числу искомых величин (в систему уравнений должны входить все сопротивления и э.д.с. рассматриваемой цепи); каждый рассматриваемый контур должен содержать хотя бы один элемент, не содержащийся в предыдущих контурах, иначе получатся уравнения, являющиеся простой комбинацией уже составленных.

В качестве примера использования правил Кирхгофа рассмотрим схему (рис. 150) измерительного моста Уитстона[3].

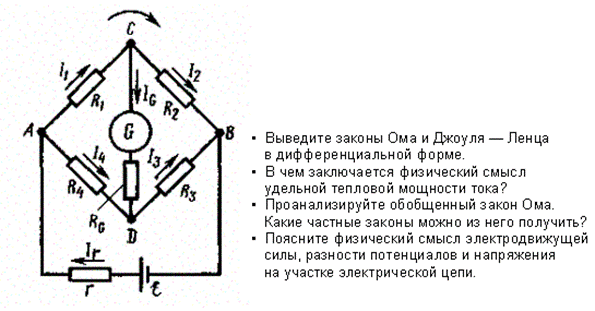
Рис. 150

Сопротивления R₁, R₂, R₃и R₄образуют его «плечи». Между точками А и Вмоста включена батарея с э.д.с. x и сопротивлением r, между точками С и D включен гальванометр с сопротивлением R_G. Для узлов А. В и С, применяя первое правило Кирхгофа, получим

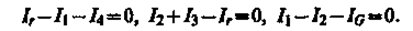(101.3)

Для контуров АСВA, ACDA и CBDC, согласно второму правилу Кирхгофа, можно записать:

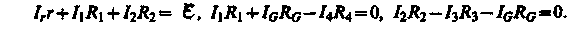(101.4)

Если известны все сопротивления и э.д.с,, то, решая полученные шесть уравнений, можно найти неизвестные токи. Изменяя известные сопротивления R₂, R₃и R₄можно добиться того, чтобы ток через гальванометр был равен нулю (I_G = 0). Тогда из (101.3) найдем

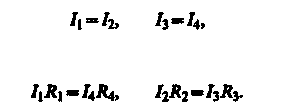(101.6)

Из (101.5) и (101.6) вытекает, что

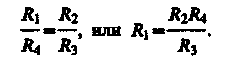(101.7)

Таким образом, в случае равновесного моста (I_G = 0) при определении искомого сопротивления R₁Э.Д.С. батареи, сопротивления батареи и гальванометра роли не играют.

На практике обычно используется реохордный мост Унтстоиа (рис. 151), где сопротивления R₃ и R₄ представляют собой длинную однородную проволоку (реохорд) с большим удельным сопротивлением, так что отношение R₃/R₄можно заменить отношением l₃/l₄.

Рис. 151

Тогда, используя выражение (101.7), можно записать

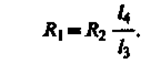(101.8)

Длины l₃ и l₄ легко измеряются по шкале, а R₂всегда известно. Поэтому уравнение (101.8) позволяет определить неизвестное сопротивление R₁.

Задачи

12.1. По медному проводнику сечением 1 мм² течет ток; сила тока 1 А. Определить среднюю скорость упорядоченного движения электронов вдоль проводника, предполагая, что на каждый атом меди приходится один свободный электрон. Плотность меди 8,9 г/см³. [74 мкм/с]

12.2. Определить, во сколько раз возрастет сила тока, проходящего через платиновую печь, если при постоянном напряжении на зажимах ее температура повышается от t₁ =20°С до t₂ = 1200°С. Температурный коэффициент сопротивления платины принять равным 3,65×10^-3 К^-1. [В 5 раз]

12.3. По медному проводу сечением 0,3 мм² течет ток 0,3 А. Определить силу, действующую на отдельные свободные электроны со стороны электрического поля. Удельное сопротивление меди 17 нОм×м. [2,72×10 ^-21 Н]

12.4. Сила тока в проводнике сопротивлением 10 Ом равномерно убывает от I₀ =3 А до I = 0 за 30 с. Определить выделившееся за это время в проводнике количество теплоты. [900 Дж]

12.5. Плотность электрического тока в алюминиевом проводе равна 5 А/см². Определить удельную тепловую мощность тока, если удельное сопротивление алюминия 26 нОм-м. [66 Дж/(м³.с)]

12.6. Определить внутреннее сопротивление r источника тока, если во внешней цепи при силе тока I₁ = 5 А выделяется мощность P₁ = 10 Вт, а при силе тока I₂ = 8 А — мощность Р₂ = 12 Вт. [0.17 Ом]

12.7. Три источника тока с э.д.с. E₁ = 1,8 В, E₂ = 1,4 В и E₃ = 1,1 В соединены накоротко одноименными полюсами. Внутреннее сопротивление первого источника r₁ =0,4 Ом, второго— г₂ = 0,6 Ом. Определить внутреннее сопротивление третьего источника, если через первый источник идет ток I₁ = 1,13 А. [0,2 Ом]