Молекулярно-кинетической теории
Рассмотрим некоторые явления, экспериментально подтверждающие основные положения и выводы молекулярно-кинетической теории.
1.Броуновское движение. Шотландский ботаник Р. Броун (1773—1858), наблюдая под микроскопом взвесь цветочной пыльцы в воде, обнаружил, что частицы пыльцы оживленно и беспорядочно двигались, то вращаясь, то перемещаясь с места на место, подобно пылинкам в солнечном луче. Впоследствии оказалось, что подобное сложное зигзагообразное движение характерно для любых частиц малых размеров («1 мкм), взвешенных в газе или жидкости. Интенсивность этого движения, называемого броуновским, повышается с ростом температуры среды, с уменьшением вязкости и размеров частиц (независимо от их химической природы). Причина броуновского движения долго оставалась неясной. Лишь через 80 лет после обнаружения этого эффекта ему было дано объяснение: броуновское движение взвешенных частиц вызывается ударами
молекул среды, в которой частицы взвешены. Так как молекулы движутся хаотически, то броуновские частицы получают толчки с разных сторон, поэтому и совершают движение столь причудливой формы. Таким образом, броуновское движение является подтверждением выводов молекулярно-кинетической теории о хаотическом (тепловом) движении атомов и молекул.
2.Опыт Штерна. Первое экспериментальное определение скоростей молекул выполнено немецким физиком О. Штерном (1888—1970). Его опыты позволили также оценить распределение молекул по скоростям. Схема установки Штерна представлена на рис. 70.
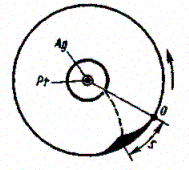
Рис. 70
Вдоль оси внутреннего цилиндра с щелью натянута платиновая проволока, покрытая слоем серебра, которая нагревается током при откачанном воздухе. При нагревании серебро испаряется. Атомы серебра, вылетая через щель, попадают на внутреннюю поверхность второго цилиндра, давая изображение щели О. Если прибор привести во вращение вокруг общей оси цилиндров, то атомы серебра осядут не против щели, а сместятся от точки Она некоторое расстояние s. Изображение щели получается размытым. Исследуя толщину осажденного слоя, можно оценить распределение молекул по скоростям, которое соответствует максвелловскому распределению.
Зная радиусы цилиндров, их угловую скорость вращения, а также измеряя s, можно вычислить скорость движения атомов серебра при данной температуре проволоки. Результаты опыта показали, что средняя скорость атомов серебра близка к той, которая следует из максвелловского распределения молекул по скоростям.
3. Опыт Ляммерт. Этот опыт позволяет более точно определить закон распределения молекул по скоростям. Схема вакуумной установки приведена на рис. 71. Молекулярный пучок, сформированный источником, проходя через щель, попадает в приемник. Между источником и приемником помещают два диска с прорезями, закрепленных на общей оси. При неподвижных дисках молекулы достигают приемника, прохода через прорези в обоих дисках. Если ось привести во вращение, то приемника достигнут только те прошедшие прорезь в первом диске молекулы, которые затрачивают дня пробега между дисками время, равное или кратное времени оборота диска. Другие же молекулы задерживаются вторым диском. Меняя угловую скорость вращения дисков
и измеряя число молекул, попадающих в приемник, можно выявить закон распределения молекул по скоростям. Этот опыт также подтвердил справедливость максвелловского распределения молекул по скоростям.
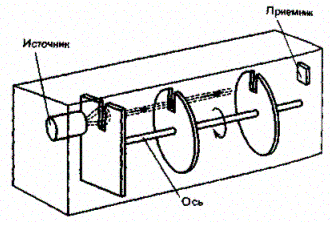
Рис. 71
4.Опытное определение постоянной Авогадро. Воспользовавшись идеей распределения молекул по высоте (см. формулу (45.4)), французский ученый Ж. Перрен (1870—1942) экспериментально определил значение постоянной Авогадро. Исследуя под микроскопом броуновское движение, он убедился, что броуновские частицы распределяются по высоте подобно молекулам газа в поле тяготения. Применив к ним больцмановское распределение, можно записать
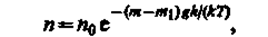
где m— масса частицы, m1— масса вытесненной ею жидкости; 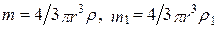 (r— радиус частицы, r— плотность частицы, r1— плотность жидкости). Если n1 и n2 — концентрации частиц на уровнях h1и h2, a k = R/NA,то
(r— радиус частицы, r— плотность частицы, r1— плотность жидкости). Если n1 и n2 — концентрации частиц на уровнях h1и h2, a k = R/NA,то
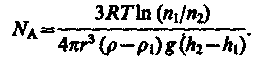
Значение NА, получаемое из работ Ж. Перрена, соответствовало значениям, полученным в других опытах, что подтверждает применимость к броуновским частицам распределения (45.4).
Дата добавления: 2015-02-13; просмотров: 723;
