Неполной взаимозаменяемости

Способ максимума-минимума предполагает, что в процессе сборки узла или обработки детали возможно одновременное сочетание наибольших увеличивающих и наименьших уменьшающих размеров или обратное их сочетание. Однако практически такое сочетание маловероятно, так как отклонение размеров в основном группируется около середины поля допуска.

Метод неполной взаимозаменяемости допускает приемлемый процент изделий, у которых замыкающее звено выйдет за поле допуска, но при этом существенно увеличивается допуск составляющих звеньев. Метод исходит из предположения, что сочетания действительных размеров составляющих звеньев, входящих в размерную цепь, носят случайный характер, и большая часть значений звеньев группируется около координаты середины поля допуска. Для такого метода применяется вероятностный способ расчета.

Предположим, что погрешности изготовления всех звеньев распределены по нормальному закону (закону Гаусса) и центр группирования деталей совпадает с координатой середины поля допуска. Тогда можно принять Т_i = 6s_i (с вероятностью 99,73 %), где Т_i – допуск i-го звена, s_i – среднеквадратическое отклонение размеров i-х деталей после их изготовления. При этом только у 0,27 % изделий размеры могут выходить за пределы поля допуска (рис. 6.4).

Из теории вероятности дисперсия суммы равна сумме дисперсий, следовательно, для размерной цепи:

s_D² = s₁² + s₂² +…+ s_n², в общем виде:

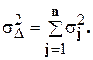
Отсюда 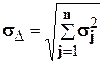, где s_D - среднее квадратичное отклонение замыкающего звена. Отношение допускаемого отклонения от центра группирования х к среднему квадратичному отклонению s принято называть коэффициентом риска t. Для замыкающего звена х/s_D = t_D. В нашем случае допустимое отклонение от центра группирования будет равно х = Т_D/2, отсюда t_D = Т_D/2s_D или s_D = Т_D/2 t_D. Выражая дисперсию через допуск, получим:

.

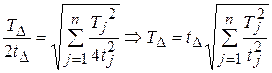Однако в условиях реального производства погрешность составляющих звеньев может подчиняться не только закону Гаусса, но и другим законам с симметричным распределением, а выход размеров замыкающего звена за границы поля допуска может быть позволен не более чем 0,27 %. Поэтому в общем случае:

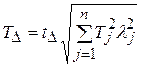, (6.5)

где t_D - коэффициент риска, который выбирается из таблицы значений функции Лапласа F(t) в зависимости от выбранного процента брака Р. Ряд значений коэффициента t_D представлен в табл. 9.

Т а б л и ц а 9

Значения коэффициента t

% брака Р			4,5		2,5		1,5		0,5	0,27	0,1	0,01
tΔ		1,05		2,14	2,24	2,33	2,43	2,57	2,81		3,29	3,89

 

– относительное среднеквадратическое отклонение, характеризующее закон распределения; w_j – зона предельного рассеивания случайной величины. В случае нормального закона l_j² = 1/9, в случае закона Симпсона l_j² = 1/6, в случае закона равной вероятности l_j² = 1/3.

Исходя из того, что все звенья размерной цепи должны иметь примерно одинаковый квалитет, находим величину k–количество единиц допуска.

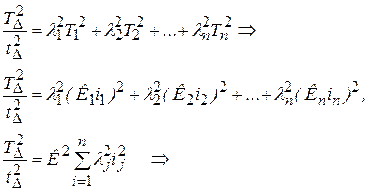
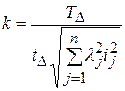. (6.6)

 

Пример: Проведем расчет той же размерной цепи, изображенной на рис. 6.3, методом неполной взаимозаменяемости. Примем допустимый процент риска Р = 2,1 % (t_D = 2,3). Предположим, что отклонения всех деталей распределены по закону Симпсона, тогда l_j² = 1/6.

По формуле (6.6) получим (k = 40 соответствует 9-му квалитету, а k = 64 соответствует 10-му квалитету). Выбираем ближайший 9 квалитет для всех звеньев.

Предельные отклонения звеньев А₁ и А₂ назначаем как и в предыдущем методе по ±IT/2 и h соответственно. Предельное отклонение звена А₃ рассчитываем на основе зависимости:

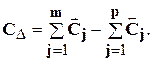(6.7)

где С_D - середина координаты поля допуска замыкающего звена; С_j – координаты середин допусков составляющих звеньев.

Подставив значения получим:

+50 = 0 – (-31) – С₃ Þ С₃ = -19 мкм;

В_D = С_D + Т_D/2 = -19 + 18 = -1 мкм;

Н_D = С_D – Т_D/2 = -19 – 18 = -37 мкм.

Данные расчетов для удобства сведем в табл. 10.

Для проверки правильности выбора допусков рассчитаем допуск замыкающего звена с заданной вероятностью:

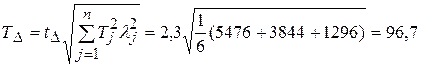< 100 мкм.

Т а б л и ц а 10

Расчет размерной цепи методом неполной взаимозаменяемости

Звено	Номинальный размер	i2	Поле допуска	Квалитет	Допуск	В	Н	С
мм	мкм
АD	0,05	-				+100		+50
		3,46	±IT/2			+37	-37
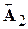
		2,42	h				-62	-37
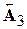
	9,95	0,81				-1	-37	-19

 

Можно, также рассчитать действительный коэффициент риска t по формуле:

.

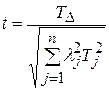По найденной величине t определим истинный процент брака и сравним с допустимым, в случае если он меньше или равен допустимому, то можно оставить полученные допуска составляющих звеньев. Если истинный процент брака превышает допустимый, необходимо ужесточить часть допусков и снова пересчитать истинный процент брака, пока он не будет равен или меньше, чем допустимый.