Потенціальні діаграми.

Потенціал чисельно дорівнює роботі по перенесенню одиничного додат-ного заряду із даної точки в точку фіксовану. Поверхня Землі, як провідника, еквіпотенціальна, потенціал її зручно прийняти нульовим. Тому й поняття «заземлити» означає прийняти потенціал даної точки за нуль. Потенціал будь-якої точки в електричному колі можна прийняти за нульовий, потенціали всіх інших точок відповідно зміняться, але різниця потенціалів точок залишиться без зміни.

Напруга між двома точками дорівнює різниці потенціалів цих точок. Це легко довести, виходячи з того, що робота по перенесенню заряду уздовж замк-неного шляху в потенціальному електричному полі дорівнює нулю. Тобто на-пруга між двома точками не залежить від шляху, а залежить лише від поло-ження цих точок.

На Рис. 21, а показана ідеальна ЕРС Еі опір R(Рис. 21, б), по якому проті-кає струмI. Приймемо, що потенціал точки б дорівнює нулю, «заземлимо» цю точку, 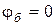. Потенціал точки а вищий потенціалу точки б на значення ЕРС Е, 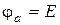. Напруга 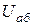між точками а, б: .

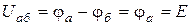Тобто, якщо проходити через ЕРС від «-» до «+» то потенціал зростає на величину ЕРС, напруга буде додатня у випадку проходження через ЕРС у напрямку від «+» до «-» ( проти вістря стрілки ).

Такі ж міркування застосуємо для опору зі струмом (Рис. 21,б). Приймемо потенціал точки б рівним нулю, 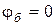. Очевидно, що струм тече від точки з вищим потенціалом до точки з нижчим потенціалом, аналогічно, як і вода те-че від верхнього рівня до нижнього. Тому потенціал точки а вищий від по-тенціалу точки бна величину падіння напруги IRна опоріR, 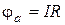. Напруга між точками а, б: .

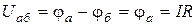Висновок:на ділянці з опором Rпотенціал зростає на IRу напрямку проти струму, а напруга додатня у напрямку, співпадаючому зі струмом.

Очевидно, для розглянутих випадків напруга між точками б, а 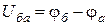буде від’ємна.

На Рис. 22 показана частина електричного кола, з ЕРС (джерелами напру-ги) та опорами, між точками а, б, по якій протікає струм І.

Знайдемо потенціал точки а відносно потенціалу точки б, тобто напругу між точками а і б:

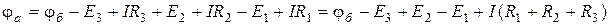
або ; звідки:

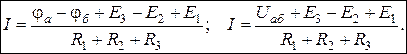
Це запис закону Ома , де струм вітки між полюсами а, б виражається за на-пругою між полюсами і параметрами вітки.

Для визначення струму у вітці за законом Ома при відомих параметрах по-трібно:

1) задатись довільним напрямком струму у вітці, наприклад, від точки а до точкиб,

2) в чисельнику записати напругу 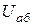(а не 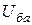); ЕРС, напрям яких спів-падає із вибраним напрямом струму, записати зі знаком «+», у проти-лежному разі - зі знаком «-»,

3) в знаменнику записати суму опорів вітки.

4) якщо в результаті розрахунків струм буде від’ємним, це означає, що на-прям руху додатніх зарядів протилежний вибраному.

У загальному вигляді закон Ома записується так:

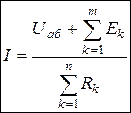
Закон Ома для замкненого нерозгалуженого кола: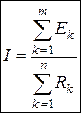

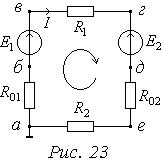
Розглянемо нерозгалужене коло (Рис. 23), в якому діють дві ЕРС, нехайЕ1> Е2. Тоді згідно із законом Ома:

струм буде співпадати з напрямком Е1. Приймемо поте-нціал точки аза нульовий і визначимо потенціали інших точок кола відносно нього.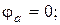

 

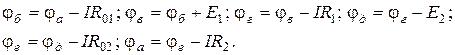
Розподіл потенціалів вздовж контура зручно зображати потенціальною діа-грамою (Рис. 24).

По вертикальній осі відкла-даються потенціали точок, по горизонтальній - сума опорів у тому порядку, якому вони роз-міщені в контурі.

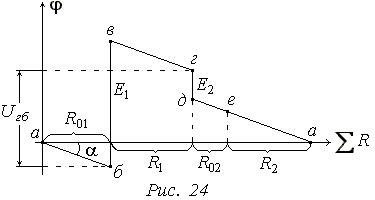Із діаграми можна визначити :

1) Напрям і значення струму в резисторі;Оскільки в даному контурі протікає один струм, то відрізкиIR діаграми мають однаковий кут нахилу. Тангенс кута нахилу відрізка, що зображає зміну потенціалу на резисторі, пропор-ційний струму на резисторі .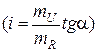

2) Напругу між будь-якими точками кола;на діаграмі показана напруга U_гб між точками г, б.