Структура електричного кола.

Кожен елемент електричного кола має, як мінімум, два зовнішні полюси, за допомогою яких він з’єднується з іншими елементами. Електричне коло утво-рюється об’єднанням полюсів елементів, які входять до його складу.

Аналіз електричного кола зводиться до визначення струмів і напруг всіх його елементів, якщо відомі параметри і спосіб з’єднання елементів між собою (структура, топологія).

З метою зменшення в розрахункових рівняннях кількості струмів і напруг для опису структури (топології) кола вводяться поняття : вітка і вузол.

Вітка – частина кола, яка розглядається відносно двох зовнішніх полюсів і характеризується струмом і напругою між цими полюсами. До складу вітки може входити один, або більша кількість елементів.

Основна вимога до внутрішньої структури вітки: повинна бути відомою, або легко знаходитись залежність між струмом і напругою на її зовнішніх полюсах. Найчастіше вітку утворюють декілька послідовно, або паралельно з’єднаних елементів.

Вузол – точка, в якій з’єднуються вітки між собою.

Отже, надалі будемо вважати, що задача аналізу електричного кола полягає в знаходженні струмів і напруг всіх його віток.

Структуру (топологію) електричного кола будемо розуміти як спосіб з’єд-нання між собою його віток. Дуже зручно показувати топологію кола у вигляді геометричної фігури – графа, який складається з ребер, що зображають вітки, і вершин, які зображають вузли кола.

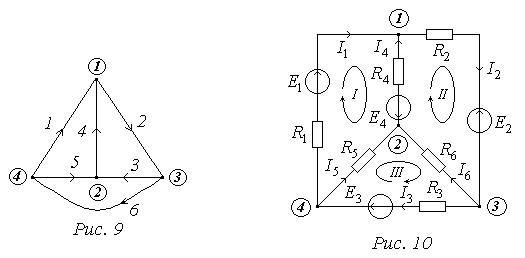
На Рис. 9 зображений орієнтований граф для кола (Рис. 10). Стрілками на кожному ребрі показують напрям струму вітки і одночасно напрям відрахунку напруги цієї вітки.

Вітки, як і вузли, нумеруються натуральними числами. Граф називається

планарним, якщо його можна розмістити на площині без перетину віток.

Структурні елементи графа:

1. Шлях – сукупність віток, які з’єднують початковий і кінцевий вузли. Якщо між двома будь-якими вузлами графа існує шлях, то граф назива-ється зв’язаним, інакше не зв’язаним.

2. Контур – замкнений шлях, в якому початковий і кінцевий вузли спів-падають. Для планарного графа вводиться поняття простий, або еле-ментарний контур (вічко) – це контур, який не охоплює жодної вітки. Наприклад, на Рис. 9 прості контури утворюються вітками: 1-4-5, 2-3-4, 3-5-6.

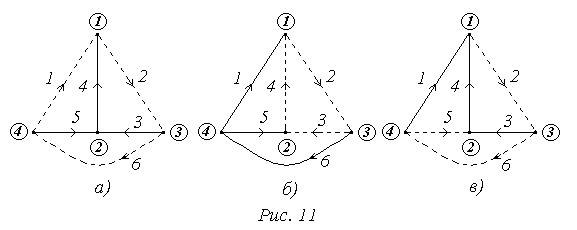
3. Дерево – сукупність віток, що з’єднують всі вузли, але не створюють жодного контура. На Рис. 11, а, б, в показані суцільними лініями три де-рева того ж самого графа. Очевидно, що кількість віток дерева у зв’я-заному графі на одиницю менша кількості вузлів: .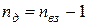

Всі вітки графа, які не належать дереву називаються вітками зв’язку, або інакше, хордами. На Рис. 11, а, б, в вони показані пунктиром.

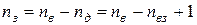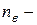Кількість віток зв’язку: , де загальна кількість віток графа.

4. Перетин – сукупність віток, при видаленні яких граф розпадається на дві, не зв’язані між собою частини. Наприклад, на Рис. 9 вітки 6, 5, 4, 2 утворюють перетин, тому що при їх видаленні граф розпадається на дві незв’язані частини: між вузлами 1, 4 залишається вітка 1, між вузлами 2, 3 – вітка 3.

5. Головний контур – контур, до складу якого входить лише одна вітка зв’язку, а всі інші – вітки дерева.

6. Головний перетин – перетин, до складу якого входить лише одна вітка дерева, а всі інші – вітки зв’язку.

Очевидно, що для кожного графа кількість головних контурів дорівнює кількості віток зв’язку, а кількість головних перетинів – кількості віток дерева.

Конкретні сукупності віток, що належать головним контурам і головним пе-ретинам, визначаються вибором дерева графа. Так, для дерева, показаного на Рис. 11, б головні контури утворені вітками: 2-1-6, 3-5-6, 4-1-5, головні перети-ни утворені вітками: 1-2-4, 5-3-4, 6-2-3. Проаналізуйте схеми кіл Рис. 11, а,в.

Струми і напруги у вітках підпорядковуються рівнянням, які поділяються на дві групи: топологічні і компонентні.

Топологічні рівняння визначаються топологією кола, тобто способом з’єд-нання віток між собою. Вони не залежать від внутрішньої структури віток і від того, які елементи входять до складу віток.

Спочатку розглянемо топологічні рівняння, які грунтуються на законах Кірхгофа для струмів і напруг.