На основе данных таможенной статистики
Одной из важнейших задач статистики является изучение изменений анализируемых показателей во времени, то есть их динамика. Эта задача решается при помощи анализа рядов динамики (временных рядов).
Ряд динамики – это числовые значения определенного статистического показателя в последовательные моменты или периоды времени (т.е. расположенные в хронологическом порядке).
Числовые значения того или иного статистического показателя, составляющего ряд динамики, называют уровнями ряда и обычно обозначают через y. Первый член ряда y1 называют начальным (базисным) уровнем, а последний yn – конечным. Моменты или периоды времени, к которым относятся уровни, обозначают через t.
Ряды динамики, как правило, представляют в виде таблицы (см. табл. 25) или графически (см. рис. 17), причем по оси абсцисс строится шкала времени t, а по оси ординат – шкала уровней ряда y.
Таблица 25. Внешнеторговый оборот (ВО) России за период 2000-2007 гг.
| Год | ||||||||
| Млрд. долл. США | 149,9 | 155,6 | 168,3 | 212,0 | 280,6 | 368,9 | 468,4 | 552,2 |
Рис. 17. Внешнеторговый оборот (ВО) России за период 2000-2007 гг.
Данные табл. 25 и рис. 17 наглядно иллюстрируют ежегодный рост внешнеторгового оборота (ВО) в России за период 2000-2007 гг.
Анализ рядов динамики начинается с определения того, как именно изменяются уровни ряда (увеличиваются, уменьшаются или остаются неизменными) в абсолютном и относительном выражении. Чтобы проследить за направлением и размером изменений уровней во времени, для рядов динамики рассчитывают показатели изменения уровней ряда динамики:
– абсолютное изменение (абсолютный прирост);
– относительное изменение (темп роста или индекс динамики);
– темп изменения (темп прироста).
Все эти показатели могут определяться базисным способом, когда уровень данного периода сравнивается с первым (базисным) периодом, либо цепным способом – когда сравниваются два уровня соседних периодов.
Абсолютное изменение (абсолютный прирост) уровней рассчитывается как разность между двумя уровнями ряда по формуле (69) – для базисного способа сравнения или по формуле (70) – для цепного. Оно показывает, на сколько (в единицах показателей ряда) уровень одного (i-го) периода больше или меньше уровня какого-либо предшествующего периода, и, следовательно, может иметь знак «+» (при увеличении уровней) или «–» (при уменьшении уровней).
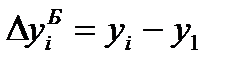 ; (69)
; (69) 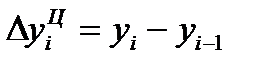 . (70)
. (70)
В табл. 26 в столбце 3 рассчитаны базисные абсолютные изменения по формуле (69), а в столбце 4 – цепные абсолютные изменения по формуле (70).
Таблица 26. Анализ динамики ВО России
| Год | y | 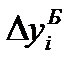
| 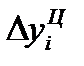
| 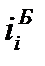
| 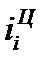
| 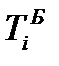 , % , %
| 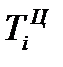 ,% ,%
|
| 149,9 | |||||||
| 155,6 | 5,7 | 5,7 | 1,038 | 1,038 | 3,8 | 3,8 | |
| 168,3 | 18,4 | 12,7 | 1,123 | 1,082 | 12,3 | 8,2 | |
| 62,1 | 43,7 | 1,414 | 1,260 | 41,4 | 26,0 | ||
| 280,6 | 130,7 | 68,6 | 1,872 | 1,324 | 87,2 | 32,4 | |
| 368,9 | 88,3 | 2,461 | 1,315 | 146,1 | 31,5 | ||
| 468,4 | 318,5 | 99,5 | 3,125 | 1,270 | 212,5 | 27,0 | |
| 552,2 | 402,3 | 83,8 | 3,684 | 1,179 | 268,4 | 17,9 | |
| Итого | 2355,9 | 402,3 | 3,684 |
Между базисными и цепными абсолютными изменениями существует взаимосвязь: сумма цепных абсолютных изменений равна последнему базисному изменению, т.е.
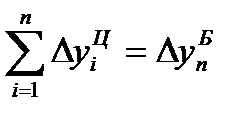 . (71)
. (71)
В нашем примере про ВО подтверждается правильность расчета абсолютных изменений по формуле (71): 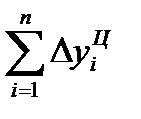 = 402,3 рассчитана в итоговой строке 4-го столбца, а
= 402,3 рассчитана в итоговой строке 4-го столбца, а 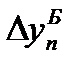 = 402,3 – в предпоследней строке 3-го столбца табл. 26.
= 402,3 – в предпоследней строке 3-го столбца табл. 26.
Относительное изменение (темп роста или индекс динамики) уровней рассчитывается как отношение (деление) двух уровней ряда по формуле (72) – для базисного способа сравнения или по формуле (73) – для цепного.
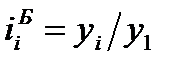 ; (72)
; (72) 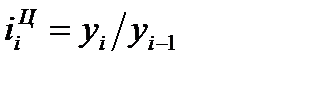 . (73)
. (73)
Относительное изменение показывает во сколько раз уровень данного периода больше уровня какого-либо предшествующего периода (при 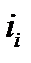 >1) или какую его часть составляет (при
>1) или какую его часть составляет (при 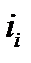 <1). Относительное изменение может выражаться в виде коэффициентов, то есть простого кратного отношения (если база сравнения принимается за единицу), и в процентах (если база сравнения принимается за 100 единиц) путем домножения относительного изменения на 100%.
<1). Относительное изменение может выражаться в виде коэффициентов, то есть простого кратного отношения (если база сравнения принимается за единицу), и в процентах (если база сравнения принимается за 100 единиц) путем домножения относительного изменения на 100%.
В табл. 26 в столбце 5 рассчитаны базисные относительные изменения по формуле (72), а в столбце 6 – цепные относительные изменения по формуле (73).
Между базисными и цепными относительными изменениями существует взаимосвязь: произведение цепных относительных изменений равно последнему базисному изменению, то есть
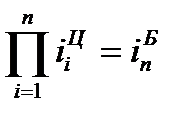 . (74)
. (74)
В нашем примере про ВО подтверждается правильность расчета относительных изменений по формуле (74): 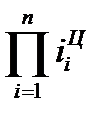 = 1,038*1,082*1,260*1,324*1,315*1,270*1,179 = 3,684 рассчитано по данным 6-го столбца, а
= 1,038*1,082*1,260*1,324*1,315*1,270*1,179 = 3,684 рассчитано по данным 6-го столбца, а 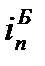 = 3,684 – в предпоследней строке 5-го столбца табл. 26.
= 3,684 – в предпоследней строке 5-го столбца табл. 26.
Темп изменения (темп прироста) уровней – относительный показатель, показывающий, на сколько процентов данный уровень больше (или меньше) другого, принимаемого за базу сравнения. Он рассчитывается путем вычитания из относительного изменения 100%, то есть по формуле (75):
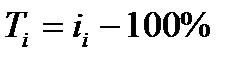 , (75)
, (75)
или как процентное отношение абсолютного изменения к тому уровню, по сравнению с которым рассчитано абсолютное изменение (базисный уровень), то есть по формуле (76):
 . (76)
. (76)
В табл. 26 в столбце 7 рассчитаны базисные темпы изменения ВО по формуле (75), а в столбце 8 – цепные темпы изменения по формуле (76). Все расчеты в табл. 26 свидетельствуют о ежегодном росте ВО России за период 2000-2007 гг.
Каждый ряд динамики можно рассматривать как некую совокупность n меняющихся во времени показателей, которые можно обобщить в виде средних величин. Такие обобщенные (средние) показатели особенно необходимы при сравнении динамики изменений того или иного показателя ВЭД в разные периоды, в разных странах и т.д.
Обобщенной характеристикой ряда динамики служит прежде всего средний уровень ряда 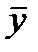 . Для разных видов рядов динамики он рассчитывается неодинаково. Ряды динамики бывают равномерные (с равными интервалами времени между уровнями), для которых средний уровень определяется по простой формуле средней величины, и неравномерные (с неравными интервалами), для которых используются формулы средних взвешенных (по интервалам времени) величин. В интервальном ряду динамики (в котором время задано в виде промежутков времени, к которым относятся уровни)
. Для разных видов рядов динамики он рассчитывается неодинаково. Ряды динамики бывают равномерные (с равными интервалами времени между уровнями), для которых средний уровень определяется по простой формуле средней величины, и неравномерные (с неравными интервалами), для которых используются формулы средних взвешенных (по интервалам времени) величин. В интервальном ряду динамики (в котором время задано в виде промежутков времени, к которым относятся уровни) 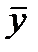 определяется по формуле средней арифметической, а в моментном ряду (в котором время задано в виде конкретных моментов времени или дат, к которым относятся уровни) – по формуле средней хронологической. В табл. 27 приводятся виды рядов динамики и соответствующие формулы для расчета их среднего уровня
определяется по формуле средней арифметической, а в моментном ряду (в котором время задано в виде конкретных моментов времени или дат, к которым относятся уровни) – по формуле средней хронологической. В табл. 27 приводятся виды рядов динамики и соответствующие формулы для расчета их среднего уровня 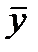 .
.
Таблица 27. Виды средних величин, применяемых при расчете среднего уровня
| Вид ряда динамики | Название средней величины | Формула средней величины | Номер формулы |
| Равномерный интервальный | Арифметическая простая | 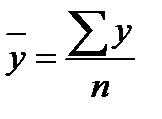
| (77) |
| Равномерный моментный | Хронологическая простая | 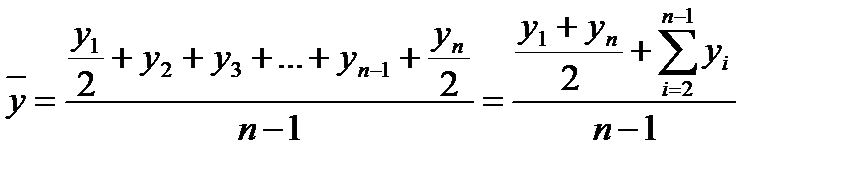
| (78) |
| Неравномерный интервальный | Арифметическая взвешенная | 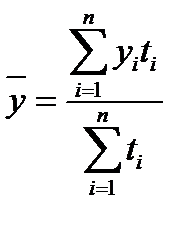
| (79) |
| Неравномерный моментный | Хронологическая взвешенная | 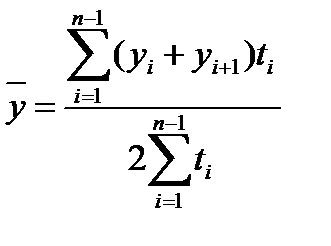
| (80) |
В нашем примере про ВО России за период 2000-2007 гг. имеем равномерный интервальный ряд динамики, поэтому его средний уровень определяем по формуле (77):  = 2355,9/8 = 294,488, то есть ВО России в период 2000-2007 гг. составлял ежегодно в среднем 294,488 млрд. долл. США.
= 2355,9/8 = 294,488, то есть ВО России в период 2000-2007 гг. составлял ежегодно в среднем 294,488 млрд. долл. США.
Кроме среднего уровня ряда рассчитываются и другие средние показатели:
– среднее абсолютное изменение (средний абсолютный прирост);
– среднее относительное изменение (средний темп роста);
– средний темп изменения (средний темп прироста).
Каждый из этих показателей может рассчитываться базисным и цепным способом.
Базисное среднее абсолютное изменение – это частное от деления последнего базисного абсолютного изменения на количество изменений уровней (81); цепное среднее абсолютное изменение уровней ряда – это частное от деления суммы всех цепных абсолютных изменений на количество изменений (82):
 Б =
Б = 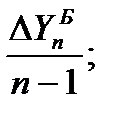 (81)
(81) 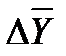 Ц =
Ц = 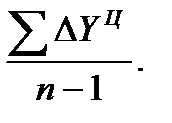 (82)
(82)
По знаку средних абсолютных изменений также судят о характере изменения явления в среднем: рост, спад или стабильность. Очевидно, что числители формулы (81) и (82) равны между собой по формуле (71), значит, среднее абсолютное изменение не зависит от способа расчета (базисный или цепной), так как результат получится одинаковый. В нашей задаче по формуле (81) или (82):
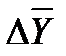 = 402,3/7 = 57,471, то есть ежегодно в среднем ВО растет на 57,471 млрд. долл.
= 402,3/7 = 57,471, то есть ежегодно в среднем ВО растет на 57,471 млрд. долл.
Наряду со средним абсолютным изменением рассчитывается и среднее относительное. Базисное среднее относительное изменение определяется по формуле (83), а цепное среднее относительное изменение – по формуле (84):
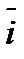 Б=
Б= 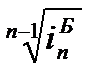 =
= 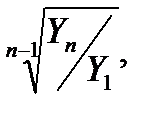 (83)
(83) 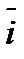 Ц=
Ц= 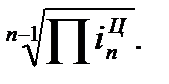 (84)
(84)
Естественно, базисное и цепное среднее относительное изменения должны быть одинаковыми и сравнением их с критериальным значением 1 делается вывод о характере изменения явления в среднем: рост, спад или стабильность. В нашем примере про ВО: 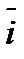 =
= 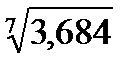 = 1,205, то есть ежегодно в среднем в период 2000-2007 гг. ВО России растет в 1,205 раза.
= 1,205, то есть ежегодно в среднем в период 2000-2007 гг. ВО России растет в 1,205 раза.
Вычитанием 100% из среднего относительного изменения образуется соответствующий средний темп изменения, по знаку которого также можно судить о характере изменения изучаемого явления, отраженного данным рядом динамики. В нашем примере про ВО: 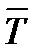 = 1,205 – 1 = 0,205, то есть ежегодно в среднем в период 2000-2007 гг. ВО России растет на 20,5%.
= 1,205 – 1 = 0,205, то есть ежегодно в среднем в период 2000-2007 гг. ВО России растет на 20,5%.
Одна из основных задач изучения рядов динамики – выявить основную тенденцию (закономерность) в изменении уровней ряда, именуемую трендом. Закономерность в изменении уровней ряда в одних случаях проявляется наглядно, в других – может маскироваться колебаниями случайного или неслучайного характера. Поэтому, чтобы сделать правильные выводы о закономерностях развития того или иного показателя, надо суметь отделить тренд от колебаний, вызванных случайными кратковременными причинами. На основании выделенного тренда можно экстраполировать (прогнозировать) развитие явления в будущем. С этой целью (устранить колебания, вызванные случайными причинами) ряды динамики подвергают обработке.
Существует несколько методов обработки рядов динамики, помогающих выявить основную тенденцию изменения уровней ряда, а именно: метод укрупнения интервалов, метод скользящей средней и аналитическое выравнивание. Во всех методах вместо фактических уровней при обработке ряда рассчитываются иные (расчетные) уровни, в которых тем или иным способом взаимопогашается действие случайных факторов и тем самым уменьшается колеблемость уровней. Последние в результате становятся как бы «выравненными», «сглаженными» по отношению к исходным фактическим данным. Такие методы обработки рядов динамики называются сглаживанием или выравниванием рядов динамики.
Наиболее совершенным методом обработки рядов динамики в целях устранения случайных колебаний и выявления тренда является выравнивание уровней ряда по аналитическим формулам (или аналитическое выравнивание). Суть аналитического выравнивания заключается в замене эмпирических (фактических, исходных) уровней yi теоретическими 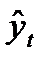 , которые рассчитаны по определенному уравнению, принятому за математическую модель тренда, где теоретические уровни рассматриваются как функция времени:
, которые рассчитаны по определенному уравнению, принятому за математическую модель тренда, где теоретические уровни рассматриваются как функция времени: 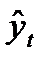 = f(t).
= f(t).
При этом каждый фактический уровень yi рассматривается как сумма двух[30] составляющих:
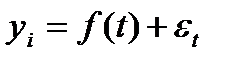 , (85)
, (85)
где f(t) = 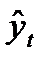 - систематическая составляющая, отражающая тренд и выраженная определенным уравнением;
- систематическая составляющая, отражающая тренд и выраженная определенным уравнением; 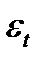 - случайная величина, вызывающая колебания уровней вокруг тренда.
- случайная величина, вызывающая колебания уровней вокруг тренда.
Задача аналитического выравнивания сводится к следующему:
1) определение на основе фактических данных формы (вида) гипотетической функции 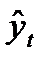 = f(t), способной наиболее адекватно отразить тенденцию развития исследуемого показателя;
= f(t), способной наиболее адекватно отразить тенденцию развития исследуемого показателя;
2) нахождение по эмпирическим данным параметров указанной функции;
3) расчет по найденному уравнению теоретических (выравненных) уровней.
В аналитическом выравнивании наиболее часто используются простейшие функции, представленные в табл. 28, где обозначено 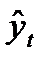 - теоретические (выравненные) уровни (читается как «игрек, выравненный по t»); t – условное обозначение времени (1, 2, 3 …); a0, a1, a2, ... – параметры аналитической функции; k – число гармоник (при выравнивании по ряду Фурье).
- теоретические (выравненные) уровни (читается как «игрек, выравненный по t»); t – условное обозначение времени (1, 2, 3 …); a0, a1, a2, ... – параметры аналитической функции; k – число гармоник (при выравнивании по ряду Фурье).
Таблица 28. Виды математических функций[31], используемые при выравнивании
| Название функции | График функции | Формула |
| Прямая линия |  (86) (86)
| |
| Парабола 2-го порядка | или | 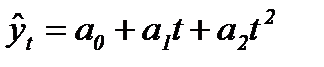 (87) (87)
|
| Гипербола | 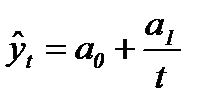 (88) (88)
| |
| Показательная | 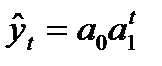 (89) (89)
| |
| Степенная | 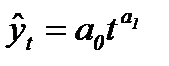 (90) (90)
| |
| Ряд Фурье | 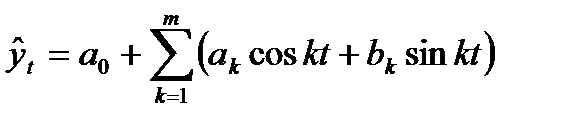 (91) (91)
|
Выбор той или иной функции для выравнивания ряда динамики осуществляется на основании графического изображения эмпирических данных. Если по тем или иным причинам уровни эмпирического ряда трудно описать одной функцией, следует разбить анализируемый период на отдельные части и затем выровнять каждую часть по соответствующей кривой.
Нередко один и тот же ряд можно выровнять по разным аналитическим функциям и получить довольно близкие результаты. В нашем примере про ВО России можно произвести выравнивание и по прямой линии, и по параболе. Чтобы решить вопрос о том, использование какой кривой дает лучший результат, обычно сопоставляют суммы квадратов отклонений эмпирических уровней от теоретических (остатки), рассчитанным по разным функциям, то есть:
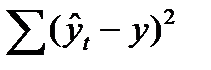 . (92)
. (92)
Та функция, при которой эта сумма минимальна, считается наиболее адекватной, приемлемой. Однако сравнивать непосредственно суммы квадратов отклонений можно в том случае, если сравниваемые уравнения имеют одинаковое число параметров. Если же число параметров k разное, то каждую сумму квадратов делят на разность (n – k), выступающую в роли числа степеней свободы, и сравнивают уже квадраты отклонений уровней, рассчитанные на одну степень свободы (т.е. остаточные дисперсии на одну степень свободы).
Параметры искомых уравнений (a0, a1, a2, ...) при аналитическом выравнивании могут быть определены по-разному, но наиболее распространенным методом является метод наименьших квадратов (МНК). При этом методе учитываются все эмпирические уровни и должна обеспечиваться минимальная сумма квадратов отклонений эмпирических значений уровней y от теоретических уровней 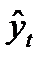 :
:
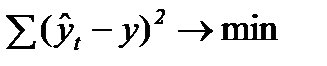 . (93)
. (93)
В частности, при выравнивании по прямой вида (86) параметры 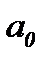 и
и  отыскиваются по МНК следующим образом. В формуле (93) вместо
отыскиваются по МНК следующим образом. В формуле (93) вместо 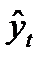 записываем его конкретное выражение
записываем его конкретное выражение  . Тогда
. Тогда 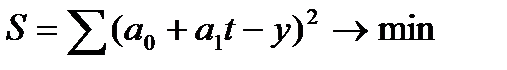 . Дальнейшее решение сводится к задаче на экстремум, т.е. к определению того, при каком значении
. Дальнейшее решение сводится к задаче на экстремум, т.е. к определению того, при каком значении 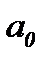 и
и 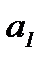 функция двух переменных S может достигнуть минимума. Как известно, для этого надо найти частные производные S по
функция двух переменных S может достигнуть минимума. Как известно, для этого надо найти частные производные S по 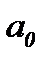 и
и  , приравнять их к нулю и после элементарных преобразований решить систему двух уравнений с двумя неизвестными.
, приравнять их к нулю и после элементарных преобразований решить систему двух уравнений с двумя неизвестными.
В соответствии с вышеизложенным найдем частные производные:
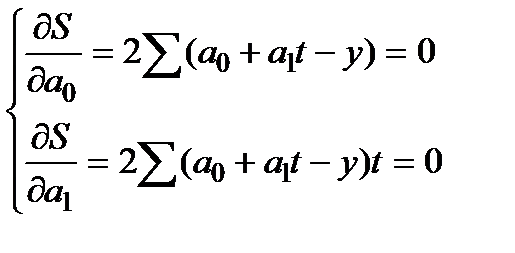
Сократив каждое уравнение на 2, раскрыв скобки и перенеся члены с y в правую сторону, а остальные – оставив в левой, получим систему нормальных уравнений:
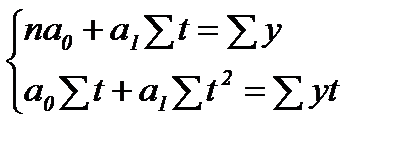 (94)
(94)
где n – количество уровней ряда; t – порядковый номер в условном обозначении периода или момента времени; y – уровни эмпирического ряда.
Эта система и, соответственно, расчет параметров 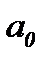 и
и  упрощаются, если отсчет времени ведется от середины ряда[32]. Например, при нечетном числе уровней серединная точка времени (год, месяц) принимается за нуль, тогда предшествующие периоды обозначаются соответственно –1, –2, –3 и т.д., а следующие за средним (центральным) – соответственно 1, 2, 3 и т.д. При четном числе уровней (как в нашем примере про ВО России – 7 уровней) два серединных момента (периода) времени обозначают –1 и +1, а все последующие и предыдущие, соответственно, через два интервала:
упрощаются, если отсчет времени ведется от середины ряда[32]. Например, при нечетном числе уровней серединная точка времени (год, месяц) принимается за нуль, тогда предшествующие периоды обозначаются соответственно –1, –2, –3 и т.д., а следующие за средним (центральным) – соответственно 1, 2, 3 и т.д. При четном числе уровней (как в нашем примере про ВО России – 7 уровней) два серединных момента (периода) времени обозначают –1 и +1, а все последующие и предыдущие, соответственно, через два интервала: 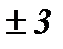 ,
, 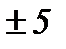 ,
,  и т.д. (см. 3-й столбец табл. 29).
и т.д. (см. 3-й столбец табл. 29).
При таком порядке отсчета времени (от середины ряда) 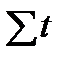 = 0, поэтому, система нормальных уравнений (94) упрощается до следующих двух уравнений, каждое из которых решается самостоятельно:
= 0, поэтому, система нормальных уравнений (94) упрощается до следующих двух уравнений, каждое из которых решается самостоятельно:
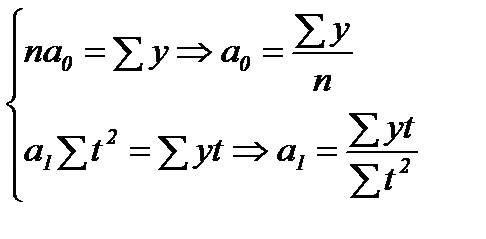 (95)
(95)
Как видим, при такой нумерации периодов параметр a0 представляет собой средний уровень равномерного интервального ряда, то есть формулу (77). Определим по формуле (95) параметры уравнения прямой для нашего примера про ВО России, для чего исходные данные и все расчеты необходимых сумм представим в табл. 29.
Таблица 29. Вспомогательные расчеты для линейного тренда
| Год | y | t | t2 | yt | 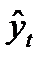
| 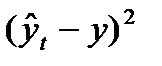
| 
| 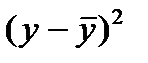
|
| 149,9 | -7 | -1049,3 | 84,050 | 4336,223 | 44283,941 | 20905,545 | ||
| 155,6 | -5 | -778 | 144,175 | 130,531 | 22593,848 | 19289,738 | ||
| 168,3 | -3 | -504,9 | 204,300 | 1296,000 | 8133,785 | 15923,285 | ||
| -1 | -212 | 264,425 | 2748,381 | 903,754 | 6804,188 | |||
| 280,6 | 280,6 | 324,550 | 1931,602 | 903,754 | 192,863 | |||
| 368,9 | 1106,7 | 384,675 | 248,851 | 8133,785 | 5537,220 | |||
| 468,4 | 444,800 | 556,960 | 22593,848 | 30245,558 | ||||
| 552,2 | 3865,4 | 504,925 | 2234,926 | 44283,941 | 66415,733 | |||
| Итого | 2355,9 | 5050,5 | 2355,900 | 13483,473 | 151830,656 | 165314,129 |
Из табл. 29 получаем, что: a0 = 2355,9/8 = 294,4875 и a1 = 5050,5/168 = 30,0625. Отсюда искомое уравнение тренда: 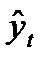 =294,4875+30,0625t. В 6-м столбце табл. 29 приведены теоретические (трендовые) уровни, рассчитанные по этому уравнению, а в итоге 7-го столбца – остатки по формуле (92). Для иллюстрации построим график эмпирических и трендовых уровней – рис. 18.
=294,4875+30,0625t. В 6-м столбце табл. 29 приведены теоретические (трендовые) уровни, рассчитанные по этому уравнению, а в итоге 7-го столбца – остатки по формуле (92). Для иллюстрации построим график эмпирических и трендовых уровней – рис. 18.
Рис. 18. Эмпирические и трендовые уровни ряда динамики ВО России
Для найденного уравнения тренда необходимо провести оценку его надежности (адекватности), что осуществляется обычно с помощью критерия Фишера, сравнивая его расчетное значение Fр с теоретическим (табличным) значением FТ (Приложение 8). При этом расчетный критерий Фишера определяется по формуле (96):
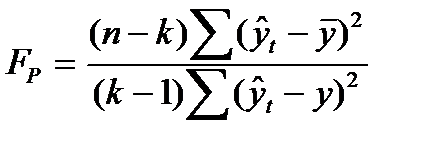 , (96)
, (96)
где k – число параметров (членов) выбранного уравнения тренда.
Для проверки правильности расчета сумм в формуле (96) можно использовать следующее равенство (97):
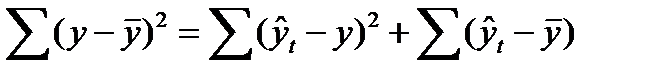 . (97)
. (97)
В нашем примере про ВО равенство (97) соблюдается (необходимые суммы рассчитаны в трех последних столбцах табл. 29): 165314,129 = 13483,473 + 151830,656.
Сравнение расчетного и теоретического значений критерия Фишера ведется при заданном уровне значимости[33]с учетом степеней свободы:  и
и 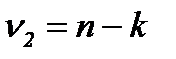 . При условии Fр > FТ считается, что выбранная математическая модель ряда динамики адекватно отражает обнаруженный в нем тренд.
. При условии Fр > FТ считается, что выбранная математическая модель ряда динамики адекватно отражает обнаруженный в нем тренд.
Проверим тренд на адекватность в нашем примере про ВО по формуле (96):
FР = 151830,656*6/(13483,473*1) = 67,563 > FТ, значит, модель адекватна и ее можно использовать для прогнозирования (FТ = 5,99 находим по Приложению 8 в 1-ом столбце [ 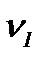 = k – 1 = 2 – 1 = 1] и 5-й строке [
= k – 1 = 2 – 1 = 1] и 5-й строке [ 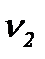 = n – k = 6]).
= n – k = 6]).
Как уже было отмечено ранее, в нашем примере про ВО России можно произвести выравнивание не только по прямой линии, но и по параболе, чего делать не будем, так как уже найденный линейный тренд адекватно описывает тенденцию[34].
При составлении прогнозов уровней социально-экономических явлений обычно оперируют не точечной, а интервальной оценкой, рассчитывая так называемые доверительные интервалы прогноза. Границы интервалов определяются по формуле (98):
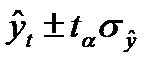 , (98)
, (98)
где 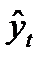 – точечный прогноз, рассчитанный по модели тренда;
– точечный прогноз, рассчитанный по модели тренда; 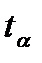 – коэффициент доверия по распределению Стьюдента при уровне значимости
– коэффициент доверия по распределению Стьюдента при уровне значимости 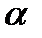 и числе степеней свободы
и числе степеней свободы 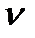 =n–1 (приложение 9)[35];
=n–1 (приложение 9)[35]; 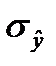 – ошибка аппроксимации, определяемая по формуле (99):
– ошибка аппроксимации, определяемая по формуле (99):
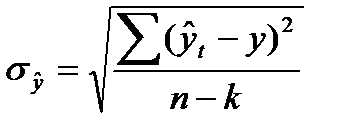 . (99)
. (99)
Спрогнозируем ВО России на 2008 и 2009 годы с вероятностью 0,95 (значимостью 0,05), для чего найдем ошибку аппроксимации по формуле (99): 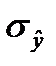 =
= 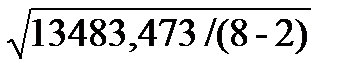 = 47,405 и найдем коэффициент доверия по распределению Стьюдента по Приложению 9:
= 47,405 и найдем коэффициент доверия по распределению Стьюдента по Приложению 9: 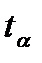 = 2,3646 при
= 2,3646 при 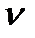 = 8 – 1= 7.
= 8 – 1= 7.
Прогноз на 2008 и 2009 годы с вероятностью 0,95 по формуле (98):
Y2008 = (294,4875+30,0625*9) 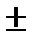 2,3646*47,405 или 452,96<Y2008<677,14 (млрд. долл.);
2,3646*47,405 или 452,96<Y2008<677,14 (млрд. долл.);
Y2009 = (294,4875+30,0625*11) 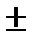 2,3646*47,405 или 513,08<Y2009<737,27 (млрд. долл.).
2,3646*47,405 или 513,08<Y2009<737,27 (млрд. долл.).
Как видно из полученных прогнозов, доверительный интервал достаточно широк (из-за достаточно большой величины ошибки аппроксимации). Более точный прогноз можно получить при выравнивании по параболе 2-го порядка[36].
Дата добавления: 2015-02-13; просмотров: 1154;
