Введение. Рассмотрим последовательно сопряжение двух прямых, прямой и дуги и двух дуг при заданном радиусе R.

Рассмотрим последовательно сопряжение двух прямых, прямой и дуги и двух дуг при заданном радиусе R.

Для построения сопряжения двух пересекающихся прямых l₁иl₂ нарасстоянии заданного радиуса R проводим две вспомогательные прямые, соответственно параллельные заданным l₁ и l₂ (рисунок 32). Точка пересечения этих прямых является центром сопряжения О. Из полученного центра опускаем перпендикуляры на заданные прямые - получаем точки сопряжений М и N. Из центра О величиной заданного радиуса R проводим дугу в пределах между найденными точками М и N.

Для построения сопряжения прямой линии l с дугой радиуса R₁ , проведенной из центра O₁ (рисунок 33), проводим вспомогательную прямую, параллельную прямой l, на расстоянии заданного радиуса сопряжения R, а из центра O₁ проводим вспомогательную дугу радиусом R₁+R. В точке пересечения этих вспомогательных линий получаем центр сопряжения О. Из этого центра опускаем перпендикуляр на прямую - получаем точку сопряжения на прямой М, затем соединяем центр О с центром дуги O₁ - в пересечении прямой ОО₁ с заданной дугой получаем точку сопряжения на дуге - точкуN. Между найденными точками М и N радиусом R проводим дугу сопряжения.

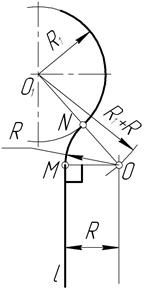
Рисунок 32 Рисунок 33

Для построения сопряжения двух дуг: дуги R₁ из центра O₁ и дуги R₂ из центра O₂ (рисунок 34), проводим две вспомогательные дуги радиусами, соответственно равными R₁+R и R₂+R. Точка пересечения вспомогательных дуг определяет центр сопряжения - точку О. Для определения точек сопряжения М и N соединяем центр сопряжения О с центрами заданных дуг O₁ и O₂. Радиусом R проводим дугу сопряжения в пределах MN.

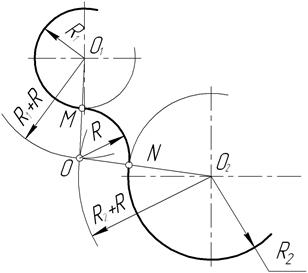
Рисунок 34

Сопряжение двух дуг при заданном радиусе R возможно при следующем условии: O₁ O₂ ≤ R₁ + 2R + R₂

Рассмотрев наиболее характерные случаи сопряжений при заданном радиусе, можно выявить общее правило построения сопряжений для подобных случаев. Центр сопряжения определяется в пересечении двух вспомогательных линий, параллельных заданным дугам и отстоящих от заданных линий на расстоянии радиуса сопряжения.

Точки сопряжений определяются: на прямых - перпендикуляром, опущенным из центра сопряжений на прямую; на дугах - прямой, соединяющей центр сопряжений с центром заданной дуги (рисунки 32 – 34).

7.2.2 Задана точка сопряжения

Рассмотрим несколько характерных случаев сопряжения двух прямых, прямой и дуги и двух дуг, когда задана одна точка сопряжения М.

Для построения сопряжения двух пересекающихся прямых l₁ и l₂ (рисунок 35) центр сопряжения О определяем в точке пересечения перпендикуляра к прямой l₁ , восставленного из заданной точки М, и биссектрисы угла, образованного прямыми l₁ и l₂. Вторую точку сопряжения N на прямой l₂ определяем с помощью перпендикуляра, опущенного из центра O на прямую l₂. Радиус сопряжения определяем графически: R_X = |ОМ|= |ON|.

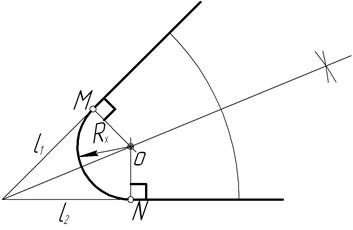
Рисунок 35

Построение сопряжения прямой линии l c дугой радиуса R₁, проведенной из центра O₁. Эта задача может быть решена в двух вариантах, точка М может быть задана на дуге и на прямой. Рассмотрим последовательно оба варианта.

Первый вариант. Точка М задана на дуге. В точке М проводим касательную к дуге. Точка пересечения биссектрисы угла, образованного касательной и заданной прямой l, с продолжением радиуса O₁М определяем центр дуги сопряжения О (рисунок 36).

Вторая точка сопряжения N на прямой определяется перпендикуляром, опущенным из точки О на прямую l. Радиус сопряжения определился графически: R_X = |ОМ|= |ON|.

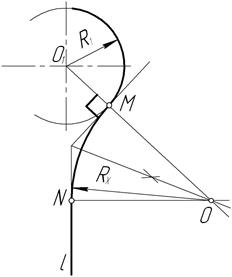
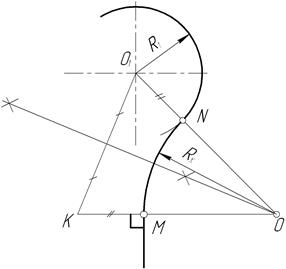
Рисунок 36 Рисунок 37

Второй вариант. Точка М задана на прямой. Из заданной точки М восстанавливаем перпендикуляр к прямой l и откладываем на нем расстояние, равное R₁ (рисунок 37). Полученную точку К соединяем с центром O₁ и делим отрезок O₁ К пополам. Центр дуги сопряжения O определяется в точке пересечения перпендикуляра, восстановленного из середины отрезка O₁ К и прямой, проходящей через точки М и К.

Вторую точку сопряжения N на дуге определяем в точке пересечения прямой OO₁ c заданной дугой. Радиус сопряжения R_X = |ОМ| = |ON|.

Построить сопряжение двух дуг R₁ из центра O₁и R₂ из центра O₂. Точка сопряжения М задана на дуге, проведенной из центра O₁. Соединяем заданную точку М с центром O₁ и откладываем на продолжении радиуса O₁ М расстояние, равное R₂ (рисунок 38). Дальнейшее построение аналогично предыдущему случаю; полученную точку К соединяем с центром O₂ и делим отрезок КO₂ пополам. Центр дуги сопряжения О определяется в точке пересечения перпендикуляра, восстановленного от середины отрезка КO₂, и прямой, проходящей через точки M и O₁. Вторую точку сопряжения на второй дуге определяем в точке пересечения дуги с прямой OO₂. Радиус сопряжения R_X = |ОМ|= |ON|.

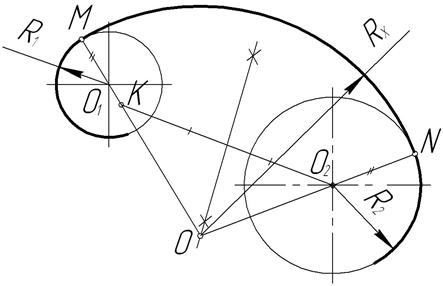
Рисунок 38

При обводке сопряженных линий сначала следует обводить дуги до точек сопряжений, а затем прямолинейные участки.

7.3 Лекальные кривые

Лекальные кривые имеют большое применение в технике. Рассмотрим наиболее часто встречающиеся способы построения плоских кривых: эллипса, параболы, циклоиды, синусоиды, эвольвенты. Это кривые обычно обводят с помощью лекал, поэтому они получили название лекальных кривых.

Эллипс (рисунок 39). Эллипсом называется замкнутая плоская кривая, для которой сумма расстояний от любой ее точки до двух точек той же плоскости - фокусов эллипса - есть величина постоянная, равная большой оси эллипса. Отрезок MN называется большой осью эллипса, а отрезок DE - малой его осью. Если из точки D или Е провести дугу радиусом R=MN:2, то на большой оси эллипса будут получены его фокусы (точки F₁ и F₂).

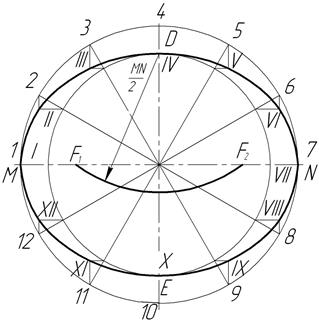
Рисунок 39

Для построения эллипса проводят две концентрические окружности, диаметры которых равны осям эллипса. Эти окружности делят на несколько частей (12…16). Через точки деления на большой окружности проводят вертикальные линии, через соответствующие точки деления на малой окружности - горизонтальные линии. Пересечение этих линий даст точки эллипса I, II, III... (другие способы построения эллипса см. в рекомендуемой литературе).

Рекомендуется при обводке эллипса и других симметричных кривых делать на лекале засечки-черточки карандашом и прикладывать этот участок, лекала к симметричной части кривой.

Парабола (рисунок 40). Параболой называется плоская кривая, каждая точка которой расположена на одинаковом расстоянии от заданной прямой, носящей название директрисы, и точки, называемой фокусом параболы, расположенных в той же плоскости.

Рассмотрим один из способов построения параболы. Даны: вершина параболы О, одна из точек параболы D и направление оси ОС. На отрезках ОС и CD строят прямоугольник, стороны этого прямоугольника ОВ и BD делят на произвольное одинаковое число равных частей и нумеруют точки деления. Вершину О соединяют с точками деления BD, а из точек деления отрезка ОВ проводят прямые, параллельные оси. Пересечение прямых, проходящих через точки с одинаковыми номерами, определяет ряд точек параболы (другие способы построения параболы см. в рекомендуемой литературе).

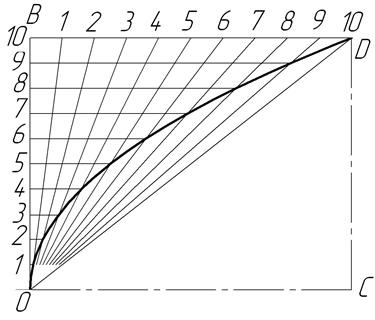
Рисунок 40

Циклоида (рисунок 41). Траектория точки А, принадлежащей окружности, перекатываемой без скольжения по прямой, называется циклоидой. Для ее построения от исходного положения точки A на направляющей прямой откладывают отрезок АA₁ , равный длине данной окружности 2πR. Окружность и отрезок АA₁ делят на одинаковое число равных частей. Восстанавливая перпендикуляры из точек деления прямой АA₁ до пересечения с прямой, проходящей через центр данной окружности параллельно АA₁ , намечают ряд последовательных положений центра перекатываемой окружности O₁ , O₂ , O₃ , …, O₈. Описывая из этих центров окружности радиуса R, отмечают точки пересечения с ними прямых, проходящих параллельно АA₁ , через точки деления окружности 1,2, 3 и т. д.

В пересечении горизонтальной прямой, проходящей через точку 1, с окружностью, описанной из центра O₁ , находится одна из точек циклоиды; в пересечении прямой, проходящей через точку 2, с окружностью, проведенной из центра О₂ , находится другая точка циклоиды и т. д. Соединяя полученные точки плавной кривой, получаем циклоиду.

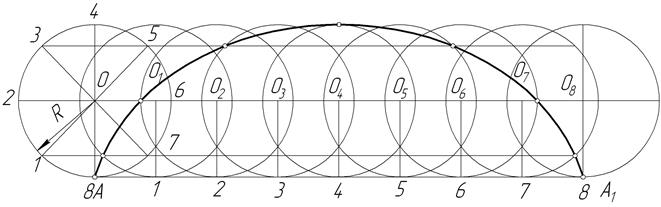
Рисунок 41

Синусоида (рисунок 42). Для построения синусоиды делят окружность заданного радиуса на равные части (6, 8, 12 и т. д.) и на продолжении осевой линии от условного начала - точки А - проводят отрезок прямой AB, равный 2πR. Затем прямую делят на такое же число равных частей, как и окружность (6, 8, 12 и т. д.). Из точек окружности 1, 2, 3, ... , 12 проводят прямые линии параллельно выбранной прямой до пересечения с соответствующими перпендикулярами, восстановленными или опущенными из точек деления прямой. Полученные точки пересечения (1', 2', 3', ... , 12') будут точками синусоиды с периодом колебания, равным 2πR. Точки 3' и 9' кривой являются вершинами точки А, 6 и В - точками перегиба.

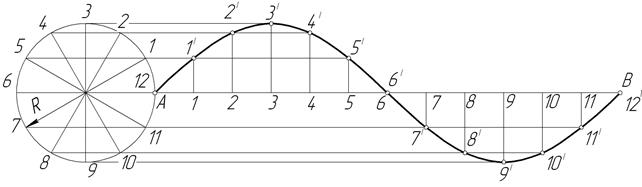
Рисунок 42

Эвольвента (развертка окружности, рисунок 43). Эвольвентой называется траектория, описываемая каждой точкой прямой линии, перекатываемой по окружности без скольжения. В машиностроении по эвольвенте очерчивают профиль зубьев зубчатых колес. Для построения эвольвенты окружность предварительно делят на произвольное число равных частей; в точках деления проводят касательные к окружности, направленные в одну сторону. На касательной, проведенной через последнюю точку деления, откладывают отрезок, равный длине окружности 2πR, и делят его на то же число n равных частей. Откладывая на первой касательной одно деление, равное πD/n, на второй - два, на третьей - три и т. д., получают ряд точек I, II, III и т. д., которые соединяют по лекалу.

Рисунок 43

Построение гиперболы, эпициклоиды, гипоциклоиды, спирали Архимеда, строфоиды и т. д. см. в рекомендуемой литературе.

Для обводки кривой по лекалу рекомендуется соединить полученные точки тонкой линией от руки на глаз, стараясь при этом придать кривой линии возможно более плавные очертания, и лишь после этого подобрать лекало, соответствующее кривизне того или иного ее участка (рисунок 44), соединяя не менее трех точек одновременно.

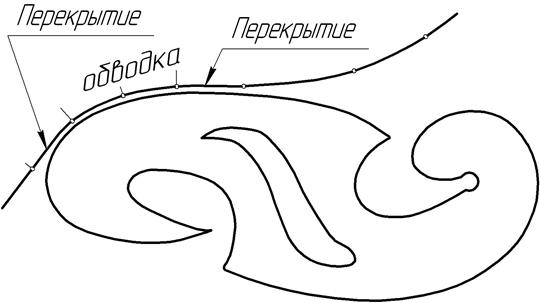
Рисунок 44

7.4 Сопряжения прямой с лекальными кривыми (касательные к лекальным кривым)

Ранее были рассмотрены различные случаи сопряжения прямых, прямой с дугой и двух дуг. На практике нередко встречается сопряжение прямой с лекальными кривыми, при этом сопрягаемая прямая должна быть направлена по касательной к кривой, проведенной через заданную точку сопряжения.

Рассмотрим примеры построения сопряжений прямой с эллипсом (рисунок 45). Задана точка сопряжения D. Касательная к эллипсу в данной точке проходит перпендикулярно биссектрисе угла, образованного прямыми F₁ D и F₂ D, где F₁ и F₂ - фокусы эллипса.

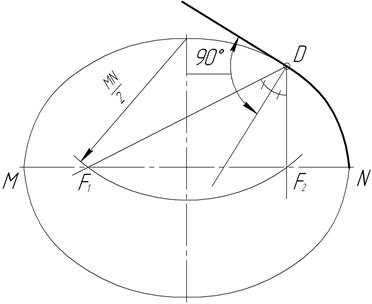
Рисунок 45

На рисунке 46 показано построение касательной к параболе в заданной точке М. Касательная соединяет заданную точку М с точкой К, положение которой определяется соотношением AK=AN. Способы построения касательных к другим заданным лекальным кривым можно изучить в рекомендуемой литературе.

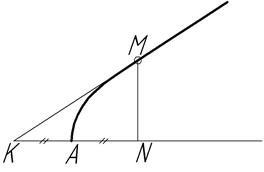
Рисунок 46

7.5 Вопросы для самопроверки

Вопросы для самопроверки к теме 1:

1. Сколько листов формата А4 содержится в листе формата А1?

2. Как образуются дополнительные форматы чертежей?

3. Чем определяется размер шрифта?

4. Чему равна высота строчных букв по сравнению с
прописными?

5. Допускается ли применение в чертежах прямого шрифта?

6. От чего зависит выбор толщины линии обводки видимого контура?

7. Какого начертания и какой толщины проводят линии осевые, центровые, выносные, размерные и невидимого контура?

8. Как проводят центровые линии окружности небольшого диаметра (менее 12 мм)?

9. В каких единицах проставляют размеры на чертежах?

10. На каком расстоянии от контура рекомендуется проводить размерные линии?

11. В каких случаях стрелку размерной линии заменяют точкой или штрихом?

12. Как располагают цифры размеров угла?

13. В каких случаях проставляют знак диаметра Æ?

14. Какие проставляют размеры при выполнении чертежа в масштабе, отличном от 1:1?

15. На каких двух положениях геометрии основано построение сопряжений?

16. Перечислите элементы сопряжений.

Введение

Изучение интенсивно развивающейся и наукоемкой предметной области, такой как микроэлектроника и микропроцессорная техника - задача интересная и сложная, требующая постоянного со-вершенствования, пополнения получаемых знаний и знакомства со смежными научно-техническими областями. В связи с широким применением электронных систем управления и с целью эффективного решения любых прикладных задач современный специалист, профессионально связанный и не связанный с вычислительной тех-никой, должен иметь не только элементарное представление об основных понятиях построения современных электронных систем, но и иметь адекватное представление о состоянии и перспективах раз-вития элементной базы.

Развитие компьютерной техники - наивысшего достижения электроники - последнее десятилетие шло такими шагами, что на сегодняшний день практически невозможно представить ни одну сферу жизни, где бы не применялись микропроцессоры (МП): от персональных компьютеров - до управления сложнейшими технологическими процессами, от управления бытовыми стиральными машинами и сотовыми телефонами - до проектирующих рабочих станций и многопроцессорных супер-ЭВМ.

За чуть более чем четверть вековую историю микропроцессоры прошли поистине гигантский путь.

Первая микросхема МП, выпущенная фирмой INTEL в 1971 г., работала на тактовой частоте 108 кГц, содержала 2300 транзисторов, выполнена была по 10 мкм технологии и стоила около 200 долларов. Одна из последних модификаций микросхемы INTEL PENTIUM-4 выполнена по 0,09 мкм технологии, имеет 140 миллионов транзисторов внутри кристалла полупроводника размером 87кв.мм.

Сравнение вышеприведенных данных подтверждает и образная оценка успехов микропроцессорной индустрии, данная основателем и председателем совета директоров фирмы INTEL Гордоном Муром (Gordon Moore): «Если бы автомобилестроение эволюционировало со скоростью полупроводникововой промышленности, то сегодня «Роллс-ройс» стоил бы 3 доллара, мог проехать полмиллиона миль на одном галлоне бензина, и было бы дешевле его выбросить, чем платить за парковку».

Не трудно понять, что и на сегодняшний день компьютеризация является одним из главных направлений научно-технического прогресса и концентрированным его выражением. В МП воплощены самые передовые достижения инженерной мысли, и от того, в какой степени насыщены вычислительной техникой самые различные отрасли производства, зависит не только экономический, но и военный потенциал страны.