Характеристика процессов системы

Процессы системы — это совокупность последовательных изменений состояния системы для достижения цели.

К процессам системы относятся:

входной процесс;

выходной процесс;

переходный процесс системы.

Входной процесс — множество входных воздействий, которые изменяются с течением времени.

Входной процесс можно задать, если каждому моменту времени t поставить в соответствие по определенному правилу со входные воздействия х с X. Моменты времени t определены на множестве Т, t Î Т. В результате этот входной процесс будет представлять собой функцию времени 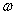: Т® Y [х].

Функции входных процессов — задание по определенному правилу, в определенные моменты времени управляющих воздействий.

Выходной процесс множество выходных воздействий на окружающую среду, которые изменяются с течением времени.

Воздействие системы на окружающую среду определяется выходными величинами (реакциями). Выходные величины изменяются с течением времени, образуя выходной процесс, представляющий функцию у: Т ® Y[X].

Функции выходных процессов — задание по определенному правилу, в определенные моменты времени выходных величин (реакций) системы.

Множество допустимых функций, характеризующих выходной процесс, обозначим Г = {y, T ® Y}. Для обозначения мгновенных значений выходных величин в моменты t можно использовать обозначения y(t) [х].

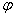Изменение с течением времени состояния системы вызывает движение системы, которое можно задать, если каждому моменту времени t Т по определенному правилу поставить в соответствие состояние z Z, т.е. движение системы будет представлять собой функцию 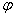: Т ® Z Множество допустимых движений системы определяется на интервале Т: Ф = { 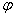: Т® 2}. Множество допустимых начальных движений определяется Ф0 = { 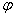о: TxTx 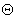® -Z}, где 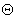= { 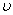} множество возможных величин отрезков 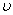. Величина и зависит от памяти системы и может изменяться от t0 до 0 [х].

Множество допустимых входных процессов, определяемых различными функциями на интервале [t0, t], описывается следующим образом:

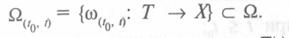
Следовательно, состояние Z(t) системы в момент времени t будет зависеть от начального момента t0 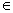Т, текущего времени t 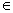Т, начального движения 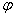0 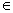Ф0 на отрезке [t — v, t0] и входного процесса 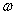(t0, t] 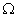(t0,t) на интервале (t0,t)

Таким образом, состояние Z(t) может быть определено с помощью переходной функции состояния:

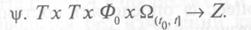
Графически переходная функция представлена на рис. 1.3.

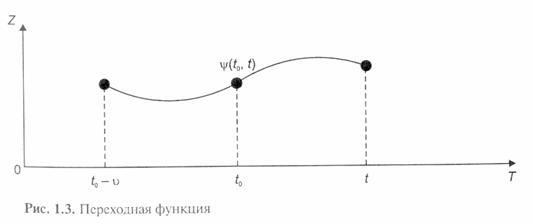
На рис. 1.3 отрезок движения системы 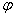на промежутке [t0 — 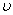, t] будет представлять собой сочленение двух отрезков: 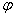0 — начального движения на промежутке [t0 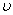, t0] и 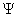(t0,t) — отрезка переходной функции на интервале (t0, t].

Переходная функция состояния должна удовлетворять следующим требованиям.

Во-первых, поскольку знание начального движения системы ф0 на отрезке [t0 - 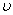,t0] и отрезка входного процесса 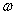(to, t] на интервале (to, t] является необходимым и достаточным условием, позволяющим определить состояние системы Z(t) в момент времени t, то соотношение

Z(t) = 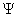(t, t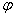0, 0, 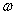(t0,t])

должно быть определено во всех t ³ t0 — .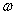

Во-вторых, переходная функция состояния должна быть согласована с начальным движением и начальным состоянием

Z(t) = 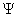(t, t0, 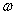(to,t]) = 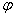0(t, t0, 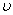) при t £ t0 ;

Z(to) = 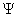(t, t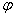0, 0, 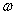(to,t]) = 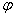0(t, t0, 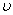) при t £ t0 ;

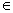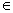для всех t T, z Z, 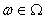,. Эти условия устанавливают также независимость начального движения 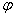0 и начального состояния Z(t0) от значений входного процесса, поскольку 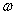(to,t]= 0 при t £ t0.

В-третьих, один и тот же входной процесс со определяет состояние системы на конце интервала времени (t0, t] независимо от того, действовал ли он последовательно, сначала на интервале (t0, t], а затем на интервале (t', t], или на всем интервале (t0, t].

Переходная функция состояния описывает переходный процесс системы.

Переходный процесс системы (процесс системы) — множество преобразований начального состояния и входных воздействий в выходные величины, которые изменяются с течением времени по определенным правилам.

Функцией входа является возбуждение той силы, которая обеспечивает систему энергией, материалом, информацией, поступающей в процесс.

В зависимости от связей входные процессы могут принимать одну (или более) из следующих форм:

1) результат предшествующего процесса, последовательно связанный с данным процессом;

2) результат предшествующего процесса, беспорядочно связанный с данным процессом;

3) результат процесса данной системы, который вновь вводится в нее.

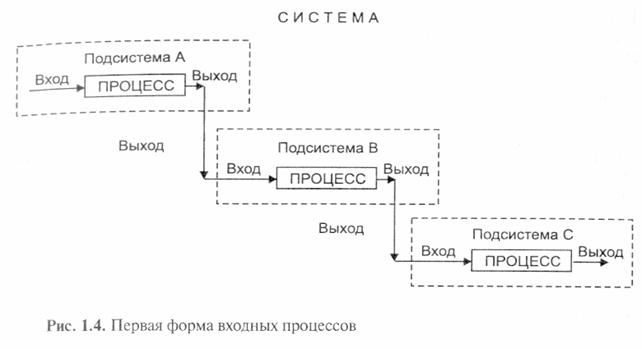
Пример первой формы входных процессов показан на рис. 1.4.

На рис. 1.4 в процессах В и С выходной процесс предыдущей подсистемы вводится без изменений как входной процесс в следующий процесс системы. Процесс А в этом примере является более ранней по времени подсистемой, но не обязательно более простой или более сложной.

Подсистемы А, В и С объединяются в полную систему.

Если несколько подсистем объединены для формирования конечного выхода, частные процессы А, В, С и т.д. связаны так, как показано на рис. 1.5.

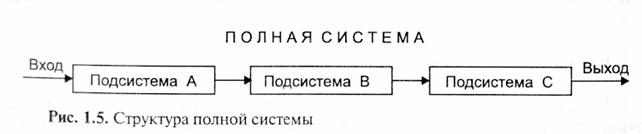
Полная система состоит из всех подсистем, свойств и связей, необходимых для достижения данной цели при данных принуждающих связях. Цель полной системы определяет результат, для достижения которого организуются все ее подсистемы, свойства и связи. Принуждающие связи системы являются ограничениями, накладываемыми на ее действия. Они определяют границу полной системы и дают возможность точно установить условие, при котором она должна действовать.

Вторая форма входных процессов называется беспорядочной (рис. 1.6).

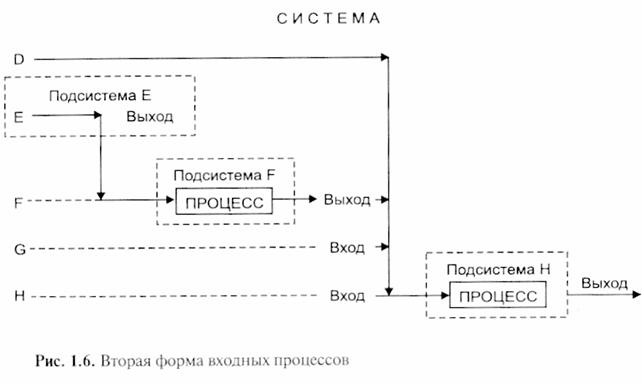
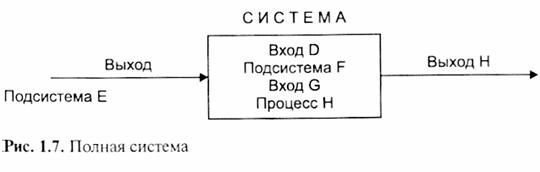
В этом случае входные процессы подсистемы D и G являются входами, вводимыми в случайные моменты времени. Подсистемы D, F, G и Н можно представить как части единого процесса — полную систему (рис. 1.7).

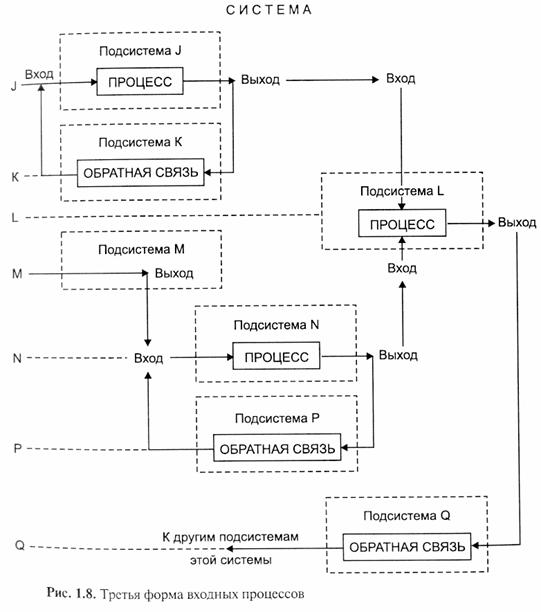
Третья форма входных процессов отличается тем, что в этом случае вход вводится в систему будучи до этого выходом этой же системы. Этот случай иллюстрируется рис. 1.8, где подсистемы К, Р и Q имеют входные процессы связанные с процессом обратной связи.

Рассмотрим процесс "Выход : Вход" между подсистемами более высокого порядка (рис. 1.9).

Чтобы обеспечить подходящий вход в подсистему более высокого порядка, выходы, как это показано на рис. 1.9, могут быть взаимно причинно зависимы. Подсистемы R, S и Т по времени предшествуют подсистемам U, V и X. Они с необходимостью должны предшествовать им, чтобы система могла работать; подсистемы U и V имеют более высокий приоритет по сравнению с R, S, Т и W, но более низкий приоритет, чем подсистема X.

Выход, обозначенный на рис. 1.9 как "Выход : Вход", может автоматически становиться входом, если он вводится в последующую подсистему без изменений, т.е. в этом случае выход и вход идентичны.

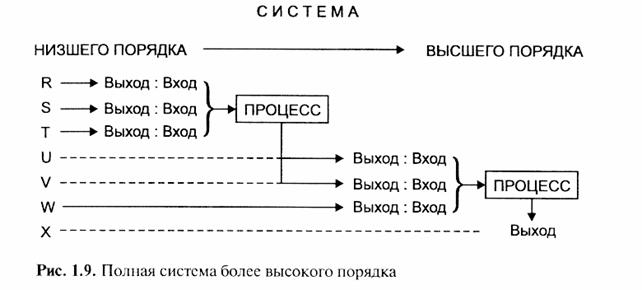
Процессы R, S, Т и U, V, W имеют один выход X. Выход W является выходам от внешней подсистемы, и поэтому он не связан с предыдущей последовательностью системных процессов, имеющих выходы U и V. Никаких ограничений на число выходов во внешнюю среду, кроме возможностей человека и машины воспринимать их, не существует.

Единственное назначение подсистем обратной связи — изменение идущего процесса.

Обратная связь может быть:

1) объектом отдельного процесса подсистемы;

2) объектом интегрированного процесса подсистемы;

3) распределенным по времени объектом, возвращающим выход подсистемы с высшим приоритетом (более поздний по времени) для сравнения с критерием подсистемы низшего приоритета (более раннего по времени).

Схема на рис. 1.10 позволяет пояснить перечисленные виды процессов подсистемы обратной связи.

Интегрированным процессом называется такой, в котором объекты подсистемы теряют свой независимый характер. В интегрированных системах объекты могут быть определены только в контексте подсистемы или системы, к которой они принадлежат.

Подсистема АА на рис. 1.10 предшествует двум подсистемам АВ и АС. Но она играет по отношению к ним разные роли: обратная связь АВ дает вход в подсистему АА (выступает как обратная связь объекта отдельного процесса подсистемы), но, кроме того, выход используется как вход в подсистему АС.

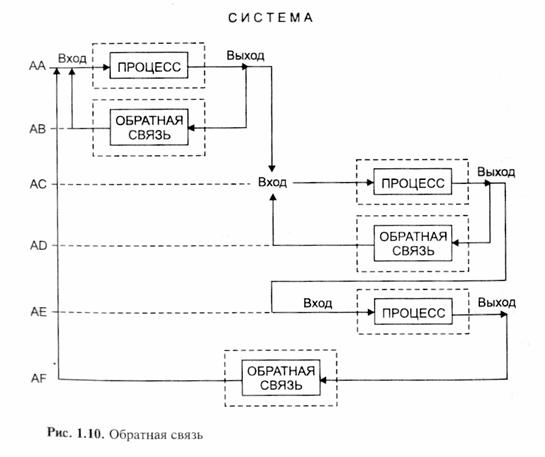
Выход подсистемы АС поступает на входную сторону подсистемы АЕ. Подсистемы АА, АС и АЕ видоизменяются собственными функциями подсистем обратной связи (обратная связь выступает как объект интегрированного процесса подсистем). Кроме того, подсистемы АА, АС, АЕ также изменяются под воздействием результатов последующих действий, например, подсистема АЕ изменяет подсистему АА с помощью обратной связи AF.

Функция ограничения системы складывается из двух частей: цели и принуждающих связей.

Ограничение системы является выходом органа, обозначаемого как потребитель (покупатель) выхода системы.

Системный потребитель (покупатель) воздействует на выход и управление системой, как это показано на рис. 1.11.

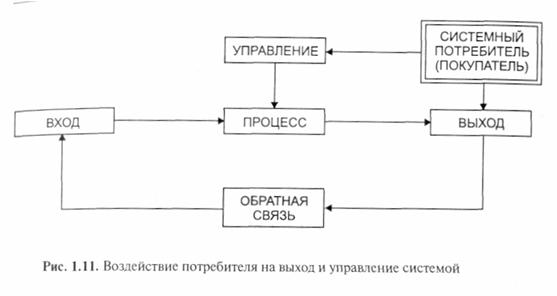. Системные потребители (покупатели) существуют на всех уровнях действия подсистем. Требования к системе диктуются потребителем (покупателем) в форме ограничений.