ОБЩАЯ ХАРАКТЕРИСТИКА ЗЕМЛИ § 1. Форма и размеры Земли

На основании наблюдений за удаляющимся и приближа­ющимся кораблем древние философы пришли к заключению, что Земля — правильный шар. В конце XVII в. французскими уче-

И

ными было замечено, что часы в приэкваториальной части Южной Америки идут медлен­нее, чем в Париже, на 2,5 мин в сутки. Значит, влияние силы тяжести на маятник в Париже и на экваторе различное. И. Ньютон объяснил это явление тем, что Земля сплюснута у полюсов и имеет форму эллип­соида вращения — сфероида. Впервые сжатие Земли (отно­шение разницы между длинами экваториального и полярного

радиусов к длине экваториального радиуса) определил Ф. Бессель в 1841 г. По его расчетам оно равно 1/299,2.

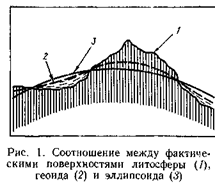
Размеры и форма Земли определены советскими учеными Ф. А. Красовским и др. Согласно их измерениям, форма Земли представляет собой эллипсоид вращения с длиной экваториаль­ного радиуса 6378,245 км и полярного радиуса 6356,863 км. Осью вращения служит малая полярная ось. Сжатие Земли составляет 1/298,3; площадь ее поверхности 510 100 934 км²; объем 1 083 819 780 000 км³. Для геодезических и картографиче­ских работ на территории СССР приняты размеры эллипсоида Красовского. Однако эллипсоид Красовского лишь теоретиче­ски описывает поверхность Земли. Топографическая поверх­ность ее с высочайшими горными вершинами и глубокими океан­скими впадинами имеет значительные отклонения от поверхности эллипсоида вращения. Наиболее близка к топографической поверх­ности Земли поверхность, которая может быть получена, если мысленно продолжить уровень Мирового океана под материками. Тело, описанное такой поверхностью, свойственно только фигуре Земли и называется геоидом. Поверхность геоида во всех точках перпендикулярна к направлению силы тяжести, вследст­вие чего ускорения силы тяжести в этих точках одинаковы. Для получения возможно меньших отклонений поверхности геоида от поверхности сфероида необходимо сфероид правильно ориентиро­вать внутри геоида (рис. 1). Сфероид, ориентированный таким об­разом, называется референц-эллипсоидом.