Задание для самостоятельного выполнения. 1. На плоскости расположена окружность радиуса R с центром в начале координат

1. На плоскости расположена окружность радиуса R с центром в начале координат. Ввести заданные координаты точки и определить, лежит ли она на окружности. Решить задачу при R=2 для точек с координатами (0, 2), (1.5, 0.7), (1, 1), (3, 0).

Указание. Считать, что точка с координатами х, у лежит на окружности радиуса R, если |х²+у² – R²|£10^-3.

2. Определить, лежит ли заданная точка внутри или вне треугольника с вершинами в точках (–1, 0), (1, 0), (0, 1).

Указание. Уравнение прямой, ограничивающей фигуру слева: у = 1+х (х<0), справа: у = 1 – х (х ³ 0). Следовательно, точка принадлежит фигуре, если у ³ 0 и у + |х| £ 1.

3. Для заданных a и b получить С = max(a, b), если а > 0 или С = min(a, b), если а £ 0.

4. Для заданных a, b, c вычислить z=max(min(a, b), c).

5. Заданы площади круга R и квадрата S. Определить, поместится ли квадрат в круге. Задачу решить при: 1).R=70, S=36.74, 2).R=0.86, S=0.74.

6. Для задачи 5 определить, поместится ли круг в квадрате. Задачу решить при:1) R=3.2, S=3.5; 2) R=3.2, S=4; 3) R=6, S=9.

7. Вычислить значение функции y при заданном значении аргумента x по формуле y = 1, если 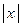>1, или y = 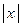, если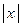 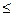1.

8. Вычислить значение функции y при заданном значении аргумента x по формуле у = 0, если ½х½³1, или у = x²–1, если ½х½<1.

9. Вычислить значение функции y при заданном значении аргумента x по формуле у = 0, если х £ –1, или у = 1+х, если ­–1<x£0, или y = 1, если х>0.

10. Вычислить значение функции y при заданном значении аргумента x по формуле y = 1, если х £ –1, или у= –x, если 1<x £1, или y = –1, если х>1.

11. Следующие задачи требует сочетания циклов и разветвлений, а также использования множественного выбора. Предполагается, что количество вводимых исходных данных (n) задано (см. пример 3.2.7).

12. Определить средний рост девочек и мальчиков одного класса. В классе учится n учеников.

13. В компьютер вводятся по очереди координаты n точек. Определить, сколько из них попадет в круг радиусом R с центром в точке (a, b).

14. Ученику 1-го класса назначается дополнительно стакан молока (200 мл), если его вес составляет меньше 30 кг. Определить, сколько литров молока потребуется ежедневно для одного класса, состоящего из n учеников. После взвешивания вес каждого ученика вводится в ЭВМ.

15. В компьютер вводятся по очереди координаты n точек. Определить, сколько из них попадет в кольцо с внутренним радиусом R₁ и внешним R₂.

16. В соревнованиях по бегу принимают участие 30 спортсменов. Вводя по очереди результаты участников, определить, сколько из них выполнили заданный норматив.

17. В компьютер по очереди вводятся координаты n точек. Определить, сколько из них принадлежит фигуре, ограниченной осью абсцисс и аркой синусоиды, построенной для аргумента от 0 до p.

18. В компьютер вводятся координаты n точек, лежащих на плоскости. После ввода координат каждой точки выводить номер квадранта, в котором она находится. Определить количество точек, лежащих по отдельности в 1 и 3 квадрантах.

19. В компьютер вводятся координаты n точек, лежащих на плоскости. Напечатать номер точки, ближайшей к началу координат, и величину расстояния от нее до начала координат.

20. Вводя n значений R, вычислить по выбору площадь квадрата со стороной R, площадь круга радиуса R или площадь равностороннего треугольника со стороной R. Использовать множественный выбор.

21. Для n пар значений А, В вычислить по выбору площадь прямоугольника со сторонами А, В; площадь кольца, заключенного между двумя окружностями с радиусами А и В; площадь равнобедренного треугольника со сторонами А, B, В. Использовать множественный выбор.