Цифровые преобразователи и приборы.
Цифровые измерительные приборы (ЦИП) и системы (ЦИС) имеют следующие достоинства: высокая точность, в том числе и в тяжёлых эксплуатационных условиях; возможность запоминать, передавать на расстояния и вводить в ЭВМ результаты измерений; удобство обслуживания и проведения измерений.
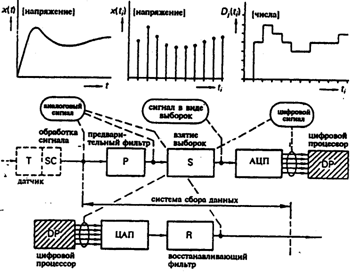
Рисунок 5.1 - Схема сбора данных с одним измерительным каналом ИИС
Измерительные системы с информацией в цифровой форме значительно проще и надёжнее в эксплуатации.
Обычно сигнал, полученный в результате измерения, должен быть подвергнут некоторой обработке, прежде чем он станет удобным для наблюдения, регистрации или управления. Ранее была рассмотрена линейная обработка сигнала, такая как ослабление, усиление и компенсация. Сейчас мы рассмотрим такие преобразования сигналов как аналого-цифровое и цифроаналоговое (см. рисунок 5.1). Это необходимо сделать, чтобы понять работу цифровой измерительной системы (ЦИС) (см. рисунок 5.2).
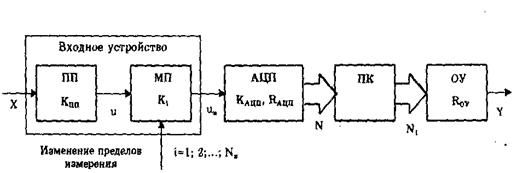
Измеряемая ФВ Х воздействует на первичный измерительный преобразователь (ПП), имеющий коэффициент преобразования КПП. Он преобразует величину Х в электрический сигнал, в качестве которого используется главным образом напряжение, т.е. u = КППХ. Это напряжение, в свою очередь, поступает на масштабный измерительный преобразователь (МП), необходимый для изменения пределов измерения ЦИС.
|
Рисунок 5.2 – Структурная схема ЦИС
Он может иметь разное число диапазонов измерения: от 1 до Nп. Диапазон изменения измеряемой величины Х разбивается на Nп под- диапазонов: X1min,….X1max; X2min,…,X2max; …,XNп min,…,XNп max, где Xi min,…,Xi max –минимальные и максимальные точки i-го диапазона измерений.
Масштабный преобразователь так измеряет (уменьшает или увеличивает) входное напряжение в заданное число К i раз (i = 1;2;…; Nп ), чтобы сигнал uн на его входе был нормирован, т.е. его значение находилось в заданных пределах. Как правило, стараются обеспечить выполнение условий, при которых пределы изменения нормированного напряжения совпадают с большей частью допустимого диапазона изменения входного сигнала аналого-цифрового преобразователя (АЦП) при всех возможных значениях измеряемого сигнала. Нормированное напряжение uн = Ki Kпп X преобразуется АЦП в цифровой код N, имеющий разрядность RАЦП. АЦП выполняется однопредельным, рассчитанным на один фиксированный диапазон изменения входного сигнала uн.
Для преобразования аналогового сигнала в цифровой требуется специальное устройство – аналого-цифровой преобразователь (АЦП), а для обратного преобразования - в цифроаналоговый преобразователь (ЦИП).
|
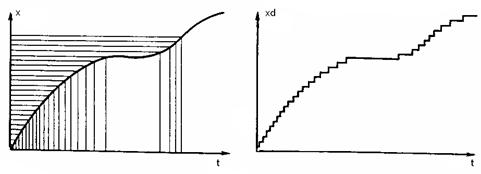
Потребуется ещё средство сглаживания сигнала ступенчатой кривой (см. рисунок 5.3).
а) б)
Рисунок 5.3 – Дискретное представление аналоговой величины (а) и её передача в виде сигнала ступенчатой формы (б)
Подобное свойственно и регистрации результатов – печатание чисел и вычерчивание соответствующей непрерывной кривой на бумажном носителе. Вместо чисел (при цифровой регистрации) может вычерчиваться соответствующая кривая ступенчатой формы, подобно рисунку 5.3. При быстродействии, согласованном со скоростью изменения измеряемой величины x=f(t), аналоговый прибор может непрерывно отслеживать все изменения этой величины. Цифровой прибор фиксирует мгновенные значения измеряемой величины в дискретные моменты времени (определяются моментами отсчётов), а сами эти значения представляются ограниченным числом ступеней квантования по уровню (числом уровней). Так на рисунке 5.3,а вдоль оси ординат х обозначено 23 уровня (не стандартное). Число этих уровней, соответствующее выбранному (отсчитанному) дискретному значению, представляет цифровой эквивалент этого значения. Выбранное число уровней может быть 23 =8, 24 =16, 25 =32, и далее- 64,128,256 и т.д. В нашем примере 1-й уровень имеет цифровой эквивалент в 5-ти разрядном коде -00001, соответственно, 2-ой – 00010, 3-ий – 00011 и т.д. 23-ий уровень будет представлен кодовой комбинацией 23(10) = 1*24+0*23+1*22+1*21+1*20 =10111(2). Как показано на рисунке 5.3,б, измеряемая величина отображается следующей ступенью, если она при своём изменении превзойдёт предыдущий уровень квантования. Точность цифрового представления измеряемой величины определяется шагом временной дискретизации и шагом квантования по уровню.
Принципиальная разница между аналоговыми и цифровыми ИС заключается в том, что в цифровых ИС величины и соответствующие сигналы, квантованные по уровню, могут быть представлены только конечным числом, тогда как аналоговые величины отображаются бесконечно большим числом значений. Так, если индикатор цифровой ИС отображает 3 разряда десятичного числа, то это означает, что количество значений измеряемой величины не превышает 1000 (от 0 до 999), т.е. бесконечно большое число значений измеряемой величины разбит на 1000 равных интервалов с шагом 1/1000 (квантование по уровню), а при измерениях указывается целое число уровней, с округлением относительно истинного значения аналоговой величины.
Анализ свойств и характеристик аналоговых и цифровых методов и СИ не позволяет однозначно утверждать о превосходстве одних перед другими; это зависит от конкретных применений и возможностей конструктивного исполнения. С точки зрения решения измерительных задач можно утверждать, что цифровые ИС позволяют снизить потери информации при отображении результатов, их хранения, передаче и обработке на ЭВМ благодаря соответствующим преимуществам цифровых сигналов перед аналоговыми.
Важной характеристикой ЦИС является метод преобразования аналоговой измеряемой величины в её цифровой эквивалент, реализованный в АЦП.
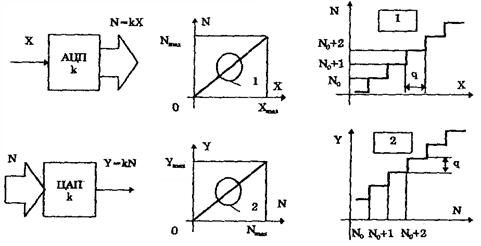
В настоящее время применяются методы поразрядного уравновешивания (метод последовательных приближений), двойного интегрирования и преобразования напряжения в частоту. Обозначения в структурных схемах и передаточные функции АЦП и ЦАП показаны на рисунке 5.4.
а) б) в)
|
Рисунок 5.4 - Обозначения в структурных схемах (а), передаточные функции (б) и части передаточных функций (в) АЦП,ЦАП в увеличенном масштабе
Уравнение преобразования идеального однополярного ЦАП
u = UmN10 / (2R -1) = Um / (2R -1)*(aR-1*2R-1 + aR-2*2R-2 +…+a1*21 +a0*20),
где R- разрядность ЦАП; N10 – значение входного кода в десятичной системе исчисления; ai – коэффициенты, которые могут принимать значения, равные нулю или единице. Из уравнения видно, что квант напряжения на выходе ЦАП, называемый единицей младшего разряда (ЕМР) равен Um / (2R -1).
Уравнение преобразования идеального однополярного АЦП записывается в виде
N10 = int [ u (2R – 1) / Um],
где int[X]- функция, выделяющая целую часть числа Х. Минимальное изменение напряжения на входе АЦП, которое приводит к изменению выходного кода, называемое разрешающей способностью, равно Um / (2R-1).
Метрологические свойства АЦП и ЦИС в целом существенно зависят от номинальной ступени квантования АЦП, равной
q = [uн (Nmax) – uн (Nmin)] / [(Nmax – Nmin) - 1] = [uн (Nmax) – uн (Nmin)]/ M,
где Nmax,Nmin – максимальное и минимальное значения выходного кода АЦП; uн (Nmax), uн (Nmin ) – значения входного напряжения АЦП, соответствующие Nmax и Nmin.
При использовании двоичного цифрового кода максимальное число возможных выходных кодовых комбинаций М = 2RАЦП -1.
большое число значений измеряемой величины разбит на 1000 равных интервалов с шагом 1/1000 (квантование по уровню), а при измерениях указывается целое число уровней, с округлением относительно истинного значения аналоговой величины.
Наиболее простыми являются АЦП косвенного типа, построенные на основе преобразователя напряжение – время (ПНВ) и напряжение – частота (ПНЧ).
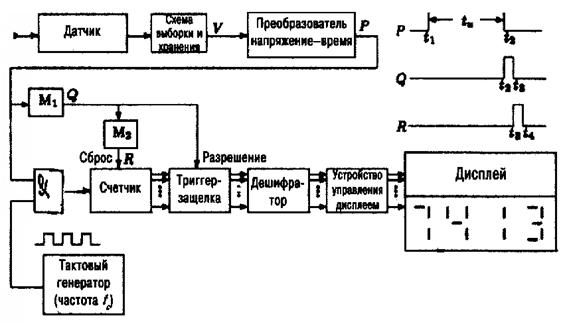
Измерение физической величины (ФВ) (см. рисунок.5.5) производится в несколько этапов:
- ФВх (генераторная или параметрическая) при помощи соответству-ющего датчика преобразуется в электрический сигнал – напряжение v;
- значение напряжения v запоминается в устройстве выборки и хранения в виде величины V на время проведения цикла измерения;
- величина V преобразуется в одиночный импульс (серию импульсов), длительность tx которого пропорциональна значению напряжения V.
Устройство, осуществляющее данное преобразование и есть ПНВ:
- интервал времени tx измеряется путём заполнения его импульсами стандартной длительности Тх от тактового (счётного) генератора образцовой частоты fc. Эти импульсы подсчитываются счётчиком и в дальнейшем преобразуются в двоичное число. Преобразование ФВ в интервал времени и последующее измерение его длительности - основа АЦП;
- информация в виде двоичного кода преобразуется в десятичный код и отображается на экране алфавитно – цифрового дисплея.
|
Рисунок 5.5 – Цифровое измерение физической величины
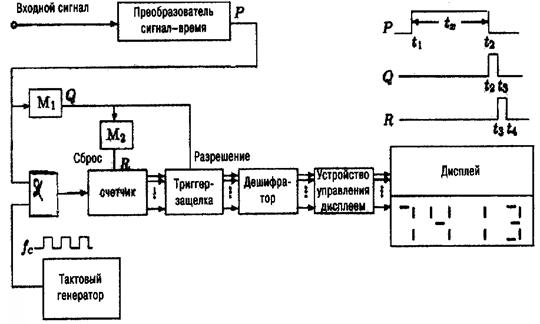
Рассмотрим принцип построения и работы АЦП с ПНВ, известный как АЦП с время импульсным преобразованием ВИП (см. рисунок 5.6).
Счётчик подсчитывает импульсы, поступающие с тактового генератора, в течение времени tx. По окончании этого измерительного интервала в момент времени t2 одновибратор (мультивибратор) M1 вырабатывает короткий импульс, по которому триггер – защёлка запоминает содержимое счётчика на этот момент.
|
В момент времени t3 на счётчик поступает импульс от одновибратора M2 и его показания сбрасываются. Таким образом, электронный вентиль, пропускающий на счётчик импульсы с частотой fc, открыт только в течение интервала tx , а в остальное время закрыт.
Рисунок 5.6 - АЦП на основе преобразователя сигнал – время
Если N есть число импульсов за время tx, то N = f с tx, или N º tx.
|
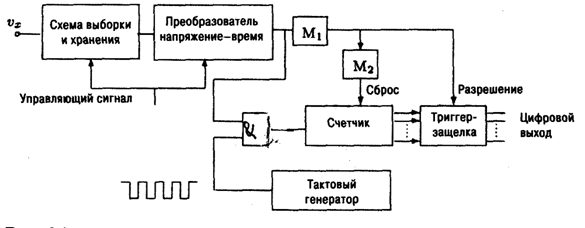
Рисунок 5.7 – АЦП, на основе преобразователя напряжение –время
Если использовать конкретный преобразователь напряжение –время, то схема АЦП выглядит несколько иначе (см. рисунок 5.7).
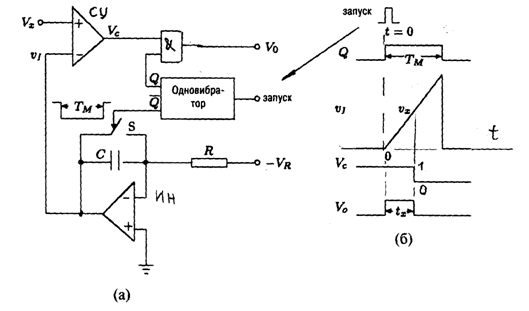
В качестве ПНВ рассмотрим преобразователь напряжение – время на основе однократного интегрирования (на основе компаратора и одновибратора) (см. рисунок 5.8).
|
Рисунок 5.8 – Преобразователь напряжение – время на основе компаратора и одновибратора (а) и временные диаграммы сигналов (б)
Управление ПНВ осуществляется подачей импульса запуска на одно-вибратор. Одновибратор (ОВ) – электронное устройство, предназначенное для формирования прямоугольного импульса напряжения требуемой длительности ТМ. В начальный момент времени t = 0¯ выходной сигнал ОВ на прямом выходе нулевой Q = 0, а на инверсном выходе (обратный сигнал) - Q = 1.Так как интегратор Ин закорочен ключём S, то компенсационное напряжение vI = 0.
На прямой вход устройства сравнения (компаратор) СУ подаётся измеряемое напряжение Vx > 0, поэтому на его выходе имеем напряжение Vc = 1. На выходе электронного вентиля Vo = 0. В момент времени t =0 запускается ОВ: Q = 1 и уровень сигнала Vo становится высоким, т.е.равным 1. Ключ S открывается и интегратор начинает интегрировать постоянное напряжение - VR.
Выходное напряжение Ин vI возрастает линейно во времени и при t = tx vI = Vx. В этот момент срабатывает компаратор и уровень сигналов Vc и Vo
становится низким – нулевым. Из схемы и временных диаграмм сигналов видно, что tx = RC Vx / VR.
Очевидно, что ширина импульса одновибратора TM > t xmax, соответствующего максимальному напряжению Vx, т.е. следующее преобразование возможно через интервал TM.
АЦП, показанный на рисунке 5.7, относится к АЦП косвенного типа, поскольку для преобразования сигналов он использует ПНВ.
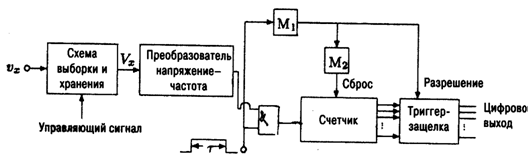
Другой АЦП косвенного типа использует преобразователь напряжение – частота ПНЧ (см. рисунок 5 .9).
|
Рисунок 5.9 – АЦП, на основе преобразователя напряжение – частота
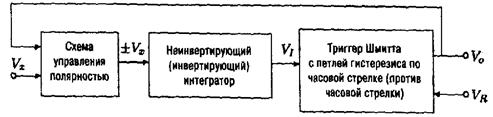
На рисунке 5.10 а представлена структурная схема одного ПНЧ, известного как преобразователь напряжение – частота двойного интегрирования.
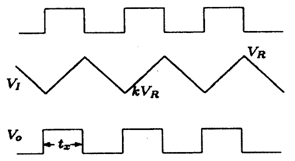
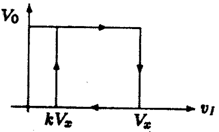
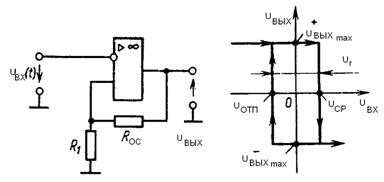
В зависимости от уровня выходного сигнала Vo схема управляет полярностью и подаёт на интегратор напряжение Vx разной полярности. Когда уровень Vo высокий, Vx будет иметь положительную полярность и наоборот (см. рисунок 5.10,б). Напряжение прямоугольной формы Vx поступает на вход интегратора. В процессе преобразования участвуют обе части выходного сигнала интегратора VI. Сигнал VI управляет триггером Шмитта. Триггер Шмитта – это компаратор с положительной обратной связью (см. рисунок 5.11) с характеристикой переключения, представленной на рисунке 5.10,в.
Наибольшее распространение получили АЦП напряжение – время двойного (двухтактного интегрирования) (см. рисунок 5.12).
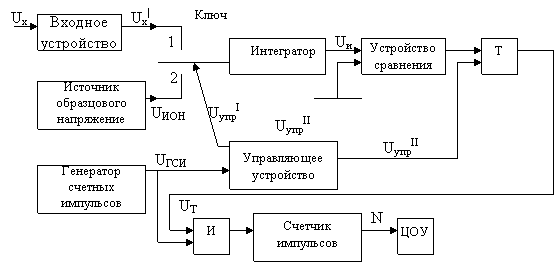
Схема содержит входное устройство, трёхпозиционный ключ, интегратор Ин, источник образцового напряжения ИОН, устройство сравнения СУ, триггер Тг, генератор счётных (образцовых импульсов) ГСИ, управляющее устройство УУ, логическую схему И (схему совпадения, электронный ключ, временной селектор), счётчик импульсов Си и цифровое отсчётное устройство ЦОУ.
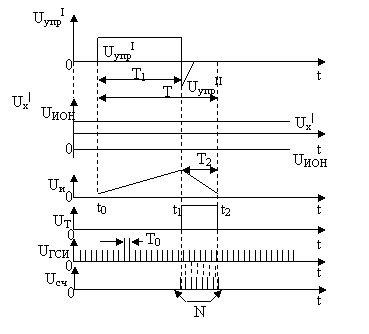
Вначале цикла измерения при t=to УУ вырабатывает калиброванный импульс U´упр с длительностью T1=ToK, где To - период следования счётных импульсов; K - ёмкость счётчика.
В момент появления фронта импульса U´упр ключ переводится в положение 1, и с входного устройства на интегратор поступит напряжение U´x, пропорциональное измеряемому напряжению Ux.
|
а)
б) в)
Рисунок 5.10 – Структурная схема ПНЧ двойного интегрирования (а),
временные диаграммы сигналов (б), передаточная характеристика по напряжению триггера Шмитта (в)
а) б)
Рисунок 5.11 – Схема (а) и амплитудная характеристика
(б) триггера Шмита
Затем на интервале времени T1 = t1 – to происходит интегрирование напряжения U´x (пропорциональное измеряемому Ux), в результате чего нарастающее напряжение на выходе интегратора будет определяться формулой
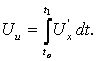
В момент времени t=t1 управляющий сигнал U“упр, поступающий с УУ, переводит ключ в положение 2 и на Ин с ИОН поступает образцовое отрицательное напряжение Uион. Одновременно с этим другой управляющий сигнал U“упр опрокидывает триггер.
Интегрирование напряжения –Uион происходит быстрее, так как в схеме установлено | Uион | ³ U´x . Интегрирование образцового напряжения продолжается до тех пор, пока выходное напряжение Ин снова не станет равным нулю ( при этом T2 = t2 – t1). Поэтому в течение времени второго интервала на выходе Ин формируется спадающее напряжение
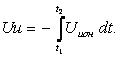
При этом длительность интервала интегрирования T2 не больше, чем выше амплитуда измеряемого напряжения U´x .
|
а)
б)
Рисунок 5.12 - Структурная схема преобразователя с двойным
интегрированием
В момент времени t= t2 напряжение Uи на выходе Ин становится равным нулю и устройство сравнения (второй вход которого соединён с корпусом) выдаёт сигнал на Тг, возвращая его в исходное состояние. На его выходе формируется импульс Uт длительностью T2, поступающий на вход схемы И. На другой её вход подается сигнал UГСИ с ГСИ. По окончании импульса Uт, поступающего с Тг, процесс измерения прекращается.
Преобразование измеряемого временного интервала T2 в эквивалентное число импульсов N осуществляется по электронному методу счётных импульсов – заполнением указанного интервала периодическими импульсами ГСИ и подсчётом их числа Си. На Си, а значит, и на ЦОУ записывают число импульсов NUсч, пропорциональное измеряемому напряжению  Ux:
Ux:
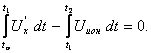
Из этого выражения можно получить следующие формулы:
T1=ToK; T2 » ToN ; U´x Т1= UИОНT2,
откуда поучаем U´x = UИОН N / K.
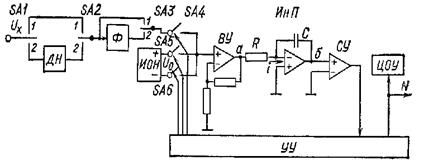
Структурная схема цифрового устройства по методу двойного интегрирования несколько иного плана показана на рисунке 5.13.
|
Рисунок 5.13 – Структурная схема цифрового прибора по методу двойного интегрирования
Измеряемое напряжение Ux непосредственно (переключатели SA1, SA2 в позиции 1) или через делитель напряжения ДН (SA1, SA2 в позиции 2), с помощью которого выбирается нужный поддиапазон измерения, затем через фильтр Ф (SA3 в позиции 2), или непосредственно (SA3 в позиции1) подаётся на ключ SA4. Система ключей SA4, SA5, SA6 предназначена для подачи на входной усилитель ВУ измеряемого или одного из опорных напряжений положительной или отрицательной полярности, последние вырабатываются источником опорных напряжений ИОН в виде высокостабильных одинаковых по абсолютной величине, но разных по знаку напряжений постоянного тока.
ВУ представляет собой усилитель постоянного тока с большим входным сопротивлением (более 1000 МОм) и регулируемым посредством отрицательной обратной связи ООС коэффициентом усиления. Если Ux < 10 В, то оно подаётся на входное устройство ВУ непосредственно (SA1, SA2 в позиции1); при этом входное сопротивление ВУ более 1000 МОм. Если же Ux >10 В, то оно подаётся на ДН (SA1, SA2 в позиции 2) и входное сопротивление определяется сопротивлением ДН, которое обычно 10 МОм. При измерении напряжений менее одного вольта, например, на поддиапазонах 0,1 и 0,01В, коэффициент усиления ВУ выбирают соответственно равным 10 или 100 с тем, чтобы напряжение на выходе ВУ изменялось в одних пределах независимо от выбранного поддиапазона измерения.
К выходу ВУ подключён интегрирующий преобразователь ИнП на основе операционного усилителя с конденсатором в цепи ООС. Резистор R преобразует входное напряжение ИнП в пропорциональное значение тока ix = UxKд Kу / R, где Kд и Kу – коэффициенты передачи ДН и ВУ; для выключенного ДН ( SA1, SA2 в позиции 1) Kд = 1. Этот ток, если пренебречь входным током усилителя ИнП, протекает через конденсатор С и заряжает его, при этом входное напряжение ИнП возрастает.
Обозначим U1 напряжение на выходе ИнП (в точке б рисунка 5.13) в момент t1 окончания заряда конденсатора
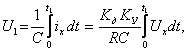
Обозначим далее Uxср среднее значение измеряемого напряжения на интервале от 0 до t1, тогда
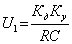 Uxср t1 .
Uxср t1 .
В момент времени t = t1 ключ SA4 размыкается и замыкается SA5 или SA6. Теперь на вход ВУ подаётся опорное напряжение, полярность которого выбирается так, чтобы оно было противоположным полярности Ux и снимало заряд с конденсатора С, накопленный за время замкнутого состояния SA4. На рисунке 5.14,а показана временная диаграмма напряжения в точках а и б схемы.
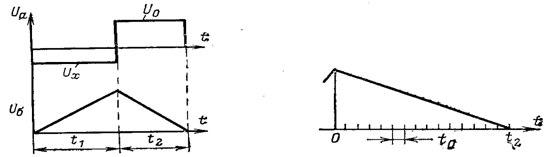
а) б)
Рисунок 5.14 – Временные диаграммы АЦП двойного интегрирования
На диаграмме видно два такта в цикле работы преобразователя: первый такт длительностью t1 соответствует заряду конденсатора С, второй такт длительностью t2 – его разряду.
Это и послужило основой для названия метода преобразования – двухтактное интегрирование.
Момент окончания интервала t2 соответствует моменту прохождения выходным напряжением ИнП через нулевой уровень, что фиксируется сравнивающим устройством СУ. Напряжение U2, до которого разрядится конденсатор за время t2, равно
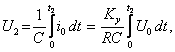
где io = Uo / R – входной ток интегрирующего преобразователя, вызываемый напряжением Uo.
Значение Uo постоянно и во времени не меняется, поэтому
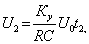 .
.
Так как напряжение на выходе ИнП в начале и в конце цикла измерения равно нулю, то справедливо равенство U1 = U2. Поставим, полученные выше выражения, получим KдUxсрt1=Uot2, откуда  t2 = (Kд t1)/ Uo × Uxср.
t2 = (Kд t1)/ Uo × Uxср.
Величины Kд, t1 и Uo выбираются постоянными, что обеспечивает зависимость между Uxср и t2 вида прямой пропорциональности.
Интервал t2 измеряется путём заполнения импульсами напряжения высокой частоты генератора импульсов со стабильным периодом to (см. рисунок 5.14.б) и последующим их подсчётом. Обозначим N число импульсов, которое укладывается на интервале t2, тогда
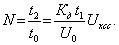
Интервал времени t1 обычно задаётся тем же генератором высокой частоты путём подсчёта счётчиком импульсов определённого числа No периодов колебаний этого генератора t1 = Noto. Подставив значение t1 в уравнение для N, получим окончательно
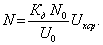
Величины Кд и Uo стабильны, а No – число, поэтому связь между N и Uxср отличается высокой стабильностью.
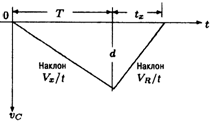
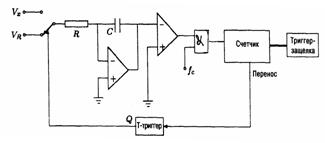
Преобразователь по методу двойного интегрирования можно представить в виде (см. рисунок 5.15).
| 
| ||
а) б)
Рисунок 5.15 –Временная диаграмма (а); упрощённая схема (б) преобразователя двойного интегрирования
Интегрирующий конденсатор сначала заряжают при помощи входного напряжения Vx в течение известного времениT1, а потом разряжают за время tx , подключив его к источнику опорного напряжения -VR, как показано на рисунке 5.15,а.
Из рисунка видно, что
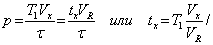 .
.
Значит tx пропорционально Vx. Схема такого преобразователя называется преобразователем двухтактного интегрирования.
Точное значение интервала времени T1 можно определить при помощи счётчика импульсов. И для преобразования информации в двоичный код, и для установки интервала T1 используется один и тот же счётчик. При этом значение T1 задаётся 2NТс . Значение tx будет максимальным, когда напряжение Vx максимально и равно Vm. Поэтому максимальное время преобразования определяется выражением
Тc = Т1 + max tx = 2 T1 = 2 N+1 Тc .
Отсюда видно, что на одно преобразование напряжения в цифровой код требуется 2 N+1 периодов тактового генератора. Несмотря на то, что преобразователи данного типа не обладают высоким быстродействием, они широко применяются в ИИС. Число импульсов, подсчитанных в течение интервала времени tx, равно
fctx = fcT1 Vx / VR = 2N Vx/ VR .
Отсюда
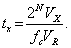
Дата добавления: 2015-02-05; просмотров: 3178;
