ЭЛЕКТРОМАГНЕТИЗМ. Связь магнитной индукции с напряженностью магнитного поля

Связь магнитной индукции 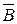с напряженностью 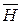магнитного поля

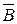=μ μ ,

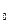
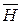где μ — магнитная проницаемость изотропной среды; μ 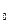— магнитная постоянная. В вакууме μ =1, и тогда магнитная индукция в вакууме

.

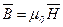Закон Био-Савара-Лапласа

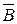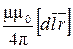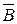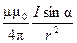d = или d= d,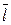

где 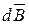— магнитная индукция поля, создаваемого эле­ментом про­вода длиной dl с током 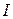; 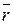- радиус-вектор, направленный от эле­мента проводника к точке, в которой определяется магнитная индук­ция; α — угол между ра­диусом-вектором и направлением тока в эле­менте про­вода.

Магнитная индукция в центре кругового тока

,

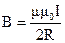где R — радиус кругового витка.

Магнитная индукция на оси кругового тока

,

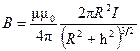где h — расстояние от центра витка до точки, в которой определяется магнитная индукция.

Магнитная индукция поля прямого тока

, ,

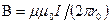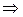
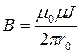где 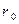— расстояние от оси провода до точки, в которой определяется магнитная индукция.

Магнитная индукция поля, создаваемого отрезком провода с током (см. рис.1, а и пример 1),

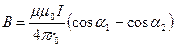
Обозначения ясны из рисунка.

Направление вектора магнитной индукции 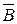обозначено точкой —это значит, что 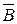направлен перпендикулярно плоскости чертежа к нам.

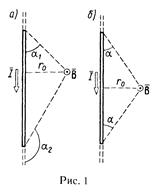При симметричном располо­жении концов провода относи­тельно точки, в которой опреде­ляется магнитная индукция (рис.1,б), 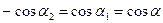, тогда

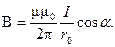
Магнитная индукция поля соле­ноида ,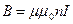

где n — отношение числа витков соле­ноида к его длине.

Сила, действующая на провод с током в магнитном поле (закон Ампера),

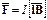, или ,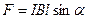

где l — длина провода; 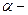гол между направлением тока в проводе и вектором магнитной индукции 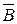. Это выражение справедливо для однородного магнитного поля и прямого отрезка провода. Если поле неоднородно и провод не является прямым, то закон Ампера можно применять к каждому элементу провода в от­дельности:

.

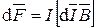Магнитный момент плоского контура с током

,

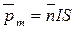где 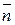— единичный вектор нормали (положительной) к плоскости контура; I — сила тока, протекающего по кон­туру; S — площадь кон­тура.

Механический (вращательный) момент, действующий на контур с то­ком, помещенный в однородное магнитное поле,

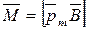, или ,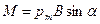

где α - угол между векторам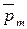и и .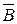

Потенциальная энергия (механическая)* контура с током в магнитном поле

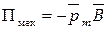, или .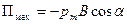

Отношение магнитного момента 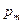к механическому L (мо­менту импульса) заряженной частицы, движущейся по крутой орбите,

,

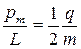где q - заряд частицы; m — масса частицы.

Сила Лоренца

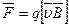, или ,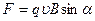

где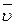— скорость заряженной частицы; 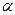— угол между векторам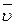и и .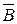

Магнитный поток:

а) в случае однородного магнитного поля и плоской поверхно­сти

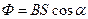, или Φ = B 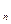S,

где S — площадь контура; α — угол между нормалью к плоскости контура и вектором магнитной индукции;

б) в случае неоднородного поля и произвольной поверхности

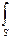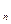Ф = B dS

(интегрирование ведется по всей поверхности).

Потокосцепление (полный поток)

Ψ = ΝΦ.

Эта формула верна для соленоида и тороида с равномер­ной намоткой плотно прилегающих друг к другу N вит­ков.

Работа по перемещению замкнутого контура в магнитном поле

А = .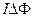

ЭДС индукции

.

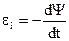Разность потенциалов на концах провода, движущегося со скоростью 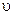в магнитном поле,

,

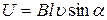где 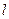— длина провода; α — угол между векторам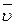и и 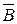. Заряд, протекающий по замкнутому контуру при из­менении магнитного по­тока, пронизывающего этот контур,

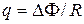, или ,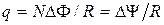

где R — сопротивление контура.

Индуктивность контура

.

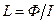ЭДС самоиндукции

.

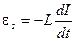Индуктивность соленоида

,

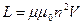где n — отношение числа витков соленоида к его длине; V — объем соленоида.

Мгновенное значение силы тока в цепи, обладающей сопро­тивлением R и индуктивностью L:

а) 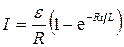(при замыкании цепи), где 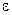— ЭДС источника тока; t — время, прошедшее после замыкания цепи;

б) 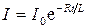(при размыкании цепи), где 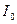- сила тока в цепи при t =0; t — время, прошедшее с момента размыкания цепи.

Энергия магнитного поля

.

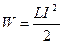Объемная плотность энергии магнитного поля (отно­шение энергии магнитного поля соленоида к его объему)

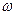=ВH/2, или 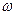= 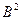/(2 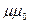), или = ,

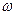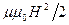где В — магнитная индукция; H — напряженность маг­нитного поля.