Последовательность расчета
Передаточное отношение u = n1/ n2 = 960/350 = 2,74
Угловая скорость ведущего шкива ω1 = π n1/30= 3,14*960/30 = 100,5 рад/с.
Крутящий момент Т1 = N/ ω1 = 7,5*103/100,5 = 74,6 Н*м.
По таблице 5.4 выбираем ремень сечения Б.Для обеспечения большей долговечности ремня выбираем D1 = 140 мм. С учетом относительного скольжения (ε= 0,01) диаметр ведомого шкива D2 = u* D1*(1 – ε)= 2,74*140*(1- 0,01) = 345 мм.
Определяем межосевое расстояние в интервале
аmin = 0,55(D1 + D2) + h =0,55*(140 + 345) + 10,5 = 277 мм;
аmах = 2*(D1 + D2) = 2*(140 + 345) = 970 мм. Принимаем а =500 мм.
Длины клиновых ремней
по ГОСТ 1284-68, мм:
400; (425); 450; (475); 500; (530) – 0. 560; (600); 630; (670); 710; (750) – 0; А
800; (850); 900; (950); 1000; (1060);1120; (1180); 1250; (1320); 1400;(1500); 1600; (1700) - 0; А; Б. 1800; (1900); 2000; (2120); 2240;(2360); 2500 - 0; А; Б; В. (2650); 2800; (3000) - А; Б; В. 3150; (3350); 3550; (3750); 4000
- А; Б; В; Г
Таблица 6.4
| Сечение ремня | D 1, мм | Скорость ремня, м/с | |||||
| О (1320) | ≥ 90 | 0,15 0,17 0,20 0,21 | 0,36 0,39 0,45 0,49 | 0,69 0,78 0,85 0,93 | 1,03 1,15 1,21 1,33 | 1,26 1,38 1,51 1,67 | 1,18 1,26 1,47 1,62 |
| А (1700) | ≥ 125 | 0,37 0,37 0,37 0,44 | 0,74 0,81 0,81 0,96 | 1,33 1,40 1,47 1,69 | 1,69 1,87 2,63 2,29 | 1,84 1,99 2,41 2,65 | 1,69 1,91 2,29 2,65 |
| Б (2240) | ≥ 180 | 0,59 0,66 0,74 0,81 | 1,10 1,25 1,40 1,55 | 2,06 2,23 2,50 2,72 | 2,88 3,16 3,60 3,82 | 2,94 3,60 4,35 4,71 | 2,50 3,24 4,35 4,94 |
| В (3750) | ≥ 280 | 1,03 1,10 1,25 1,33 | 2,14 2,42 2,65 2,88 | 3,68 4,27 4,64 5,00 | 5,28 5,97 6,34 7,07 | 6,25 7,15 7,50 7,80 | 5,90 6,70 7,73 8,10 |
| Г (6000) | ≥ 450 | - - - - | 4,71 5,15 5,59 6,10 | 8,45 9,20 10,1 11,0 | 11,0 12,1 13,5 14,6 | 11,9 13,7 15,7 17,0 | 10,1 13,3 15,8 17,3 |
(4250) - Б; В; Г
4500; (4750); 5000; (5300); 5600; (6000);
- Б; В; Г; Д
6300- Б; В; Г; Д; Е
(6700); 7100;
(7500);8000;(8500);
9000; (9500); 10000
- В; Г; Д; Е
Размеры в скобках – это 2-й ряд, то есть таких ремней выпускается меньше, чем ремней 1-го ряда.
Определяем расчетную длину ремня по формуле (4.37)
L = 2а + π*( D1 + D2)/2 + (D2 - D1)2/4а =
= 2*500 + 3,14*(140 + 345)/2 + (345 -140)2 / (4*500)= 1782 мм.
Ближайшая длина по ГОСТ 1284-68 – 1800 мм.
Вычисляем
Dср = 0,5*(D1 + D2) =0,5*(140 + 345) = = 242,5 мм.
Уточняем межосевое расстояние по формуле
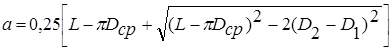 (4.38)
(4.38)
а= 0,25*[1800 – 3,14*242,5 +√(1800 – 3,14*242,5)2 – 2*(345 – 140)2] = 509 мм.
Определяем угол обхвата меньшего шкива ремнем по формуле (4.35)
α10 = 1800 - 60*( D2 - D1)/ а = 180 – 60*(345 – 140)/509 = 1560.
Определяем скорость ремня
v = 0,5 ω1* D1 = 0,5*100,5*140*10-3 = 7 м/с.
По таблице 6 (интерполируя) находим мощность N0, передаваемую одним ремнем
N0 = 1,25 + (2,23 – 1,25)*2/5 = 2,64 кВт.
Ориентировочное число ремней z = N/ N0 = 7,5/2,64 = 2,8 = 3 ремня.
Определяем мощность N1, передаваемую одним ремнем с учетом условий работы передачи по формуле
N1 = N0* CzCαCLCp (4.39)
Cz – учитывает неравномерность распределения нагрузки между ремнями
z …… 2…3 4…6 6
Cz ……0,95 0,9 0,85
Cα = 1 – 0,003*(180 - α10) = 1 – 0,003*(180 – 156) = 0,928
CL – учитывает влияние длины ремня
CL = 0,3* L/ L0 + 0,7 = 0,3*1800/2240 + 0,7 = 0,94
Cp = 0,9 – 0,1 = 0,8 (умеренные колебания нагрузки; двухсменная работа)
N1 = N0* CzCαCLCp = 2,64*0,95*0,928*0,94*0,8 = 1,75 кВт.
Необходимое число ремней z = N/ N1 = 7,5/1,75 = 4,3. С учетом того, что Cz будет 0,9, z = 4,54. Необходимо установить 5 ремней сечением Б и длиной L = 1800 мм.
Определяем усилия в клиноременной передаче, приняв напряжение от предварительного натяжения σ0 = 1,6 МПа.
Окружное усилие Р = N/ v = 7,5*103/7 = 1071 Н.
Предварительное натяжение каждой ветви ремня
S0 = σ0*А = 1,6*138 = 221 Н.
Рабочее натяжение ведущей ветви
S1 = S0 + Р/(2 z) = 221 + 1071/10 = 328 Н
Рабочее натяжение ведомой ветви S2 = S0 - Р/(2 z) = 221 - 1071/10 = 114 Н
Усилие на валы Q = 2 S0* z* sin(α1/2) = 2*221*5* sin 780 = 2162 Н.
Шкивы клиноременных передач
Канавки шкивов для клиновых ремней показаны на рис. 4.19.
 В таблице 7.4 приведены размеры канавок, а так же угла φ при различных диаметрах шкивов.
В таблице 7.4 приведены размеры канавок, а так же угла φ при различных диаметрах шкивов.
| Сече ние ремня | c | e | t | s | Расчетные диаметры при угле φ | |||
| О А Б В Г | 2,5 3,3 4,2 5,7 8,1 | 7,5 14,5 | 22,5 | 12,5 | ≥ 63 ≥ 90 ≥ 125 - - | ≥ 80 ≥ 125 ≥ 180 ≥ 200 ≥ 315 | ≥ 112 ≥ 180 ≥ 250 ≥ 355 ≥ 500 | ≥ 180 ≥ 450 ≥ 560 ≥ 710 ≥ 1000 |
Таблица 7.4
Рис.4.19
Шероховатость рабочих поверхностей
Ra ≤ 2,5 мкм.
4.6 Цепные передачи
Достоинства цепных передач по сравнению с ременными – отсутствие проскальзывания, компактность (они занимают меньше места по ширине), меньше нагрузки на валы и подшипники, больший КПД (до 98%). Недостатки цепных передач: удлинение цепи при эксплуатации; повышенные динамические нагрузки; шум при работе; необходимость внимательного ухода при эксплуатации.
Приводные цепи по конструкции бывают: втулочные; роликовые; зубчатые; фасоннозвенные. В приводах общего назначения применяют в основном приводные роликовые цепи. Они выпускаются следующих модификаций: ПРЛ – приводные роликовые легкой серии; ПР – нормальной серии; ПРУ – усиленные; ПРД – длиннозвенные; ПРИ – с изогнутыми пластинами. Наиболее распространены цепи нормальной серии: однорядные – ПР; двухрядные – 2ПР.
 Схема цепной передачи показана на рис. 4.20.
Схема цепной передачи показана на рис. 4.20.
Для уменьшения динамических нагрузок на цепь и звездочки в открытых передачах ограничивают v ≤ 7м/с. Допускаемые значения частот вращения меньшей звездочки n1 приведены в таблице 8.4.
Таблица 8.4
| Шаг t, мм | n1, об/мин | Шаг t, мм | n1, об/мин | |
| 12,7 15,875 19,05 25,4 | 31,75 38,1 44,45 50,8 |
Рис. 4.20
Число зубьев z1 ведущей звездочки выбирают в зависимости от передаточного отношения u. Рекомендуется
z1 = 31 -2 u. z2 = z1* u.
Методику расчета цепной передачи рассмотрим на примере.
Дано: передаваемая мощность N = 5 кВт; n1 = 500 об/мин;
n2 = 200 об/мин; расположение передачи вертикальное; работа в 3 смены; смазка периодическая; нагрузка спокойная.
Решение:
Вычисляем угловую скорость ведущей звездочки
ω1 = πn1/30 = 3,14*500/30 = 52,3 рад/с.
Крутящий момент Т1 = N/ ω1 = 5000/52,3 = 95,6 Н*м = 95,6*103 Н*мм.
Передаточное отношение u = n1/ n2 = 500/200 = 2,5
Число зубьев ведущей звездочки z1 = 31 -2 u = 31 – 5 = 26
Шаг цепи t определяется по формуле
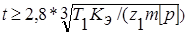 (4.40)
(4.40)
Здесь Кэ = kД*kа*kН*kр*kсм*kп; kД – учитывает характер нагрузки,
kД = 1 при спокойной нагрузке, kД = 1,25…2,5 при ударной нагрузке;
kа – учитывает влияние межосевого расстояния, рекомендуется а = (30…50)t, при этом kа = 1, при а ≤ 25t - kа = 1,25; kН – учитывает влияние наклона цепи; при наклоне до 600 kН = 1, при наклоне свыше 600 kН = 1,25; kр – учитывает способ натяжения цепи, kр = 1 при автоматическом натяжении, kр = 1,25 при периодическом натяжении цепи; kсм – учитывает способ смазки,
kсм = 0,8 при постоянной (картерной) смазке, kсм = 1 при капельной смазке, kсм = 1,3…1,5 при периодической смазке; kп – учитывает периодичность работы, kп = 1 при односменной работе, kп = 1,25 при двухсменной работе,
kп = 1,5 при трехсменной работе. m – число рядов цепи.
[p] – допускаемое давление в шарнирах, МПа (таблица 9.4).
В нашем случае
Кэ = kД*kа*kН*kр*kсм*kп = 1*1*1,25*1,25*1,4*1,5 = 3,28.
Приняли а = 40 t; m = 1; [p] = 20 МПа (ориентировочно).

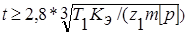 = 2,8*3√95,6*103*3,38/(26*1*20)= 23,9 мм.
= 2,8*3√95,6*103*3,38/(26*1*20)= 23,9 мм.
Таблица 9.4. Допускаемое давление [p], МПа
| n1, об/мин | Шаг цепи t, мм | |||||||
| 12,7 | 15,875 | 19,05 | 25,4 | 31,75 | 38,1 | 44,45 | 50,8 | |
| - | - - | - - - | - - - | |||||
| Разрушающая нагрузка Q, кгс (m = 1) | ||||||||
| Примечания: 1 – если z1 ≠ 17, то [p] умножить на kz = 1 + 0,01(z1 – 17); 2 - для двухрядных цепей [p] уменьшить на 15 %; 3 - Q∑ ≈ Q* m |
Принимаем t = 25,4 мм . Определяем скорость цепи
v = z1* t* n1/(60*103) = 26*25,4* 500/60000 = 5,5 м/с.
Окружное усилие Р = N/ v = 5000/5,5 = 909 Н.
Нагрузка на валы Qв ≈ 1,15*Р = 1,15*909 = 1045 Н. Коэффициент 1,15 учитывает центробежную силу и собственный вес цепи.
Коэффициент запаса прочности n = 9,81* Q/ Qв = 9,81*5670/1045 = 53,2 , что значительно больше нормативного. Нормативный коэффициент запаса прочности берется в пределах 7…15. При этом меньшие значения принимаются при минимальной частоте вращения ведущей звездочки, а большие – при максимальной частоте вращения.
По всем параметрам проходит Цепь ПР-25,4-5670 ГОСТ 13568-75.
Геометрический расчет передачи
z2 = z1* u = 26*2,5 = 65. Межосевое расстояние а = 40 t = 40*25,4 = 1016 мм.
Число звеньев цепи определяется по формуле
Lt =2аt + 0,5z∑ + ∆2/ аt , (4.41)
где аt = а/ t = 1016/25,4 = 40; z∑ = z1 + z2 = 26 + 65 = 91;
∆ = (z2 – z1)/2π = 39/6,28 = 6,2.
Lt =2аt + 0,5z∑ + ∆2/ аt = 2*40 + 0,5*91 + 6,22/40 = 126,46.
Округляем до ближайшего четного числа Lt = 126 звеньев.
Уточняем межосевое расстояние по формуле
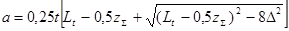 =
=
= 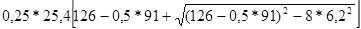 = 1010 мм.
= 1010 мм.
Для обеспечения свободного провисания следует уменьшить а на 0,4%, т.е. на 4 мм.
Размеры звездочек определяются по ГОСТ 591-69.
4.7 Муфты
Муфтами называются устройства, соединяющие два вала и передающие крутящий момент без изменения угловой скорости.
Муфты бывают: глухие; подвижные; сцепные (кулачковые и фрикционные); свободного хода (обгонные); упругие; центробежные; комбинированные и специальные.
Приведенная классификация муфт говорит об очень большом количестве самых разнообразных конструкций муфт.
Остановимся лишь на принципиальных отличиях муфт разных классов и рассмотрим конструктивные схемы различных муфт.
Глухие муфты.
 На рис. 4.21 приведены две схемы глухих муфт: втулочная (рис. 4.21, а); фланцевая (рис.4.21, б).
На рис. 4.21 приведены две схемы глухих муфт: втулочная (рис. 4.21, а); фланцевая (рис.4.21, б).
Основным достоинством этих муфт является простота
Рис. 4.21 конструкции. Существенный недостаток заключается в том, что муфта требует очень строгой соосности валов (0,002…0,05 мм). Эти муфты устанавливают на длинных гибких валопроводах или на консольных валах.
Муфты, в частности втулочная, могут выполнять роль предохранительных при условии, что штифты рассчитаны на номинальный крутящий момент, а все другие элементы конструкции на больший момент. При перегрузках штифт (штифты) срезается, но все другие элементы остаются целыми. Эту особенность используют в лодочных моторах, только там почему то штифт называют шпонкой.
Подвижные муфты
Подвижные муфты бывают: зубчатые; крестово-кулисные или с промежуточным сухарем; цепные; шариковые; муфты с гофрами и др. Эти муфты допускают осевое и угловое смещение валов. В частности, зубчатая муфта допускает осевое смещение валов до нескольких мм и угловое смещение до 0,50. Цепная муфта допускает радиальное смещение валов до 1,2 мм и угловое до 10 ( в специальных конструкциях – до 3…60).
 На рис. 4.22 показана муфта с промежуточным сухарем (аналогично устроена крестово-кулисная муфта). Такая муфта допускает все виды смещения валов. В процессе вращения валов сухарь перемещается по пазам в пределах несоосности валов.
На рис. 4.22 показана муфта с промежуточным сухарем (аналогично устроена крестово-кулисная муфта). Такая муфта допускает все виды смещения валов. В процессе вращения валов сухарь перемещается по пазам в пределах несоосности валов.
Рис. 4.22 Очевидно, что возникают силы трения. Для их уменьшения материалы пары полумуфта-сухарь выбирают с малым коэффициентом трения-скольжения.
Сцепные муфты
На рис. 4.23, а) показана сцепная кулачковая муфта.
 Профиль кулачков имеет форму трапеции (рис. 4.23, б). Результирующая сил N раскладывается на две составляющие: P – создает крутящий момент; Q – пытается раздвинуть полумуфты. Силе Q противостоит возвратная сила пружины S. Эта муфта может выполнять роль предохранительной. При перегрузках
Профиль кулачков имеет форму трапеции (рис. 4.23, б). Результирующая сил N раскладывается на две составляющие: P – создает крутящий момент; Q – пытается раздвинуть полумуфты. Силе Q противостоит возвратная сила пружины S. Эта муфта может выполнять роль предохранительной. При перегрузках
Q ≥ S. При этом полумуфты выходят из
Рис. 4.23 зацепления. Срабатывание предохранительной сцепной муфты сопровождается характерным треском. Если профиль кулачков прямоугольный, то Q = 0 и муфта не будет предохранительной.
 Более известны сцепные фрикционные муфты (устанавливаются в автомобилях). Схема такой муфты показана на рис. 4.24.
Более известны сцепные фрикционные муфты (устанавливаются в автомобилях). Схема такой муфты показана на рис. 4.24.
Передача крутящего момента в таких муфтах осуществляется за счет сил трения. Эта муфта так же
Рис. 4.24 является предохранительной.
При перегрузках фрикционные диски проскальзывают друг по другу.
Срабатывание муфты как предохранительной сопровождается характерным запахом. Говорят «горит сцепление».
Муфты свободного хода (обгонные) (рис. 4.25).
 Муфта передает крутящий момент только в одну сторону.
Муфта передает крутящий момент только в одну сторону.
Ведущий вал выполнен фасонным. В зазоры вставлены ролики и поджимаюшие пружинки. При вращении ведущего вала, ролики под действием сил трения и центробежных сил перемещаются по зазору и заклинивают ведущий и ведомый валы. Ведомый вал
Рис. 4.25 вращается вместе с ведущим. При остановке ведущего вала или при замедлении его вращения, ведомый вал, по инерции, продолжает вращаться (ω2 > ω1). Ролики перемещаются ведомым валом в больший зазор и расцепляют валы. Ведомый вал обгоняет ведущий.
С такими муфтами каждый из Вас находился рядом. Они установлены в каждом велосипеде.
Упругие муфты (рис. 4.26)
 Этот тип муфт устанавливается в приводах наиболее часто. Конструкций упругих муфт очень много, но принципиальная особенность одна. Она заключается в том, что между ведущим и ведомым валами устанавливаются упругие элементы (пружины, резина и др.). Характеристика упругих элементов обычно линейная (рис.4.26, б).
Этот тип муфт устанавливается в приводах наиболее часто. Конструкций упругих муфт очень много, но принципиальная особенность одна. Она заключается в том, что между ведущим и ведомым валами устанавливаются упругие элементы (пружины, резина и др.). Характеристика упругих элементов обычно линейная (рис.4.26, б).
Рис. 4.26 При резком запуске двигателя упругие элементы муфты первыми воспринимают на себя внезапно возникшую нагрузку.
Они сжимаются и передают эту нагрузку по нарастающей исполнительному механизму. Муфта гасит жесткий удар при пуске двигателя и дает механизму время на «пробуждение». Процесс можно сравнить с тем, что если бы Вас разбудил будильник или вылитое на Вас ведро воды. В процессе работы так же возможны колебания нагрузки. И в этих случаях упругая муфта сглаживает перепады нагрузки.
Центробежные муфты (рис. 4.27)
 Само название муфты характеризует ее принцип действия.
Само название муфты характеризует ее принцип действия.
На ведущем валу шарнирно закреплены сектора, на ободах которых установлены фрикционные накладки. При вращении ведущего вала центробежные силы раздвигают сектора и прижимают накладки к диску ведомого вала. Возникающие при этом силы трения создают крутящий момент. По такой же схеме устроены
Рис. 4.27 дисковые тормоза автомобилей, только раздвижение секторов (тормозных колодок) осуществляется не за счет центробежных сил, а с помощью гидравлики.
Кроме выше приведенных, существует еще много других муфт: порошковые; электромагнитные; пневматические и др.
4.8 Оси и валы
Оси служат для поддержания вращающихся вместе с ними или на них различных деталей машин и механизмов. Оси не передают крутящие моменты, поэтому рассчитываются только на изгиб по методике, изложенной в разделе 1.
Валы в отличие от осей предназначены для передачи крутящих моментов и поддержания вращающихся вместе с ними деталей машин. Валы воспринимают от закрепленных на них деталей соответствующие нагрузки, следовательно, работают одновременно на изгиб и кручение. Исключение составляют валы работающие только на кручение: карданные; гибкие.
Различают валы жесткие и гибкие (рис. 4.28). Жесткие валы в зависимости от конструкции могут быть: прямыми; кривошипными; коленчатыми; кулачковыми; эксцентриковыми. Прямые валы могут быть гладкими или ступенчатыми; сплошными или полыми.
 Жесткие валы изготавливают из стали с высокими механическими характеристиками и
Жесткие валы изготавливают из стали с высокими механическими характеристиками и
малой чувствительностью
Рис. 4.28 к концентрации напряжений.
Чаще применяется сталь 45, реже сталь 20, 30, 40, 50. Тяжелонагруженные валы изготавливают из легированных сталей марок 20Х, 40Х, 30ХГСА, 40ХН и др. Увеличение прочности и износостойкости валов достигается закалкой и отпуском до 41…51 НRС.
Расчет жестких валов на совместное действие изгиба с кручением рассмотрим на конкретном примере. Расчетная схема и эпюры изгибающих и крутящего момента приведены на рис.4.29.
 Дано: Т1 = 120 Н*м; Р = 3000 Н; Рr = 1100 Н; Ра = 530 Н; l = 90 мм; d = 80 мм. Материал вала сталь 40Х, термообработка – закалка + отпуск σВ = 980 МПа.
Дано: Т1 = 120 Н*м; Р = 3000 Н; Рr = 1100 Н; Ра = 530 Н; l = 90 мм; d = 80 мм. Материал вала сталь 40Х, термообработка – закалка + отпуск σВ = 980 МПа.
Решение:
Валы – это тяжелонагруженные детали, работающие в сложном динамическом режиме. Поэтому коэффициент запаса прочности принимается в пределах 4…10. В нашем случае примем n = 5. Тогда [σ] = σВ/ n = 980/5 =
= 196 МПа; [τ] = 0,5[σ] = 196/2 = 98 МПа.
Реакции опор в горизонтальной плоскости равны:
Rх1 = Rх2 = Р/2 = 3000/2 = 1500 Н.
Рис. 4.29
Реакции опор в вертикальной плоскости равны:
Ry1 = (Рr* l + Ра* d/2)/2 l = (1100*90 + 530*40)/180 = 668 Н.
Ry2 = (Рr* l - Ра* d/2)/2 l = (1100*90 - 530*40)/180 = 432 Н.
Максимальный изгибающий момент в горизонтальной плоскости равен:
Тy = Rх1* l = 1500*90 = 135*103 Н*мм = 135 Н*м.
Изгибающие моменты в вертикальной плоскости равны:
Тx1 = Ry1* l = 668*90 = 60,12*103 Н*мм = 60,12 Н*м;
Тx2 = Ry2* l = 432*90 = 38,88*103 Н*мм = 38,88 Н*м.
Ткр = Т1 = 120 Н*м.
Суммарный изгибающий момент равен:
Ти = √ Тх2 + Ту12 = √ 1352 + 60,122 = 148 Н*м.
Приведенный или эквивалентный момент вычисляют по третьей теории прочности:
Тэкв = √ Ти2 + Ткр2 = √1482 + 1202 = 190,5 Н*м.
Диаметр вала определяется по формуле
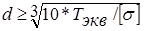 (4.42)
(4.42)
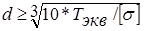 =
= 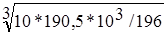 = 21,3 мм.
= 21,3 мм.
Ближайший больший стандартный диаметр 22 мм.
При сравнительно коротких валах и в курсовом проектировании валы рассчитывают только на кручение. При этом допустимое касательное напряжение принимают заниженным, на мой взгляд не обоснованно. Так в курсовом проектировании предлагается [τ] = 20…25 МПа.
Диаметр вала определяется по формуле
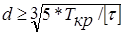 (4.43)
(4.43)
В нашем примере 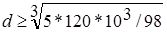 = 18,3 мм.
= 18,3 мм.
При [τ] = 25 МПа 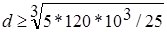 = 28,8 мм. Получили диаметр больший, чем при совместном действии изгиба с кручением, то есть допустимое напряжение явно занижено.
= 28,8 мм. Получили диаметр больший, чем при совместном действии изгиба с кручением, то есть допустимое напряжение явно занижено.
4.9 Подшипники качения
Подшипники качения состоят из наружного и внутреннего колец с дорожками качения; тел качения (шариков или роликов); сепаратора, разделяющего и направляющего шарики или ролики. В некоторых подшипниках отсутствует одно или оба кольца, а в других – сепаратор.
Достоинства подшипников качения: малые моменты сил трения и пусковые моменты, малый нагрев, незначительный расход смазочных материалов, простое обслуживание.
Недостатки подшипников качения: ограниченная способность воспринимать ударные и динамические нагрузки; большие габариты по диаметру (в сравнении с подшипниками скольжения).
В зависимости от направления нагрузки различают подшипники: радиальные, воспринимающие только радиальную или радиальную и некоторую осевую нагрузку; упорные, воспринимающие только осевую нагрузку; радиально-упорные и упорно-радиальные, способные воспринимать радиальную и осевую нагрузку одновременно.
По грузоподъемности (при одинаковом внутреннем диаметре) подшипники разделяются на серии: по радиальным габаритным размерам – сверхлегкие, особо легкие, легкие, средние, тяжелые; по ширине –узкие, нормальные, широкие, особо широкие.
Внутренние диаметры подшипников условно разделены на 3 диапазона: 1…9 мм; 10…17 мм; ≥ 20 мм.
На рис.4.30 показаны наиболее распространенные типы подшипников.
 Радиальный шариковый (рис.4.30 а) – воспринимает в основном радиальную нагрузку, но допускает и осевую нагрузку P ≤ 0,25R . Радиально-упорный шариковый (рис. 4.30, б) работает при радиальной и осевой нагрузке в соотношениии
Радиальный шариковый (рис.4.30 а) – воспринимает в основном радиальную нагрузку, но допускает и осевую нагрузку P ≤ 0,25R . Радиально-упорный шариковый (рис. 4.30, б) работает при радиальной и осевой нагрузке в соотношениии
Рис. 4.30 P ≤ 0,75R при α ≥ 260, где α – угол контакта
(α = 120; 240; 260; 350; 360). Шариковый упорный (рис. 4.30,в) воспринимает только осевую нагрузку. На рис. 4.30, г, д, е показаны роликовые подшипники. Грузоподъемность роликовых подшипников на 70…90% выше грузоподъемности шариковых подшипников, но они уступают шариковым по КПД ( трение больше) и по предельным скоростям вращения.
Роликовый радиальный с короткими цилиндрическими роликами
(рис. 4.30, г) и с длинными игольчатыми роликами (рис. 4.30, д) воспринимают только радиальную нагрузку. Роликовый конический радиально-упорный (рис. 4.30, е) воспринимает одновременно значительные радиальную и осевую нагрузки.
Подшипники маркируются номерами. Расшифровка номера производится справа налево. Первые две цифры (d ≥ 10 мм) или одна цифра (d = 1…9 мм) характеризуют внутренний диаметр подшипника; 3-я цифра или 2-я цифра (при d = 1…9 мм) указывает серию подшипника; 4-я цифра представляет тип подшипника. Цифр в номере подшипников может быть и больше 4-х. Цифры, начиная с 5-й, характеризуют конструктивные разновидности подшипников.
Примеры расшифровки подшипников по номерам.
№ 29 – d = 9 мм; серия легкая (цифра 2); радиальный шариковый (3-ей цифры нет или 0). № 36102 – d = 15 мм; серия особо легкая (цифра 1); шариковый радиально-упорный (цифра 6); угол контакта α = 120 (цифра 3).
№ 8308 – d = 40 мм; серия средняя (цифра 3); шариковый упорный (цифра 8).
№ 2505 – d = 25 мм; серия легкая широкая (цифра 5); роликовый радиальный с короткими цилиндрическими роликами (цифра 2). № 4074907 – d = 35 мм; серия сверхлегкая (цифра 9); роликовый радиальный с длинными игольчатыми роликами (цифра 4); остальные цифры – конструктивные разновидности.
№ 7612 – d = 60 мм; серия средняя широкая (цифра 6); роликовый конический радиально-упорный (цифра 7).
Для подшипников d ≥ 20 ммвнутренний диаметр определяется
d = 2-е правые цифры, умноженные на 5 (см. примеры).
В маркировке подшипников перед номером через дефис указывается класс точности (кроме 0). Классы точности подшипников мы рассматривали в разделе «Основы взаимозаменяемости».
Расчет подшипников качения
Подшипники рассчитываются на долговечность. Расчетная долговечность L в млн. оборотов или Lh в часах определяются по формулам:
L = (С/Рэ)m (4.44)
Lh = 106 L/(60n) (4.45)
Здесь С – динамическая грузоподъемность подшипника (принимается по каталогу подшипников); Рэ – эквивалентная нагрузка на подшипник;
n – частота вращения вала, об/мин.
Эквивалентная нагрузка Рэ для однорядных радиальных шарикоподшипников и радиально-упорных шарико- и роликоподшипников
Рэ = (XVFr + YFa)KбKт (4.46)
Для радиальных подшипников с короткими цилиндрическими роликами
Рэ = VFr KбKт (4.47)
Для упорных шариковых и роликовых подшипников
Рэ = Fа KбKт (4.48)
Здесь Х – коэффициент радиальной нагрузки; V – коэффициент, учитывающий вращение колец; при вращении внутреннего кольца V = 1,0 , наружного кольца V = 1,2; Fr – радиальная нагрузка, Н; Y – коэффициент осевой нагрузки;
Fa – осевая сила, Н; Kт – температурный коэффициент; Kб – коэффициент безопасности.
Коэффициенты Х и Y зависят от соотношения Fa/( V* Fr) и е – параметр осевого нагружения. Параметр е выбирается по таблицам и зависит от отношения Fa/С0, где С0 – статическая грузоподъемность (принимается по каталогу).
Для радиальных и радиально-упорных шариковых подшипников при
Fa/( V* Fr) ≤ е принимают Х = 1, Y = 0.
При Fa/( V* Fr) ≥ е Х и Y выбираются по таблицам, приведенным в каталогах подшипников и в литературе по деталям машин.
Долговечность подшипников должна соответствовать ресурсу изделия, но не меньше 5000 часов.
4.10 Резьбы: типы и обозначения
Резьбы бывают: метрическая; метрическая коническая; трубная цилиндрическая; трубная коническая; коническая дюймовая; трапецеидальная; упорная и специальные резьбы.
Резьба метрическая.
Резьба имеет треугольный профиль, с углом 600. Условная запись резьбы имеет вид:
М20 - 6g, где М – тип резьбы (метрическая); 20 – номинальный диаметр резьбы; 6g – поле допуска резьбы; 6 – степень точности ; g – основное отклонение резьбы болта (буква строчная).
Для резьб с нормальной длиной свинчивания (N) предусмотрены 3 класса точности с рекомендуемыми полями допусков гаек и болтов:
точный (5Н; 4h; 4g); средний (6H; 6G; 6h; 6g; 6d; 6e; 6f);
грубый ( 7H; 7G; 8h; 8g). При других длинах свинчивания болта и гайки
(S – малая длина свинчивания или L – большая длина свинчивания) рекомендуемые поля допусков по классам точности отличаются от приведенных выше. Подробнее смотри ГОСТ 16093-81.
Такая же резьба, только с мелким шагом: М20х1,5 - 6g (шаг 1,5 мм).
Предыдущая резьба, только левая: М20х1,5 LH - 6g.
Резьба двухзаходная : М20х3(Р1,5) LH - 6g. Здесь 3мм – ход винтовой линии; Р1,5 – шаг.
Гайка для болта с предыдущей резьбой: М20х3(Р1,5) LH – 6Н.
Резьба трубная цилиндрическая (применяется в сантехнике).
Профиль резьбы треугольный, с углом 550, поэтому шаг резьбы не совпадает с шагом метрической резьбы. Резьба обозначается в дюймах
(1 дюйм ≈ 25,4 мм). При этом в дюймах указывают не диаметр резьбы, а
условный проход трубы, то есть ≈ внутренний диаметр трубы.
Например: G 1/ 2 – А. Говорят: «резьба на пол дюйма», а про трубу - «труба на пол дюйма» или «труба на 15». А – степень точности резьбы. Предусмотрено всего две степени точности А и В; А точнее В.
Запись G 1¼ – В – читается – резьба на дюйм с четвертью.
Резьбы конические.
Конические резьбы применяются для соединения трубопроводов, штуцеров с сосудами высокого давления, сливных пробок с емкостями без применения дополнительных уплотнений. Эти резьбы самоуплотняемые. Угол конуса не большой ≈ 3,50. Конические резьбы имеют 3 типа исполнения:
метрическая коническая (угол профиля 600); трубная коническая (угол профиля 550); коническая дюймовая (угол профиля 600).
Условные обозначения резьб следующие:
МК20х1,5 ГОСТ 25229-82 – резьба метрическая коническая, диаметр 20мм, шаг 1,5мм, допуски по ГОСТ 25229-82.
R 1½ - наружная трубная коническая резьба полтора дюйма;
Rс 1½ - внутренняя трубная коническая резьба полтора дюйма.
В обоих случаях 1½ - условный проход трубы в дюймах.
К3/8" – коническая дюймовая резьба с условным проходом 3/8" .
Резьба трапецеидальная.
Такие резьбы применяются в ходовых винтах станков и станочных приспособлений. Профиль резьбы трапецеидальный с углом 300.
Tr32х6(Р2) LH – 8е – винт, резьба трапецеидальная, диаметр 32мм, трехзаходная, шаг 2мм, левая, 8-я степень точности , основное отклонение резьбы по е.
Гайка для этого винта: Tr32х6(Р2) LH – 8Н.
Резьба упорная.
Эти резьбы применяются в винтовых домкратах большой грузоподъемности, в креплениях крюков грузоподъемных механизмов, там, где действует большая односторонняя нагрузка. Профиль резьбы пилообразнай: передний угол – 30; задний угол – 300.
Условная запись резьбы имеет вид:
S80х12 - 7h – винт, резьба упорная, диаметр 80мм, шаг 12мм, 7-я степень точности, основное отклонение резьбы по h.
4.11 Болтовые соединения
 Людям, работающим с техникой, постоянно приходится иметь дело с болтовыми соединениями. Очень часто возникают вопросы: как надо (на сколько надо) закручивать болт или гайку, чтобы не срезать или не смять резьбу; не разорвать болт; не свернуть головку болта; предотвратить относительное смещение стягиваемых деталей и др. Предварительные ответы на эти вопросы могут дать расчеты болтового соединения, а окончательные – собственный практиче-
Людям, работающим с техникой, постоянно приходится иметь дело с болтовыми соединениями. Очень часто возникают вопросы: как надо (на сколько надо) закручивать болт или гайку, чтобы не срезать или не смять резьбу; не разорвать болт; не свернуть головку болта; предотвратить относительное смещение стягиваемых деталей и др. Предварительные ответы на эти вопросы могут дать расчеты болтового соединения, а окончательные – собственный практиче-
Рис. 4.31 ский опыт.
Схема болтового соединения показана на рис. 4.31.
На рисунке обозначено: Рзав – сила завинчивания (осевая сила болта);
Рр – сила руки, прикладываемая к ключу; Lкл – длина ключа; F – внешние силы; d – наружный диаметр резьбы; Н – высота гайки. Кроме того нам понадобятся: d1 – внутренний диаметр резьбы; d2 – средний диаметр резьбы;
р – шаг резьбы. d1 ≈ d – р; d2 ≈ d – р/2.
Момент завинчивания Тзав = Рр* Lкл расходуется на создание Рзав при перемещении болта по гайке и на преодоление сил трения в резьбе и на торце гайки. Трением на торце гайки зачастую пренебрегают.
Следовательно можно записать
Рзав*0,5 d2*tg(ψ + φ) = Рр* Lкл (4.49)
Здесь ψ = arctq(p/πd2) – угол подъема резьбы; φ = arctq(f') – приведенный угол трения в резьбе. В резьбовом соединении (сталь-сталь) коэффициент трения скольжения обычно принимают f = 0,15, однако, учитывают профиль резьбы. Для метрической резьбы приведенный коэффициент трения f' = 1,15 f = 0,17, соответственно, приведенный угол трения φ = 9,650. Для трапецеидальной резьбы f' = 1,04 f = 0,156, соответственно, приведенный угол трения φ = 8,870.
Для практических расчетов из формулы (4.49) Вы можете выразить любой из 3-х параметров (Рзав; Рр; Lкл) при известных остальных параметрах.
Рассмотрим методику расчета болтовых соединений при различных постановках задачи.
Расчет болтов на растяжение.
Условие прочности болта имеет вид
σ = Рзав/(πd12/4) ≤ [σ] (4.50)
Из формулы (4.50) Вы можете определить допустимую для данного болта осевую силу Рзав, а затем Рр при заданной Lкл или наоборот. Так же можете подобрать диаметр болта при заданной Рзав, после преобразований получим
d1 ≥ 1,13√ Рзав/[σ] (4.51)
Для учета совместного действия растяжения и кручения болта рекомендуется диаметр болта определять по формуле
d1 ≥ 1,3√ Рзав/[σ] (4.52)
Расчет резьбы на срез.
Условие прочности имеет вид
τ = Рзав/( πd1*Н*k*km) ≤ [τ] (4.53)
Здесь k – коэффициент полноты резьбы, для треугольной резьбы k ≈ 0,87, для трапецеидальной резьбы k ≈ 0,65; km – коэффициент неравномерности нагрузки по виткам резьбы (km = 0,55…0,75) , большие значения для резьб с крупным шагом.
Расчет резьбы на смятие.
Условие прочности на смятие резьбы имеет вид
σ см = Рзав/(πd2*h*z) ≤ [σ]см (4.54)
Здесь h = р/1 – высота витка резьбы; z = Н/р – число витков резьбы в зоне смятия.
Не сложно подобрать диаметр резьбы из условия прочности на срез или на смятие при принятых высоте гайки (Н) и шаге резьбы (р) или подобрать высоту гайки для известного болта. Эти преобразования формул (4.53) и (4.54) Вам предлагается выполнить самостоятельно.
Расчет болтов на предотвращение относительного смещения деталей.
На две, стянутых болтом и гайкой, детали действуют силы F. Задача – предотвратить смещение деталей. От относительного смещения детали удерживает сила трения. Сила Рзав должна быть Рзав ≥ s*F/f, где s = 1,5…2 – коэффициент запаса сцепления; f – коэффициент трения материалов деталей. Для сухих стальных или чугунных деталей f = 0,15…0,2; для необработанных поверхностей в металлических конструкциях f = 0,3.
После определения необходимой Рзав, по формуле (4.52) находим требуемый диаметр болта. При этом допустимое напряжение принимают
[σ] = 0,6 σт.
Если болт установлен без зазора или стык деталей не достаточно плотный, то болт рассчитывается на срез, как обычная односрезная заклепка.
Резьбовые соединения могут быть подвержены и более сложным видам нагружения. Решение таких задач можете найти в [8].
4.12 Выбор электродвигателя и кинематический расчет привода
 В инженерной практике достаточно часто возникает необходимость скомпоновать привод какого-нибудь исполнительного механизма, а затем произвести проверочные или проектировочные расчеты отдельных элементов привода. Рассмотрим первый этап этой работы. Предположим, что Вам потребовался привод, состоящий из электродвигателя (М), клиноременной передачи, цилиндрического редуктора и червячного редуктора.
В инженерной практике достаточно часто возникает необходимость скомпоновать привод какого-нибудь исполнительного механизма, а затем произвести проверочные или проектировочные расчеты отдельных элементов привода. Рассмотрим первый этап этой работы. Предположим, что Вам потребовался привод, состоящий из электродвигателя (М), клиноременной передачи, цилиндрического редуктора и червячного редуктора.
Рис. 4.32 Схема привода показана на рис. 4.32.
Дано: NВВ = 5 кВт; nВВ = 5 об\мин
(мощность и обороты на ведомом валу).
Решение.
1. Выбор электродвигателя по оборотам.
n д = nВВ*u общ. u общ = u кр* u р* u чр
Предположим, имеется в наличии червячный редуктор с u чр = 20 и
цилиндрический редуктор с u р = 4. Принимаем предварительно u кр = 3.
Тогда u общ = u кр* u р* u чр = 3*4*20 = 240. Соответственно,
n д = nВВ*u общ = 5*240 = 1200 об/мин. Двигателя с такими оборотами нет. Есть электродвигатели с числом оборотов в минуту:
1000 об/мин; 1500 об/мин. Ближе двигатель на 1000 об/мин.
Уточняем u общ = n д/ nВВ = 1000/5 = 200.
Уточняем u кр = u общ/( u р* u чр) = 200/80 = 2,5.
Таким образом, мы подобрали электродвигатель по оборотам и определили передаточные отношения на каждой ступени и привода в целом.
2. Выбор электродвигателя по мощности.
Nд = NВВ/ηобщ, где ηобщ – общий КПД привода.
ηобщ = ηо4* ηкр* ηр* ηчр = 0,994*0,96*0,97*0,8 = 0,7156.
Здесь ηо = 0,99…0,995 – КПД опор каждого вала; ηкр = 0,95…0,97 – КПД клиноременной передачи; ηр = 0,97…0,98 – КПД цилиндрического редуктора;
ηчр = 0,80…0,85 – КПД червячного редуктора при двухзаходном червяке
( при однозаходном червяке ηчр = 0,70…0,75). Однозаходный червяк может быть только при u чр ≥ 26.
Nд = NВВ/ηобщ = 5/0,7156 = 6,99 кВт. Ближайший больший электродвигатель имеет мощность Nд = 7,5 кВт.
Марка электродвигателя 4А132М6.
Для дальнейшего расчета элементов привода Вам потребуются параметры на всех валах привода: мощность – N, Вт; число оборотов – n, об/мин; угловая скорость – ω, с-1; крутящий момент – Т, Н*м. Составим таблицу этих параметров (таблица 10.4).
Таблица 10.4
| № вала | N, Вт | n, об/мин | ω, с-1 | Т, Н*м |
| 104,7 | 66,7 | |||
| 41,9 | ||||
| 10,5 | ||||
| 10,5 | ||||
| 0,52 | ||||
| вв | 0,52 |
Известно: ω = π* n/30; N = Т* ω;
Т = N/ ω.
Если получены 2 столбца таблицы, то два других просто вычисляются. Двигаясь от ведомого вала к ведущему, вычисляем мощности по формулам:
N5 = NВВ/ ηо; N4 = N5/( ηо* ηчр);
N3 = N4/ ηо;
N2 = N3/( ηо* ηр); N1 = N2/ ηкр.
Аналогично по оборотам.
n 5 = nВВ; n 4 = n 5* u чр; n 3 = n 4; n 2 = n 3* u р; n 1 = n 2* u кр = n д.
Теперь Вы можете рассчитывать все элементы привода по методикам, изложенным выше.
Литература
1. Анурьев В.К. Справочник конструктора-машиностроителя в 3-х томах. – М.:
Машино строение, 1980.
2. Чернавский С.А. и др. Курсовое проектирование деталей машин: Учебное пособие. – М.: Машиностроение, 1988. – 416 с.
3. Гузенков П.Г. Детали машин. 4-е изд. – М.: Высшая школа, 1986. – 360 с.
4. Решетов Д.Н. Детали машин. 4-е изд. – М.: Машиностроение, 1989. – 496 с.
5. Иванов М.Н. Детали машин. 5-е изд. – М.: Высшая школа, 1991. – 383 с.
6. Перель Л.Я. Подшипники качения. – М.: Машиностроение, 1983. – 588 с.
7. Поляков В.С., Барбаш И.Д. Муфты. Конструкции и расчет. 4-е изд. – Л.: Машиностроение, 1973. – 336 с.
8. Биргер И.А., Иосилевич Г.Б. Резьбовые и фланцевые соединения. – М.: Машиностроение, 1990. – 368 с.
Содержание
I. Основы сопротивления материалов
1.1 Внешние силы (нагрузки)
1.2 Метод сечений
1.3 Напряжения
1.4 Диаграмма растяжения
1.5 Деформация растяжения и сжатия
1.6 Деформация сдвига (среза)
1.7 Деформация смятия
1.8 Геометрические характеристики сечений
1.9 Деформация кручения
1.10 Деформация изгиба
1.11 Определение перемещений при изгибе по способу Верещагина
1.12 Устойчивость сжатых стержней
I I. Основы взаимозаменяемости
I I I. Основы теории механизмов и машин (ТММ)
3.1 Структурный анализ механизмов
3.1.1 Основные понятия и определения
3.1.2 Степень подвижности механизма
3.1.3 Замена высших кинематических пар низшими
3.1.4 Структурный синтез и анализ механизмов
3.2 Кинематический анализ механизмов
3.2.1 Определение положений и перемещений звеньев механизма
3.2.2 Определение скоростей и ускорений точек и звеньев механизма
IV. Детали машин
4.1 Зубчатые передачи
4.1.1 Элементы зубчатых колес
4.1.2 Передаточное отношение, передаточное число
4.1.3 Силы в зацеплении цилиндрических зубчатых колес
4.1.4 Прочностной расчет цилиндрических зубчатых передач
4.1.4.1 Расчет зубьев на контактную прочность
4.1.4.2 Расчет зубьев на изгиб
4.1.5 Точность зубчатых передач
4.1.6 Способы (методы) нарезания зубьев
4.1.7 Передачи коническими зубчатыми колесами
4.1.8 Пример выполнения чертежа зубчатого колеса
4.2 Трение
4.3 Червячные передачи
4.4 Фрикционные передачи
4.5 Ременные передачи
4.5.1 Плоскоременные передачи
4.5.2 Клиноременные передачи
4.6 Цепные передачи
4.7 Муфты
4.8 Оси и валы
4.9 Подшипники качения
4.10 Резьбы: типы и обозначения
4.11 Болтовые соединения
4.12 Выбор электродвигателя и кинематический расчет привода
Дата добавления: 2015-02-05; просмотров: 1527;
