Нормальные углы и конусности
Анализ конфигурации деталей машин и приборов показывает, что достаточно часто их поверхности располагаются под некоторым углом, отличным от прямого. В таком случае на расположение элементов деталей назначают угловые размеры с соответствующими допусками.
Угловые элементы деталей можно условно разделить на элементы с углами общего назначения и со специальными углами, размеры которых связаны расчетными зависимостями с другими принятыми линейными и угловыми размерами в силу специфических эксплуатационных или технологических требований.
С целью разумного ограничения номенклатуры углов первой группы, к которой относятся конструктивные наклонные поверхности с произвольными уклонами, скосы, фаски и др. ГОСТ 8908–81 устанавливает три ряда нормальных углов, причем каждый последующий ряд не поглощает предыдущие (таблица 23). В соответствии с принципом предпочтительности первый ряд имеет приоритет перед вторым, второй перед третьим.
Термины и определения, относящиеся к поверхностям и элементам деталей, имеющим угловые элементы, установлены ГОСТ 25548 – 82 .
Под прямой круговой конической поверхностью (конической поверхностью или конусом) понимают поверхность вращения, образованную прямой образующей, вращающейся относительно оси и пересекающей ее.
Таблица 23
Ряды нормальных углов по ГОСТ 8908
| Ряд1 | Ряд 2 | Ряд 3 | Ряд 1 | Ряд 2 | Ряд 3 | Ряд 1 | Ряд 2 | Ряд 3 |
| 0° | 10° | 70° | ||||||
| 0°15' | 12° | 75° | ||||||
| 0°30' | 15° | 80° | ||||||
| 0°45' | 18° | 85° | ||||||
| 1° | 20° | 90° | ||||||
| 1°30' | 22° | 100° | ||||||
| 2° | 25° | 110° | ||||||
| 2°30' | 30° | 120° | ||||||
| 3° | 35° | 135° | ||||||
| 4° | 40° | 150° | ||||||
| 5° | 45° | 165° | ||||||
| 6° | 50° | 180° | ||||||
| 7° | 55° | 270° | ||||||
| 8° | 60° | 360° | ||||||
| 9° | 65° |
Конус – обобщенный термин, под которым в зависимости от конкретных условий понимают коническую поверхность, коническую деталь или конический элемент детали.
В деталях конические поверхности часто стыкуются с цилиндрическими поверхностями на продолжении той же оси и имеют вид усеченного конуса с большим и меньшим основаниями.
Под основаниями конуса понимают круговые сечения, образованные пересечением конической поверхности с плоскостями перпендикулярными оси и ограничивающими его в осевом направлении.
Основной плоскостью называют плоскость поперечного сечения конуса, в котором задается номинальный диаметр конуса.
Базовой плоскостью является плоскость, перпендикулярная оси конуса и служащая для определения осевого положения основной плоскости или осевого положения данного конуса относительно сопрягаемого с ним конуса.Базовая плоскость может совпадать или не совпадатьс основной.
Элементы конусов обозначаются следующим образом (рис.3.92). Диаметры поперечных сечений конусов: большого основания – D; малого – d; заданного сечения (в котором задан допуск) – DS, произвольно расположенного сечения – dх. Угол конуса обозначают α, угол уклона конуса α/2. Параметры наружных конусов помечают индексом е, внутренних – i.
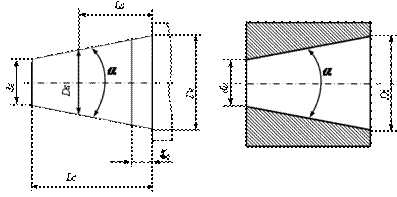
Рис. 3.92. Основные параметры конусов и конического соединения
Угол уклона конуса α/2 связан с размерами D, d и L следующим соотношением:
C = (D – d)/L = 2tg(α/2),
или
С/2 = 0,5(D – d)/L = tg(α/2),
где С – конусность;
С/2 – уклон i.
Приведенные взаимосвязи следует учитывать при назначении угловых и линейных размеров конусов и допусков этих размеров.
При необходимости различения параметров конических соединений, наружных и внутренних конусов в обозначениях параметров наружных конусов используют индексы e, параметров внутренних конусов индексы i, а для параметров конических соединений – р.
Обозначение длины конуса – L, длины конического соединения – Lр, осевое расстояние от большего основания конуса до заданного сечения – LS, до произвольно расположенного сечения – Lх. Расстояние между основной и базовой плоскостями конуса (базорасстояние конуса) обозначают ze или zi, а базорасстояние конического соединения – zp.
Усеченный конус (наружный и внутренний) характеризуется диаметром большого основания D, диаметром малого основания d, длиной конуса L и углом конуса α.
Дата добавления: 2015-02-05; просмотров: 1274;
