Пример расчета. На лесной территории площадью 1000 га с хвойными насаждениями (сосна) установилась сухая погода с температурой в 12 часов дня =25 °С

На лесной территории площадью 1000 га с хвойными насаждениями (сосна) установилась сухая погода с температурой в 12 часов дня 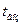=25 °С. Принимая , что точка росы равная =21 °С, определить, через сколько дней после установления жаркой погоды возникает пожароопасная обстановка.

Определить последствия пожара через 24 часа после его возникновения, если начальный периметр низового пожара =10000 м, а скорость ветра – 4 м/с.

Решение

1. Из формулы (6.2) с учетом данных таблиц 6.2 найдем количество дней, через которое возникает пожароопасная обстановка при условии, что в эти дни 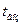, =const

Для этого перепишем выражение (6.2)

K= n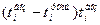

и решим полученное уравнение относительно n:

n= .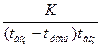

Тогда по условиям примера (К=550 - сосняки)

N=550/[(25-21)25]=5,5 (дня).

2. Учитывая, что сосняки относятся к первой группе по загораемости, для скорости ветра =4м/с и II класса пожарной опасности (300<K<1000 (см. табл.6.2)), по графику на рис 6.1, а определяем , что линейная скорость фронта низового пожара равна 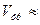90 м/ч, а линейные скорости распространения флангов 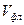и тыла 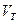определим по графикам на рис 6.1, б и 6.1, в:

20 (м/ч), 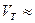10 (м/ч).

3. Приращение периметра ∆П за 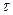=24 часа найдем по формуле (6.3)

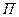∆ = 7100 (м).

4. Периметр пожара через 24 часа после загорания по формуле (6.4) будет равен

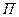=10000+7100=17100 (м).

5. Площадь пожара через 24 часа его после начала будет равна (формула 6.5)

S= 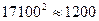(га),

т.е. пожар достигнет границ леса до окончания суток.

6. Определим время, за которое пожар охватит весь лесной массив площадью =1000 га, используя формулы (6.3) – (6.5), приняв S= :

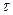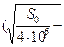
= )/(3,3 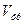)= 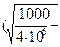10000)/( 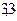120)=19,5 (ч).

7. Согласно табл. 6.3, в случае возникновения верхового устойчивого пожара 50 % леса окажется непригодной к реализации.