ПРОГНОЗИРОВАНИЕ ВЕРОЯТНОСТИ НАСТУПЛЕНИЯ ЧРЕЗВЫЧАЙНЫХ СИТУАЦИЙ
Количественные характеристики риска чрезвычайных ситуаций 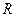 представляет собой прогнозирование вероятности её наступления
представляет собой прогнозирование вероятности её наступления 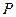 на величину ожидаемого ущерба У:
на величину ожидаемого ущерба У:
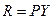 . (1.1)
. (1.1)
Вероятности наступления очередной ЧС зависит о времени ожидания
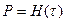 , (1.2)
, (1.2)
где τ> 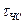 - время ожидания,
- время ожидания, 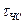 - продолжительность протекания самой ЧС,
- продолжительность протекания самой ЧС, 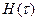 - функция риска. Функция риска является интегральной функцией распределения непрерывной случайной величины, Т-времени ожидания следующей ЧС, поэтому
- функция риска. Функция риска является интегральной функцией распределения непрерывной случайной величины, Т-времени ожидания следующей ЧС, поэтому
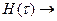 0 при
0 при 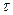
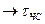 ;
;
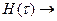 0 при
0 при 
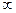 . (1.3)
. (1.3)
Для представления функции риска чаще всего используют показательную и степенную функцию:
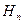
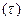 =1-exp-
=1-exp- 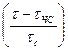 ; (1.4)
; (1.4)

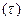 =1-
=1- 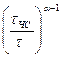 , (1.5)
, (1.5)
где 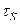 - средняя продолжительность чрезвычайной ситуации.
- средняя продолжительность чрезвычайной ситуации.
Функции риска (1.4) соответствует простейшему пуассонову потоку ЧС и быстро достигает насыщения, т.е. значения, близкого к единице. Функция риска (1.5) стремится к единице более медленно и характерна для последовательности редких катастрофических событий.
Параметры функций риска 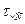 и
и 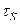 определяются путём статистической обработки вариационного ряда эмпирических значений интервалов между смежными ЧС.
определяются путём статистической обработки вариационного ряда эмпирических значений интервалов между смежными ЧС.
Для этого диапазоны изменения 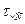 и
и 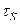 необходимо разбить на одинаковые частичные интервалы и подсчитать частоты значений этих величин
необходимо разбить на одинаковые частичные интервалы и подсчитать частоты значений этих величин 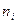 , попадающих в каждый интервал.
, попадающих в каждый интервал.
Каждому частичному интервалу ставится в соответствие значение 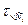 и
и 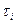 , равные среднему арифметическому концов этих интервалов. Относительные частоты значений
, равные среднему арифметическому концов этих интервалов. Относительные частоты значений 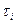 определяются по формуле
определяются по формуле
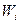 =
= 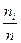 , (1.6)
, (1.6)
Где, 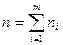 - объём выборки, m - число частичных интервалов. По относительным частотам периодов ожидания ЧС
- объём выборки, m - число частичных интервалов. По относительным частотам периодов ожидания ЧС 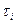 вычисляются значения эмпирической функции риска:
вычисляются значения эмпирической функции риска:
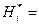
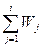 . (1.7)
. (1.7)
В качестве значений параметров 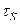 и
и 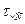 берутся их выборочные точечные оценки:
берутся их выборочные точечные оценки:
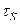 =
=  =
= 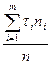 ; (1.8)
; (1.8)
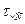 =
= 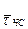 =
= 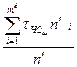 . (1.9)
. (1.9)
Параметр 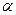 Функции риска (1,5) определяется по эмпирическим данным методом наименьших квадратов
Функции риска (1,5) определяется по эмпирическим данным методом наименьших квадратов
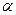 =1+
=1+ 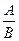 , (1.10)
, (1.10)
где: A=  (1.11)
(1.11)
B= 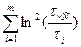 (1.12)
(1.12)
Более точно соответствует опытным данным функция риска, минимизирующая сумму квадратов разностей её расчётных и эмпирических значений:
S= 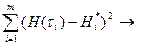 min. (1.13)
min. (1.13)
В формуле риска (1) входит вероятность наступления ЧС за единицу времени, обычно в течении года. Эта вероятность может быть найдена с помощью функции риска:
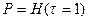 . (1.14)
. (1.14)
Дата добавления: 2015-02-05; просмотров: 1245;
