Разработка решений в условиях неопределенности и риска

Важнейшими факторами принятия решения могут быть названы информационные условия и их неопределенность. Известно определение Норберта Винера, в соответствии с которым информацией считаются данные, снижающие неопределенность в знаниях об объекте управления, среде.

Возможны несколько вариантов структурирования информации, используемой при разработке управленческих решений

Условия, в которых осуществляется прогнозирование и планирование. по степени определенности разделяются на детерминированные (определенные), случайные, неопределенные.

Детерминированные или определенные условия имеют место тогда, когда точно известен результат каждого из альтернативных вариантов выбора. Такая ситуация относительно редка.

Чаще в результате анализа факторов, влияющих на параметры объекта прогнозирования, приходят к выводу, что в условиях конкретной задачи все или часть параметров можно считать детерминированными. При этом считается, что существует лишь один вариант значения или изменения параметров.

Случайные условия имеют место тогда, когда представляется возможным определить вероятность появления каждого результата.

Вероятность определяется как степень возможности свершения данного события и изменяется от 0 до 1. Вероятность появления события можно оценить как частоту его появления на практике или при фиктивном разыгрывании, моделировании ситуации. Кроме этого вероятность может быть оценена экспертным путем.

События образуют полную группу, если сумма вероятностей всех альтернативных событий равна единице.

Неопределенные условия имеют место тогда, когда невозможно оценить вероятность потенциальных результатов. Это может иметь место при противодействии разумного противника или, когда требующие учета факторы настолько новы, что насчет них невозможно получить достаточно информации.

С другой стороны, по характеру отражения свойств вся имеющаяся информация об объекте прогнозирования может быть отнесена к следующим трем видам:

1) подсознательная или интуитивная (неосознанная);

2) предметное описание объекта;

3) формальные статистические данные.

При принятии решений используют все названные виды информации. Степень осведомленности об объекте определяется как абсолютным количеством информации каждого вида, так и соотношением названных видов информации.

Источником подсознательной информации могут выступать: опыт предыдущих поколений, благоприобретенный опыт, знания, полученные в процессе обучения и т.п. Воображение позволяет преобразовать эту информацию в более или менее формализованный качественный или количественный результат прогноза. Это используется при экспертном прогнозировании. В результате может быть получен качественный (хуже, лучше; больше, меньше и т.п.) или количественный прогноз, план.

Предметная информация – это описание процесса или состояния объекта дается естественным языком. Предметное описание объекта прогнозирования позволяет получить результат прогноза с использованием формальных методов математической логики и логики предложений. Результат прогнозирования может иметь только качественный характер.

Формальные статистические данные получают на этапе ретроспекции при анализе объекта прогнозирования или, используя данные официальной статистики. Результатом прогнозирования-планирования на основе этих данных будут количественные оценки.

Формальные статистические данные позволяют разрабатывать и проверять статистические гипотезы об адекватности прогнозных моделей, которые используют для получения прогнозов.

По степени достоверности знания делятся на достоверные (знания, полученные из официальных источников), знания относительной достоверности (полученные из случайных источников), знания с возможным умышленным искажением информации. Вопросы тайны, конфиденциальности, дезинформации при разработке управленческих решений обсуждаются в соответствующем параграфе главы 4.

Часть условий при разработке решения всегда неопределенна, поэтому практически все решения принимаются в условиях некоторой неопределенности. Но картина становится принципиально иной тогда, когда неопределенно большинство важнейших исходных данных.

"Неопределенными могут быть как условия выполнения операции, так и сознательные действия противников или других лиц, от которых зависит успех операции. Кроме того, неопределенность в той или другой степени может относиться также к целям (задачам) операции, успех которой не всегда может быть исчерпывающим образом охарактеризован одним единственным числом – показателем эффективности.

Разумеется, когда речь идет о неопределенности в каком-то смысле ситуации, то рекомендации, вытекающие из научного исследования, не могут быть столь же четкими и однозначными, как в случаях полной определенности. Однако и при отсутствии полной определенности количественный анализ ситуации все же может принести пользу и помочь при выборе решения. Разработаны специальные математические методы, предназначенные для обоснования решений в условиях неопределенности. В некоторых наиболее простых случаях эти методы дают возможность фактически найти и выбрать оптимальное решение.

В более сложных случаях эти методы доставляют вспомогательный материал, позволяющий глубже разобраться в сложной ситуации и оценить каждое из возможных решений с различных (иногда противоречивых) точек зрения, взвесить его преимущества и недостатки и, в конечном счете, принять решение, если не единственно правильное, то по крайней мере до конца продуманное.

Необходимо учитывать, что при выборе решения в условиях неопределенности всегда неизбежен элемент произвола, а значит, и риска. Недостаточность информации всегда опасна, и за нее приходится платить. Однако в условиях сложной ситуации всегда полезно представить варианты решения и их возможные последствия в такой форме, чтобы сделать произвол выбора менее грубым, а риск минимальным".

Как отмечалось, риск может быть снижен применением специальных приемов при разработке и принятии решений финансового менеджмента.

Задачами о принятии решений в условиях неопределенности занимает теория игр и статистических решений.

Перечислим предмет и основные понятия теории игр. Теория игр – это математическая теория конфликтных ситуаций. Задача этой теории – выработка рекомендаций по рациональному образу действий участников конфликта. При этом строят упрощенную модель конфликтной ситуации, называемую игрой. Под "игрой" понимают мероприятие, состоящее из ряда действий или "ходов". От реальной конфликтной ситуации игра отличается тем, что ведется по вполне определенным правилам. Стороны, участвующие в конфликте, называют "игроками", исход конфликта – "выигрышем" и т.д.

Если в игре сталкиваются интересы двух сторон, то игра называется парной, если сторон больше – множественной. Множественная игра с двумя постоянными коалициями обращает игру в парную. Наибольшее практическое значение имеют парные игры.

Для обеспечения возможности математического анализа игры должны быть:

1) правила игры;

2) система условий, регламентирующая:

· возможные варианты действий игроков;

· объем информации каждой стороны о поведении другой;

· результат (исход) игры, к которому приводит каждая данная совокупность ходов.

Игра называется игрой с нулевой суммой, если один игрок выигрывает ровно столько, сколько проигрывает другой, то есть сумма выигрышей равна нулю. В игре с нулевой суммой интересы противников прямо противоположны. Ниже описываются только такие игры.

Обозначим буквой а выигрыш игрока А, а буквой b – выигрыш игрока B в игре с нулевой суммой.

Так как: а = -b , то при анализе такой игры нет необходимости рассматривать оба эти числа, а достаточно рассматривать выигрыш одного из игроков; пусть это будет, скажем, игрок А. Условимся в дальнейшем называть "мы" сторону А, а сторону В – "противник".

Развитие игры во времени мы будем представлять состоящим из ряда последовательных этапов или "ходов".

Ходом в теории игр называют выбор одного из предусмотренных правилами игры действий и его осуществление. Ходы бывают личные и случайные.

Личным ходом называется сознательный выбор игроком одного из возможных вариантов действий и его осуществление. Случайным ходом называют выбор из ряда возможностей, осуществляемый не игроком, а каким-либо механизмом случайного выбора (например, бросанием монеты и др.). Для каждого случайного хода правила игры определяют распределение вероятностей возможных исходов.

Теория игр занимается анализом только тех игр, которые содержат личные ходы. Такие игры строятся на основании стратегий игрока.

Стратегией игрока называют совокупность правил, определяющих выбор варианта действий при каждом личном ходе этого игрока в зависимости от ситуации, сложившейся в ходе игры. В зависимости от числа возможных стратегий игры делятся на "конечные" и "бесконечные".

Игра называется конечной, если у каждого игрока имеется только конечное число стратегий, и бесконечной, если хотя бы у одного из игроков имеется бесконечное число стратегий.

Оптимальной стратегией игрока называется такая стратегия, которая при многократном повторении игры обеспечивает данному игроку максимально возможный средний выигрыш (или, что то же самое, минимально возможный средний проигрыш). При выборе оптимальной стратегии основой рассуждении является предположение, что противник по меньшей мере так же разумен, как и мы сами, и делает все для того, чтобы помешать нам добиться своей цели.

В теории игр не учитываются неизбежные в каждой конфликтной ситуации:

1) просчеты и ошибки игроков;

2) риск и азарт.

Кроме того важнейшим из ограничений математической теории игр является то. что выигрыш искусственно сводится к одному единственному числу (реально – это некоторый набор параметров эффекта: завоевание большей доли рынка, рост престижа марки и т.д.). Стратегия, оптимальная по одному показателю, необязательно будет оптимальной по другим.

Модель игры. Рассматривают конечную игру, в которой игрок А имеет m стратегий, а игрок В имеет n стратегий. Такая игра называется игрой m х n. Стратегии, соответственно, обозначим: A₁, A₂, ..., A_m – для игрока A; B₁, B₂, ..., B_n – для игрока В. Если игра состоит только из личных ходов, то выбор стратегий A_i и B_j игроками однозначно определяет исход игры – наш выигрыш а_ij. Если известны a_ij для всех сочетаний стратегий, то они образуют платежную матрицу размером m х n, где: m – число строк матрицы, а n – число его столбцов.

Если игра содержит кроме личных ходов и случайные ходы, то выигрыш при паре стратегий A_i и B_j есть величина случайная, зависящая от исходов всех случайных ходов. В этом случае естественной оценкой возможного выигрыша является математическое ожидание случайного выигрыша.

Нижняя и верхняя цена игры. Поставим задачу: определить наилучшую среди наших стратегий A₁, A₂ , ..., A_m. Условимся рассматривать только чистые стратегии. Затем проанализируем последовательно каждую из них от A₁ до A_m. Выбирая A_i, мы должны рассчитывать, что противник ответит на нее той из стратегий B_j, для которой наш выигрыш минимален. Найдем минимальное из чисел а_ij в i-той строке и обозначим его a_i:

.

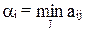Естественно, что осторожный игрок должен выбрать ту стратегию, для которой число a_i максимально. Обозначим это максимальное значение a:

,

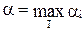а принимая во внимание формулу для a_i, можно записать:

.

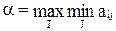Величина a называется нижней ценой игры, максиминным выигрышем или максимином. Соответствующая стратегия называется максиминной стратегией.

Очевидно, что аналогичное рассуждение можно провести и за сторону В. Эта сторона заинтересована в том, чтобы обратить наш выигрыш в минимум, то есть максимизировать свой выигрыш. Поэтому будут выделены максимальные значения выигрыша по столбцам:

.

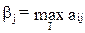Затем ищут минимальное значение b_j:

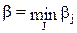или .

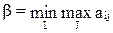Величина b называется верхней ценой игры, иначе – минимаксным выигрышем или минимаксом. Соответствующая выигрышу b стратегия называется его минимаксной стратегией.

Принцип осторожности, диктующий игрокам выбор соответствующих стратегий (максиминной и минимаксной), является в теории игр основным принципом и называется принципом минимакса.

Седловая точка в игре имеет место тогда, когда наблюдается равенство:

a = b.

В платежной матрице такой игры существует элемент, являющийся одновременно минимальным в своей строке и максимальным в своем столбце. Такой элемент называют седловой точкой. При этом значение n = a = b называют чистой ценой игры. В этом случае решение игры (совокупность оптимальных стратегий игроков) обладает следующим свойством: если один из игроков придерживается своей оптимальной стратегии, то для другого не может быть выгодным отклоняться от своей оптимальной стратегии. Поэтому для игры с седловой точкой минимаксные стратегии обладают устойчивостью.

Критерием Вальда "рассчитывай на худшее" (критерий крайнего пессимизма) называют критерий, предписывающий обеспечить значение параметра эффекта, равного а. Напомним:

.

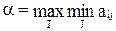Этот критерий ориентирует лицо, принимающее решение, на наихудшие условия и рекомендует выбрать ту стратегию, для который выигрыш максимален. В других, более благоприятных условиях использование этого критерия приводит к потере эффективности системы или операции.

Критерий минимаксного риска Сэвиджа При его использовании обеспечивается наименьшее значение максимальной величины риска:

,

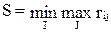где риск r_ij определяется выражением:

,

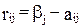где b_j – максимально возможный выигрыш игрока при состоянии природы П_j (или стратегии противника с номером j), т. е.:

.

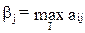Критерий Сэвиджа. как и критерий Вальда. – это критерий крайнего пессимизма, но только пессимизм здесь проявляется в том, что минимизируется максимальная потеря в выигрыше, по сравнению с тем. чего можно было бы достичь в данных условиях.

Критерий пессимизма – оптимизма Гурвица. Этот критерий рекомендует при выборе решения в условиях неопределенности не руководствоваться ни крайним пессимизмом (всегда рассчитывай на худшее), ни оптимизмом (все будет наилучшим образом). Рекомендуется некое среднее решение. Этот критерий имеет вид:

,

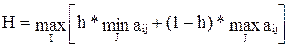где

h – некий коэффициент, выбираемый экспертно из интервала между 0 и 1.

Использование этого коэффициента вносит дополнительный субъективизм в принятие решений с использованием критерия Гурвица.

В целом теория игр может рассматриваться как интересный методический инструмент для анализа ситуаций, характеризующихся конфликтом сторон и неопределенностью.

Однако в связи с отмеченными выше существенными ограничениями, лежащими в основе формализации игры:

1) далеко не все реальные ситуации допускают такую формализацию;

2) полученные выводы в реальных ситуациях выглядят, зачастую, банальными (например, направить все ресурсы на наиболее эффективные операции) и могут требовать корректировки с позиций здравого смысла, диверсификации видов деятельности и т.д. Это снижает практическую эффективность игрового подхода в реальной деятельности.