КВАНТОВАЯ МЕТРОЛОГИЯ
В начале XX века немецкий физик М. Планк показал, что основные единицы для нашей Вселенной, однозначно предопределенные наиболее общими законами физики, могут быть составлены из фундаментальных физических констант:
скорости света с, постоянной Планка ђ и гравитационной постоянной γ. Значения этих констант, фигурирующих в виде коэффициентов в уравнениях основных физических теорий — классической и квантовой электродинамике и общей теории относительности — являются максимально стабильными и не зависящими от внешних условий. Однако планковские единицы длины, времени и массы 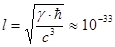 см,
см, 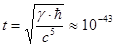 c,
c, 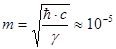 г лежат очень далеко от используемых на практике диапазонов. Кроме того, значение гравитационной постоянной до сих пор известно с недостаточной точностью (это же в меньшей мере относится и к ђ ) . Но самым главным недостатком планковских единиц является то, что мы не располагаем реальными физическими процессами, в которых бы они воспроизводились. В частности, науке пока не известны объекты, которые имели бы в точности планковскую массу, планковские размеры или длились бы планковское время. Именно поэтому планковские единицы, несмотря на их универсальность, в метрологии в настоящее время не используются.
г лежат очень далеко от используемых на практике диапазонов. Кроме того, значение гравитационной постоянной до сих пор известно с недостаточной точностью (это же в меньшей мере относится и к ђ ) . Но самым главным недостатком планковских единиц является то, что мы не располагаем реальными физическими процессами, в которых бы они воспроизводились. В частности, науке пока не известны объекты, которые имели бы в точности планковскую массу, планковские размеры или длились бы планковское время. Именно поэтому планковские единицы, несмотря на их универсальность, в метрологии в настоящее время не используются.
Реальная возможность создания универсальной системы естественных мер появилась после открытия так называемых макроскопических квантовых эффектов: сверхпроводимости, сверхтекучести, квантового эффекта Холла. В этих эффектах в результате когерентного поведения огромного числа микрочастиц происходит квантование строго определенными порциями той или иной макроскопической величины. Рассмотрим, в частности, эффект Джозефсона, который возникает в контактах двух сверхпроводников, разделенных тонким слоем диэлектрика.
Как известно, электроны в вакууме отталкиваются друг от друга по закону Кулона. В твердом теле, помимо электронов, имеются положительно заряженные ионы решетки. Притягиваясь к электронам, они экранируют их заряд. В некоторых веществах при достаточно низких температурах суммарное взаимодействие электронов может соответствовать слабому притяжению. В этом случае электроны объединяются в так называемые куперовские пары. Такие пары, в отличие от отдельных электронов, имеют нулевой спин (т. е. подчиняются статистике Бозе). Это позволяет большому числу пар скапливаться в одном и том же квантовом состоянии. Если средняя скорость куперовских пар отлична от нуля, т. е. существует незатухающий электрических ток, то говорят, что имеет место явление сверхпроводимости.
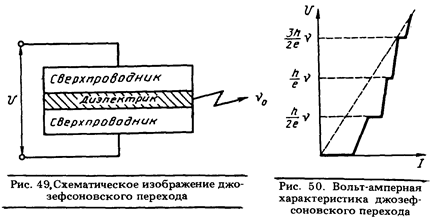
Предположим теперь, что два сверхпроводника разделены очень тонкой пленкой диэлектрика (см. рис. 49). Куперовские пары могут просачиваться (туннелировать) через диэлектрик из одного сверхпроводника в другой. При этом, если фазы волновых функций пар в двух сверхпроводниках окажутся различными, то через переход Джозефсона будет течь ток в отсутствие разности потенциалов. Такое явление получило название стационарного эффекта Джозефсона.
Если приложить к двум сторонам джозефсоновского перехода разность потенциалов U, то при туннелировании куперовской пары из одного сверхпроводника в другой избыток ее энергии 2eU излучается в виде кванта света—фотона. Частота no этого кванта определяется законом сохранения энергии:
h vo =2 е U.
Это явление называется, нестационарным эффектом Джозефсона.
Если, наоборот, облучать джозефсоновскии переход излучением с частотой v, то при совпадении этой частоты с характерной для данного напряжения U частотой vo возникает резонансное взаимодействие. Такой же резонанс наступает и при v = vo/n, где п — любое целое число, в результате чего на вольт-амперной характеристике перехода появляются особенности (см. рис. 50) в виде ступенек при напряжениях
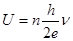
Заряд электрона е является такой же фундаментальной физической константой, как и упоминавшиеся выше h, с, g. Величина h/2e называется квантом магнитного потока, значение которого определяется с большей точностью, чем значения h и е по отдельности. Поскольку частота в настоящее время является наиболее точно измеряемой величиной (числовое значение стандартного отклонения не превышает 10-13) точность воспроизведения напряжения с помощью эффекта Джозефсона ограничивается точностью значения h/2e. Стандартное отклонение при воспроизведении U . составляет в настоящее время ~ 10-8 В.
На использовании эффекта Джозефсона основаны эталоны единицы напряжения — вольта во всех промышленно развитых странах с начала 1980-х гг. В состав эталона обычно входит дискретный переход, возбуждаемый СВЧ излучением на частоте 8 ... 10 ГГц. Значение квантованного напряжения составляет при этом U = 4 . . . 10 мВ. Столь низкое значение воспроизводимого напряжения вынуждает включать в состав эталона масштабные- преобразователи напряжения различной конструкции и нормальные элементы, приводящие к потере точности. В связи с этим, в самое последнее время были созданы интегральные схемы, включающие в себя порядка 1000 переходов Джозефсона и позволяющие воспроизводить напряжение непосредственно в 1 В и выше.
Из общефизических соображений и проведенных экспериментов следует, что стабильность эталонов на основе эффекта Джозефсона может достигать ~ 1016, что открывает широкие перспективы для совершенствования естественного эталона вольта.
Не менее интересные возможности для метрологии дает открытый в 1980 г. фон-Клитцингом квантовый эффект Холла. Суть его состоит в том, что в специальных структурах типа металл — диэлектрик — полупроводник при температуре жидкого гелия и в сильном магнитном поле электрическое сопротивление принимает строго фиксированные дискретные значения
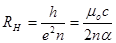
где mo — магнитная постоянная вакуума; a = mo ce2 /2h — постоянная тонкой структуры.
Рассмотрим схему наблюдения квантового эффекта Холла (см. рис. 51). Пусть на металлическую пластину подается положительное напряжение UВ . Тогда часть электронов из кремниевого полупроводника Si подтянется к границе диэлектрика SiO2; и окажется заключенной в тонком слое — канале, ограниченном на рис. 51, а пунктиром. Действительно, диэлектрик SiO2 для электронов непроницаем, а обратно в полупроводник Si им не дает вернуться притяжение к металлической пластине.
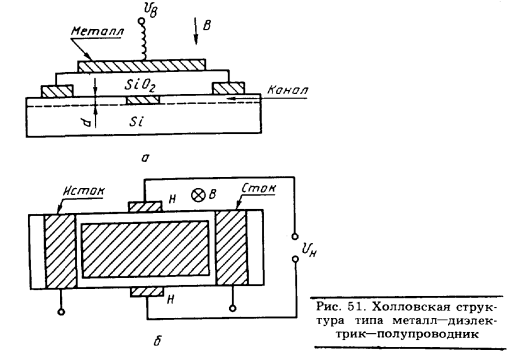
Запертые в канале толщиной d электроны, согласно квантовой механике, будут занимать наинизший из возможных дискретных энергетических уровней, соответствующих движению поперек слоя, а их волновые функции будут размазаны по толщине канала. Такие электроны различаются между собой величиной и направлением импульса в плоскости канала, т. е. становятся как бы двумерными.
Если подать некоторое напряжение на электроды ,,исток" — „сток" (см. рис. 51, б), то между ними потечет ток I.
Если, кроме того, приложить магнитное поле В, перпендикулярное плоскости канала, то электроны, изгибая свои траектории в поле В, начнут скапливаться у боковых краев структуры, пока возникшая разность потенциалов UH между хол-ловскими контактами H не воспрепятствует их дальнейшему накоплению. Это классический эффект Холла, характеризуемый холловским сопротивлением RH = UH /I. Как показано в курсе общей физики, величина RH обратно пропорциональна плотности электронов в канале.
Существенно новая ситуация возникает при учете квантового характера движения электронов в магнитном поле. Согласно квантовой механике, энергия их движения в плоскости слоя может принимать только дискретные значения
En = (п + 1/2) ħe B/me с,
где п = 0,1,2, ... .
Таким образом, движение электрона оказывается квантованным по всем трем координатам. Следствием этого является наличие на зависимости RH от плотности электронов в слое pe плоских участков — плато с квантованными значениями RH, согласно приведенной выше формуле (см. рис. 52). На практике величину рe регулируют, изменяя UB.
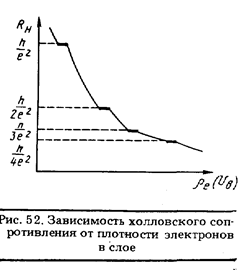
Качественное объяснение данного явления, открытого фон Клитцингом в 1980 г. и названного квантовым эффектом Холла, связано с наличием в слое примесей. Расчет показывает, что в некотором диапазоне увеличения концентрации электронов рe добавочные электроны оказываются связанными около примесей и не дают вклада в ток. На графике зависимости RH от рe именно этим диапазонам и соответствуют плато. Например, при п = 4холловское сопротивление составляет 6453,2 Ом и имеет воспроизводимость 108.
В настоящее время строгая количественная теория квантового эффекта Холла еще не построена и неизвестно, каких предельных точностей воспроизведения единицы сопротивления можно достичь с его помощью. Однако уже полученные экспериментальные результаты делают этот метод воспроизведения сопротивления предпочтительным по сравнению
с другими, и во всех развитых странах, в том числе в СССР, ведется активная подготовка к переходу на квантовый эталон сопротивления.
Недавно японскими физиками открыт новый макроскопический квантовый эффект, возникающий на одном джозефсоновском переходе малой емкости или на гранулярной сверх-проводящей пленке, в которой образуется решетка таких переходов. Облучение такого образца электромагнитными колебаниями с частотой v приводит к появлению резонансных пиков на его вольт-амперной характеристике, что означает квантование постоянного тока, проходящего через образец, согласно соотношению
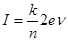
где k, n — целые числа. С использованием этого эффекта после его детального исследования можно будет, по-видимому, создать естественный эталон единицы силы тока.
Что же принципиально нового вносят в метрологию эталоны, основанные на макроскопических квантовых эффектах? Во-первых,это подлинно естественные эталоны. При выполнении определенных условий, которые можно строго фиксировать (тип и качество структуры, температура, магнитное поле и т. д.), они воспроизводят единицы, размеры которых выражаются через значения фундаментальных физических констант, общие для всей Вселенной. Во-вторых,широкое их применение открывает возможность децентрализованного воспроизведения единиц и упразднения неэффективной и дорогостоящей системы передачи информации об их размерах средствам измерений.
Из сказанного следует важность определения точного значения фундаментальных физических, констант. Работы в этом направлении ведутся многими лабораториями мира. Международная организация КОДАТА (Комитет по численным данным для науки и техники) проводит математическую обработку и согласование получаемых данных. Рекомендованные значения фундаментальных констант публикуется для использования всеми специалистами, имеющими дело с точными измерениями. В табл. 16 приведены значения наиболее часто встречающихся фундаментальных физических констант и их комбинаций по результатам согласования 1986 г.
Приведенное в первой строчке таблицы значение скорости света постулировано как точное и используется при определении размера единицы длины в едином эталоне времени, частоты и длины. В сентябре 1988 г. в Париже состоялось заседание Международного консультативного комитета по электричеству, на котором было принято решение постулировать как точное и значение 2е/ħ = 483597,9 ГГц/В. Благодаря этому соглашению, точность поддержания размера единицы напряжения с помощью эффекта Джозефсона может быть значительно повышена.
Таблица 16
| Величина | Обозначение | Значение | Единица | Относитель-ное стандартное отклонение, 10-6 Х 10"6 |
| Скорость света в вакууме | с | мс-1 | - | |
| Гравитационная постоянная | g | 6,67259 ×10-11 | м3 × кг-1Х Хс-2 | |
| Постоянная Планка | 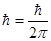
| 1,05457266 × 10-34 | Дж-с | 0,60 |
| Заряд электрона | е | 1,60217733 × 10-19 | Кл | 0,30 |
| Квант магнитного потока | ħ/2e | 2,06783461 ×10-15 | Вб | 0,30 |
| Масса электрона | mе | 9.1093897 ×10-31 | кг | 0,59 |
| Постоянная тон- кой структуры | a | 7,29735308 × 10-3 | - | 0,045 |
| Постоянная Аво- гадро | NА | 6,0221367×1023 | моль-1 | 0,59 |
| Постоянная фон- Клитцинга | ħ/e2 | 25812,8056 | Ом | 0.045 |
Из рассмотренных в этом разделе естественных эталонов один лишь эталон ома воспроизводит размер единицы, который выражается исключительно через значения фундаментальных физических констант. Размеры единиц, воспроизводимые другими естественными эталонами (вольта, ампера, метра), выражаются не только через значения фундаментальных физических констант, но и через единицу частоты, размер которой должен воспроизводиться независимо. Вычислить его через значения фундаментальных физических констант невозможно, так как в едином эталоне единиц времени, частоты и длины атомы цезия-133 являются сложными многоэлементными системами, и решение уравнений квантовой теории, из которых определяется частота их квантовых переходов, не под силу даже самым мощным ЭВМ. Между тем, в идеале система естественных эталонов должна быть такой, чтобы размеры всех воспроизводимых единиц выражались только через значения фундаментальных физических констант. Это возможно» если взять, например, в качестве эталонной частоту двухфотонного оптического перехода Is-2s в водороде, измеряемую методами бездопплеровской лазерной спектроскопии. Стандартное отклонение частоты этого перехода, вычисляемой через значения фундаментальных физических констант, не превышает 10-12 Гц.
Наибольшую трудность представляет создание естественного эталона единицы массы. Природный масштаб этой единицы, как уже отмечалось, задаётся массой микрообъектов (например, атомов). Он очень мал, а переход к массе макрообъектов осуществляется с помощью фундаментальной физической константы — числа Авогадро, значение которой известно не настолько точно, чтобы обеспечить воспроизведение единицы массы — килограмма — со стандартным отклонением порядка 10-8 кг. Эта проблема ждет своего решения.
Дата добавления: 2015-02-05; просмотров: 3433;
