Выбор пропускных способностей

Увеличение пропускных способностей уменьшает среднюю задержку в сети, но увеличивает стоимость, и это является основной особенностью задачи оптимизации. Для каждой линии имеется зависимость между ее стоимостью (зависящей также от длины) и пропускной способностью С. Для каждого канала i имеем поток l _i; C_i- пропускная способность этого канала, а d_iC_i - его стоимость. Предположим также, что задержка в сети зависит только от полного потока в каналах. Величины l _i и d_i считаются заданными, а C_i необходимо найти.

Определение средней задержки T требует анализа сложной системы массового обслуживания. Для получения простой формулы для T делается ряд предположений. Во-первых, все очереди связываются с линиями, выходящими из узла. С каждой i-й линией сопоставляется средняя задержка на этой линии. Пусть g - общий трафик в сети. Тогда среднее число пакетов, находящихся в сети, есть g T (T - средняя задержка пакета). С другой стороны, число пакетов в каждой очереди из тех же соображений есть l _iT_i, откуда g T= å l _iT_i.

Поскольку время обслуживания пропорционально длине пакета, необходимо ввести еще один параметр m, характеризующий среднюю длину пакета. В очередь на передачу поступают как пакеты, пришедшие из других линий, так и вновь поступившие в сеть. Эти потоки пакетов вышли из разных очередей, и поэтому интервалы между поступлениями отдельных пакетов распределены по весьма сложному закону. Если очереди представить с помощью СМО М/М/1 (что оправдывается на практике) и учесть формулу для средней задержки в этой системе T_i=1/(m C_i-l _i), то для средней задержки во всей сети, которую необходимо минимизировать, получаем:

T=å (l _i/g )[1/(m C_i-l _i )].

В этом выражении не учтены время обработки пакета в узле и задержки при распространении сигнала по линии связи, а также наличие пакетов подтверждения и другой служебной информации, передаваемой по сети.

Поиск минимума времени T и соответствующих ему значений C_i осуществляется с помощью метода неопределенных множителей Лагранжа. Распределение пропускных способностей каналов, получающихся из уравнений, оказывается равным

C_i=l _i/m +k .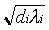

Первое слагаемое есть минимальная пропускная способность, а второе пропорционально квадратному корню из величины потока.

Итак, для задач оптимального распределения пропускных способностей удалось получить точное аналитическое решение, хотя и после введения большого числа упрощающих предположений.